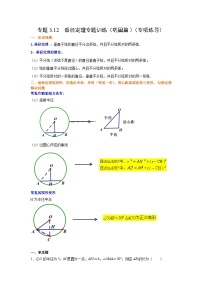
北师大版九年级数学下册 专题3.11 垂径定理专题训练（基础篇）（专项练习）（附答案）

这是一份北师大版九年级数学下册 专题3.11 垂径定理专题训练（基础篇）（专项练习）（附答案），共34页。试卷主要包含了知识回顾，填空题，解答题等内容，欢迎下载使用。

1.垂径定理 ：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧.
2、垂径定理的推论：
平分弦（该弦不是直径）的直径垂直于弦，并且平分弦所对的两条弧；
弦的垂直平分线经过圆心，并且平分弦所对的两条弧；
平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧.
垂径定理的应用：构造由半径、半弦（弦的一半）、弦心距组成直角三角形，勾股定理解决问题
常见作辅助线方法有：
连接半径

过圆心作弦的垂线
常见的图形变形
H为半径中点
一、单选题
1．如图，为的直径，弦，垂足为，，，则的半径为（ ）
A．3B．4C．5D．无法确定
2．如图，半圆的直径，为圆心，为的中点，，交于点，则弦的长为（ ）
A．B．C．D．
3．如图，是的直径，弦于点，，，则的长为（ ）
A．4B．5C．8D．16
4．如图，是的直径，弦于点E，，的半径为6，则弦的长为（ ）
A．6B．C．3D．6
5．已知：如图，是的直径，弦交于E点，，则的长为（ ）
A．B．C．D．4
6．如图，是的直径，将一块直角三角板的角的顶点与圆心O重合，角的两边分别与交于E、F两点，若点F是弧的中点，的半径是4，则弦的长为（ ）
A．B．C．6D．
7．如图，拱桥可以近似地看作直径为250m的圆弧，桥拱和路面之间用数根钢索垂直相连，其正下方的路面AB长度为150m，那么这些钢索中最长的一根的长度为（ ）
A．50mB．40mC．30mD．25m
8．如图，是的直径，弦于点，，，则的长是（ ）
A．B．C．D．
9．如图，在中，直径，垂足为M．若，则的半径为（ ）
A．0.2B．2.6C．2.4D．4
10．往直径为52cm的圆柱形容器内装入一些水以后，截面如图所示，若水面宽，则水的最大深度为（ ）

A．8cmB．10cmC．14cmD．16cm
二、填空题
11．如图，一圆弧过方格的格点A、B、C，在方格中建立平面直角坐标系，使点A的坐标为（0，3），则该圆弧所在圆的圆心坐标是______．
12．如图，将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长为_____．
13．如图，是的直径，弦于点，且，则的半径为__________．
14．如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB=8，CD=6，则BE=______．
15．《九章算术》是我国古代数学成就的杰出代表作，其中《方田》章计算弧田面积所用的经验公式是：弧田面积（弦×矢+矢2）．孤田是由圆弧和其所对的弦围成（如图中的阴影部分），公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差，运用垂径定理（当半径⊥弦时，平分）可以求解．现已知弦米，半径等于5米的弧田，按照上述公式计算出弧田的面积为_____平方米．
16．和平中学自行车停车棚顶部的剖面如图所示，已知AB＝16m，半径OA＝10m，高度CD为____m．
17．如图，以点P为圆心的圆弧与x轴交于A，B两点，点P的坐标为(4，2)，点A的坐标为(2，0)，则点B的坐标为______．
18．如图，在⊙O中，弦的长为4，圆心到弦的距离为2，则的度数为______．
19．如图，CD是⊙O的直径，弦AB⊥CD于点H，若∠D=30°，CH=1cm，则AB=
_________ cm．
20．如图所示，半径为的内两条相互垂直的弦，交于点，，，则=______.

21．如图，AB为⊙O的直径，弦CD⊥AB于点E，已知CD＝6，EB＝2，则⊙O的半径为_____．
22．“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何”此问题的实质就是解决下面的问题：“如图，CD为⊙O的直径，弦AB⊥CD于点E，CE=1，AB=10，求CD的长”．根据题意可得CD的长为______．
23．已知的半径为，弦，是上任意一点，则线段的最小值为_____．
24．如图，AD是⊙O的直径，弦BC⊥AD于E，AB=BC=12，则OC=______．
25．如图，是的直径，弦，垂足为点H．若，，则的半径长为____________．
26．如图，将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心，则折痕AB的长为________．

27．如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB=10，CD=8，则BE=_____．

28．当宽为3cm的刻度尺的一边与圆相切时，另一边与圆的两个交点处的读数如图所示（单位：cm），那么该圆的半径为_______cm．
29．如图，在平面直角坐标系中，点A（0，1）、B（0，﹣1），以点A为圆心，AB为半径作圆，交x轴于点C、D，则CD的长是____．
30．如图，点A，B是⊙O上两点，AB=10，点P是⊙O上的动点（P与A，B不重合），连接AP，PB，过点O分别作OE⊥AP于E，OF⊥PB于F，则EF=_____________．

31．如图，⊙O的半径为5，点P是弦AB延长线上的一点，连接OP，若OP=8，∠P=30°，则弦AB的长为___．

32．如图，AB、CD是半径为5的⊙O的两条弦，AB=8，CD=6，MN是直径，AB⊥MN于点E，CD⊥MN于点F，P为EF上的任意一点，则PA+PC的最小值为______．
33．如图，的直径，弦，垂足为，，则的长为______．
34．如图是一个隧道的横截面，它的形状是以点O为圆心的圆的一部分，若M是⊙O中弦CD的中点，EM经过圆心O交⊙O于点E，并且CD=8，EM=8，则⊙O的半径为_________．
35．如图，，在射线AC上顺次截取，，以为直径作交射线于、两点，则线段的长是__________cm．
三、解答题
36．如图，⊙O是△ABC的外接圆，AB是⊙O的直径，D为⊙O上一点，OD⊥AC，垂足为E，连接BD．
(1)求证：BD平分∠ABC；
(2) 当∠ODB=30°时，求证：BC=OD．
37．如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB＝8，CD＝2．
（1）求OD的长．
（2）求EC的长．
38．如图，⊙O中，直径CD⊥弦AB于E，AM⊥BC于M，交CD于N，连AD．
（1）求证：AD=AN；
（2）若AE=，ON=1，求⊙O的半径．
参考答案
1．C
【分析】连接OA，由垂径定理得AE=3，设OA=OC=x，根据勾股定理列出方程，进而即可求解．
解：连接OA，
∵为的直径，弦，
∴AE=AB=3，
设OA=OC=x，则OE=x-1，
∴，解得：x=5，
∴的半径为5．
故选C．
【点拨】本题主要考查垂径定理和勾股定理，添加辅助线，构造直角三角形是解题的关键．
2．A
【分析】连接，利用垂径定理和勾股定理求解即可得到答案．
解：如图所示，连接，
∵，，
∴，
∴，即．
∵，
∴，
∵为的中点，
∴，
在中，，，
∴，
∴．
故选A．
【点拨】本题主要考查了垂径定理和勾股定理，解题的关键在于能够熟练掌握相关知识进行求解．
3．C
【分析】根据垂径定理得出CM=DM，再由已知条件得出圆的半径为5，在Rt△OCM中，由勾股定理得出CM即可，从而得出CD．
解：∵AB是⊙O的直径，弦CD⊥AB，
∴CM=DM，
∵AM=2，BM=8，
∴AB=10，
∴OA=OC=5，
在Rt△OCM中，OM2+CM2=OC2，
∴CM==4，
∴CD=8．
故选：C．
【点拨】本题考查了垂径定理，圆周角定理以及勾股定理，掌握定理的内容并熟练地运用是解题的关键．
4．D
【分析】连接，根据垂径定理可得，由，可得，进而证明，可得，进而可得为等边三角形，进而求得，即可求得．
解：连接，如图，
是的直径，弦
又
为等边三角形，
故选D
【点拨】本题考查了垂径定理，全等三角形的性质与判定，等边三角形的性质，勾股定理，添加辅助线证明是解题的关键．
5．A
【分析】如图，过点作于，根据已知条件求得勾股定理求得，由垂径定理可得，进而可得的长．
解：如图，过点作于，
则，
，
，
，
，
，
，
，
．
故选A．
【点拨】本题考查了垂径定理，含30度角的直角三角形的性质，勾股定理，作出辅助线是解题的关键．
6．A
【分析】设DE交OB于点M，根据F为弧DE中点，得出∠AOF=∠FOD=60°，OF⊥DE，可求出DE=2DM，求出∠EDO=∠DEO=30°，求出OM，即可求出DM，即可求解．
解：如图，设DE交OB于点M，
∵点F是弧的中点，
∴∠AOF=∠DOF=60°，OF⊥DE，
∴DE=2DM，
∴∠EDO=∠DEO= （180°-60°-60°）=30°，
∵的半径是4，
∴OM= OD=2，
在 中，由勾股定理得：
，
∴DE=2DM= ．
故选：A．
【点拨】本题考查了垂径定理，勾股定理，含30度角的直角三角形，三角形的内角和定理，等腰三角形的性质的应用，熟练掌握相关知识点是解题的关键．
7．D
【分析】设圆弧的圆心为O，过O作OC⊥AB于C，交于D，连接OA，先由垂径定理得AC＝BC＝AB＝75m，再由勾股定理求出OC＝100m，然后求出CD的长即可．
解：设圆弧的圆心为O，过O作OC⊥AB于C，交于D，连接OA，
则OA＝OD＝×250＝125（m），AC＝BC＝AB＝×150＝75（m），
∴OC＝＝＝100（m），
∴CD＝OD﹣OC＝125﹣100＝25（m），
即这些钢索中最长的一根为25m，
故选：D．
【点拨】本题考查了垂径定理和勾股定理等知识；熟练掌握垂径定理和勾股定理是解题的关键．
8．A
【分析】由垂径定理可得的长度，再由勾股定理可得的长度，然后由即可得出的长度．
解：弦于点，cm，
cm，
在中，cm，
（cm），
cm，
故选：A．
【点拨】本题考查了垂径定理以及勾股定理，利用垂径定理结合勾股定理求出的长度是解题的关键．
9．B
【分析】连接OC，设⊙O的半径为R，则OC=R，OM=5-R，根据垂径定理求出CM，根据勾股定理得出方程，求出即可．
解：连接OC，设⊙O的半径为R，则OC=R，OM=5-R，
∵直径EF⊥CD，垂足为M，CD=2，
∴CM=DM=1，
在Rt△OMC中，由勾股定理得：OC2=OM2+CM2，
R2=（5-R）2+1²，
解得R=2.6．
故选：B．
【点拨】本题考查了勾股定理，垂径定理的应用，用了方程思想，题目比较典型，难度适中．
10．D
【分析】连接OB，过点O作OC⊥AB于点D，交⊙O于点C，先由垂径定理求出BD的长，再根据勾股定理求出OD的长，进而可得出CD的长．
解：连接OB，过点O作OC⊥AB于点D，交⊙O于点C，如图所示：
∵AB=48cm，
∴BD=AB=×48=24（cm），
∵⊙O的直径为52cm，
∴OB=OC=26cm，
在Rt△OBD中，（cm），
∴CD=OC-OD=26-10=16（cm），
故选：D．
【点拨】本题考查了垂径定理、勾股定理等知识；根据题意作出辅助线，构造出直角三角形是解答此题的关键．
11．．
【分析】直接利用垂径定理推论得出圆心位置，进而利用点坐标得出原点位置即可得出答案．
解：如图示，∵点A的坐标为（0，3），
据此建立平面直角坐标系如下图所示，
连接，，作，的中垂线，交点是点
则，该圆弧所在圆的圆心坐标是：．
故答案是：．
【点拨】本题主要考查了垂径定理以及坐标与图形的性质，正确得出圆心位置是解题关键．
12．
【分析】过点作交于点,连接，由折叠的性质可知：，根据勾股定理可求出的长，再由垂径定理可得;即可得出答案．
解：
如图所示，过点作于，连接，
，，，
在中，由勾股定理得：，
由垂径定理得：．
故答案为：．
【点拨】本题考查了垂径定理和勾股定理的应用，正确应用勾股定理是解题的关键．
13．
【分析】根据垂径定理得出CE=DE，再由勾股定理得出OD2=DE2+（AE-OA）2，代入求解即可．
解：∵CD⊥AB，
∴CE=DE=CD，
∵AE=CD=6，
∴CE=DE=3，
∵OD=OB=OA，OE=AE-OA，
在Rt△ODE中，由勾股定理可得：OD2=DE2+（AE-OA）2，
即：OD2=32+（6-OD）2，
解得：OD=，
∴⊙O的半径为：，
故答案为：．
【点拨】本题考查了垂径定理、勾股定理等知识；熟练掌握垂径定理和勾股定理是解题的关键．
14．4-
解：试题解析：如图，连接OC.
∵弦CD⊥AB于点E，CD=6，

∵在中,


故答案为:
15．10
【分析】根据垂径定理得到，由勾股定理得到，求得，根据弧田面积（弦×矢+矢2）即可得到结论．
解：∵弦米，半径弦，
∴，
∴，
∴，
∴弧田面积（弦×矢+矢2），
故答案为10
【点拨】此题考查垂径定理的应用，关键是根据垂径定理和扇形面积解答．
16．4．
【分析】由CD⊥AB，根据垂径定理得到AD＝DB＝8，再在Rt△OAD中，利用勾股定理计算出OD，则通过CD＝OC−OD求出CD．
解：∵CD⊥AB，AB＝16，
∴AD＝DB＝8，
在Rt△OAD中，AB＝16m，半径OA＝10m，
∴OD＝＝6，
∴CD＝OC﹣OD＝10﹣6＝4（m）．
故答案为4．
【点拨】本题考查了垂径定理：垂直于弦的直径平分弦，并且平分弦所对的弧．也考查了切线的性质定理以及勾股定理．
17．(6,0)
解：过点P作PM⊥AB于M，则M的坐标是（4，0）
∴MB=MA=4-2=2，
∴点B的坐标为(6,0)
18．
【分析】先根据垂径定理可得，再根据等腰直角三角形的判定与性质即可得．
解：由题意得：，，
，
，
，
是等腰直角三角形，
，
故答案为：．
【点拨】本题考查了垂径定理、等腰直角三角形的判定与性质，熟练掌握垂径定理是解题关键．
19．
解：连接AC、BC，则∠CAH=30°， AC=，根据勾股定理AH=，故AB=
20．.
【解析】
【分析】作OM⊥AB于M，ON⊥CD于N，连接OP，OB，OD，先求出OM，ON，进而证得四边形OMPN是矩形，所以OP=PM，利用勾股定理可以求出OP的长．
解：作OM⊥AB于M，ON⊥CD于N，连接OP，OB，OD，
由垂径定理得：
∵弦AB、CD互相垂直，
∴∠DPB=90°，
∵OM⊥AB于M，ON⊥CD于N，
∴∠OMP=∠ONP=90°
∴四边形MONP是矩形，

故答案为：
【点拨】本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
21．
【分析】连接OC，可知，点E为CD的中点，设⊙O的半径为xcm，在Rt△OEC中，OE=OB-BE=x-2，根据勾股定理，求得x值即可．
解：连接OC，
∵AB为⊙O的直径，AB⊥CD，
∴CE＝DE＝CD＝×6＝3，
设⊙O的半径为xcm，
则OC＝xcm，OE＝OB﹣BE＝x﹣2，
在Rt△OCE中，OC2＝OE2+CE2，
∴x2＝32+（x﹣2）2，
解得：x＝，
∴⊙O的半径为，
故答案为．
【点拨】本题考查了垂径定理、勾股定理，正确添加辅助线构造直角三角形是解题的关键.
22．26
解：试题分析：连接OA，AB⊥CD，由垂径定理知，点E是AB的中点，AE=AB=5，OE=OC﹣CE=OA﹣CE，
设半径为r，由勾股定理得，OA2=AE2+OE2=AE2+（OA﹣CE）2，即r2=52+（r﹣1）2，
解得：r=13，所以CD=2r=26，即圆的直径为26．
【考点】垂径定理的应用．
23．4
【分析】由点到直线的距离，垂线段最短，连接作ON⊥AB，直接利用垂径定理得出AN的长，再结合勾股定理得出答案．
解：连接 作ON⊥AB，

根据垂径定理，AN=AB=×6=3，
根据勾股定理，ON=，
即线段OM的最小值为：4．
故答案为：4．
【点拨】本题考查了点到直线的距离，垂线段最短，垂径定理，勾股定理的应用，掌握以上知识是解题关键．
24．4
解：试题解析：如图，连接BD；
∵直径AD⊥BC，
∴BE=CE=BC=6；
由勾股定理得：
AE=；
∵AD为⊙O的直径，
∴∠ABD=90°；
由射影定理得：
AB2=AE•AD
∴AD==
∴OC=AD=.
考点：垂径定理.
25．13
【分析】连接，先根据垂径定理可得，再在中，利用勾股定理即可得．
解：如图，连接，
是的直径，弦，，
，
设的半径长为，则，
，
，
在中，，即，
解得，
即的半径长为13，
故答案为：13．
【点拨】本题考查了垂径定理、勾股定理，熟练掌握垂径定理是解题关键．
26．cm
【分析】在图中构建直角三角形，先根据勾股定理得AD的长，再根据垂径定理得AB的长即可．
解：如图：作OD⊥AB于D，连接OA．
根据题意得：OD＝OA＝1cm，
再根据勾股定理得：AD＝＝＝cm，
由垂径定理得：AB＝2cm．
故答案为：cm．
【点拨】本题考查了垂径定理，根据题意构造垂径、应用勾股定理是解答本题的关键.
27．2
【分析】根据垂径定理得到CE =CD=4，再利用勾股定理计算出OE，然后计算OB与OE的差即可．
解：连接OC
∵弦CD⊥AB，CD=8，
∴CE=CD=4，
在Rt△OCE中，
∵OC=5，CE=4，
由勾股定理得，
∴OE=，
∴BE=OB−OE=5−3=2．
故答案为：2．
【点拨】本题考查了垂径定理和勾股定理.利用垂径定理求出CE的长，再利用勾股定理求出OE的长是解题的关键．
28．．
解：如图，连接OA，过点O作OD⊥AB于点D，
∵OD⊥AB，∴AD=AB=（9﹣1）=4．
设OA=r，则OD=r﹣3，
在Rt△OAD中，
OA2﹣OD2=AD2，即r2﹣（r﹣3）2=42，解得r=（cm）．
29．
【分析】根据题意在中求出，利用垂径定理得出结果．
解：由题意，在中，，，
由垂径定理知，，
故答案为：．
【点拨】本题考查了勾股定理及垂径定理，熟练掌握垂径定理是解决本题的关键．
30．5.
解：试题解析：点P是⊙O上的动点（P与A，B不重合），但不管点P如何动，因为OE⊥AP于E，OF⊥PB于F，根据垂径定理，E为AP中点，F为PB中点，EF为△APB中位线．根据三角形中位线定理，EF=AB=×10=5．
考点：1.垂径定理；2.三角形中位线定理．
31．6
【解析】试题解析：作OC⊥AB于C，连结OA，如图，
则AC=BC，
∵OP=8，∠APO=30°，
∴OC=4，
在Rt△OAC中，OA=5，OC=4，
∴AC=3，
∴AB=2AC=6．
32．
【解析】
【分析】由于A、B两点关于MN对称，因而PA+PC=PB+PC，即当B、C、P在一条直线上时，PA+PC的最小，即BC的值就是PA+PC的最小值.
解：连接OA，OB，OC，作CH垂直于AB于H．
∵AB=8，CD=6，MN是直径，AB⊥MN于点E，CD⊥MN于点F，
∴BE=AB=4，CF=CD=3，
∴OE===3,
OF===4,
∴CH=OE+OF=3+4=7，
BH=BE+EH=BE+CF=4+3=7，
在Rt△BCH中根据勾股定理得到BC===.
故答案为：.
【点拨】本题考查的是轴对称-最短路线问题及垂径定理、勾股定理．根据题意作出辅助线，构造出直角三角形是解答此题的关键．
33．24
【分析】连接，先根据求出的长，再在中，利用勾股定理可得的长，然后利用垂径定理即可得．
解：如图，连接，
的直径，
，
，，
，
，
，
故答案为：24．
【点拨】本题考查了勾股定理、垂径定理，熟练掌握垂径定理是解题关键．
34．5
【分析】根据垂径定理得EM⊥CD，则CM=DM=4，在Rt△COM中，由勾股定理得OC2=CM2+OM2，进而可求得半径OC即可．
解：连接OC，如图所示：
∵M是⊙O弦CD的中点，CD=8，
∴EM⊥CD，CM=DM=CD=4，
设⊙O的半径为x ，
在Rt△COM中，由勾股定理得：OC2=CM2+OM2，
即：x2=42+(8-x)2，
解得：x=5，
即⊙O的半径为5，
故答案为：5．
【点拨】本题主要考查了垂径定理的应用，勾股定理等知识；熟练掌握垂径定理，由勾股定理得出方程是解题的关键．
35．6
【分析】过点作于，连，根据垂径定理得，在中，，，利用含30度的直角三角形三边的关系可得到，再利用勾股定理计算出，由得到答案．
解：过点作于，连，如图
则，
在中，，，
则，
在中，，，
则，
则．
故答案为6．
【点拨】本题考查了垂径定理，含30度的直角三角形三边的关系以及勾股定理，熟悉相关性质是解题的关键．
36．(1)证明见解析；(2)证明见解析.
【分析】（1）由OD⊥AC OD为半径，根据垂径定理，即可得，又由在同圆或等圆中，同弧或等弧所对的圆周角相等，即可证得BD平分∠ABC；
（2）首先由OB=OD，易求得∠AOD的度数，又由OD⊥AC于E，可求得∠A的度数，然后由AB是⊙O的直径，根据圆周角定理，可得∠ACB=90°，继而可证得BC=OD．
解：（1）∵OD⊥AC OD为半径，∴，∴∠CBD=∠ABD，
∴BD平分∠ABC；
（2）∵OB=OD，∴∠OBD=∠0DB=30°，∴∠AOD=∠OBD+∠ODB=30°+30°=60°，
又∵OD⊥AC于E，∴∠OEA=90°，
∴∠A=180°﹣∠OEA﹣∠AOD=180°﹣90°﹣60°=30°，
又∵AB为⊙O的直径，∴∠ACB=90°，在Rt△ACB中，BC=AB，
∵OD=AB，
∴BC=OD．
37．（1）5 （2）
【分析】(1)设⊙O的半径为r，根据垂径定理求出AC的长，在Rt△OAC中利用勾股定理求出r的值；
(2)连接BE，由AE是直径，根据圆周角定理得到∠ABE=90°，利用OC是△ABE的中位线得到BE=2OC=6，然后在Rt△CBE中利用勾股定理可计算出CE．
解：(1)设⊙O半径为r，则OA＝OD＝r，OC＝r﹣2，
∵OD⊥AB，
∴∠ACO＝90°，
AC＝BC＝AB＝4，
在Rt△ACO中，由勾股定理得：r2＝42+（r﹣2）2，
r＝5，
∴OD＝r＝5；
(2)连接BE，如图：
由(1)得：AE＝2r＝10，
∵AE为⊙O的直径，
∴∠ABE＝90°，
由勾股定理得：BE＝6，
在Rt△ECB中，EC＝＝＝2．
故答案为(1)5；(2).
【点拨】本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
38．（1）证明见解析；（2）3；
【解析】
【分析】（1）先根据圆周角定理得出∠BAD=∠BCD，再由直角三角形的性质得出∠ANE=∠CNM，故可得出∠BCD=∠BAM，由全等三角形的判定定理得出△ANE≌△ADE，故可得出结论；
（2）先根据AE的长，设NE=x，则OE=x-1，NE=ED=x，r=OD=OE+ED=2x-1，连结AO，则AO=OD=2x-1，在Rt△AOE中根据勾股定理可得出x的值，进而得出结论；
解：（1）证明：∵∠BAD与∠BCD是同弧所对的圆周角，
∴∠BAD=∠BCD，
∵AE⊥CD，AM⊥BC，
∴∠AMC=∠AEN=90°，
∵∠ANE=∠CNM，
∴∠BCD=∠BAM，
∴∠BAM=BAD，
在△ANE与△ADE中，
，
∴△ANE≌△ADE，
∴AD=AN；
（2）∵AE=2，AE⊥CD，
又∵ON=1，
∴设NE=x，则OE=x-1，NE=ED=x，
r=OD=OE+ED=2x-1
连结AO，则AO=OD=2x-1，
∵△AOE是直角三角形，AE=2，OE=x-1，AO=2x-1，
∴（2）2+（x-1）2=（2x-1）2，
解得x=2，
∴r=2x-1=3.
【点拨】本题考查的是垂径定理，勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．