初中数学人教版九年级下册第二十八章 锐角三角函数28.2 解直角三角形及其应用精品课后练习题

这是一份初中数学人教版九年级下册第二十八章 锐角三角函数28.2 解直角三角形及其应用精品课后练习题，共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）
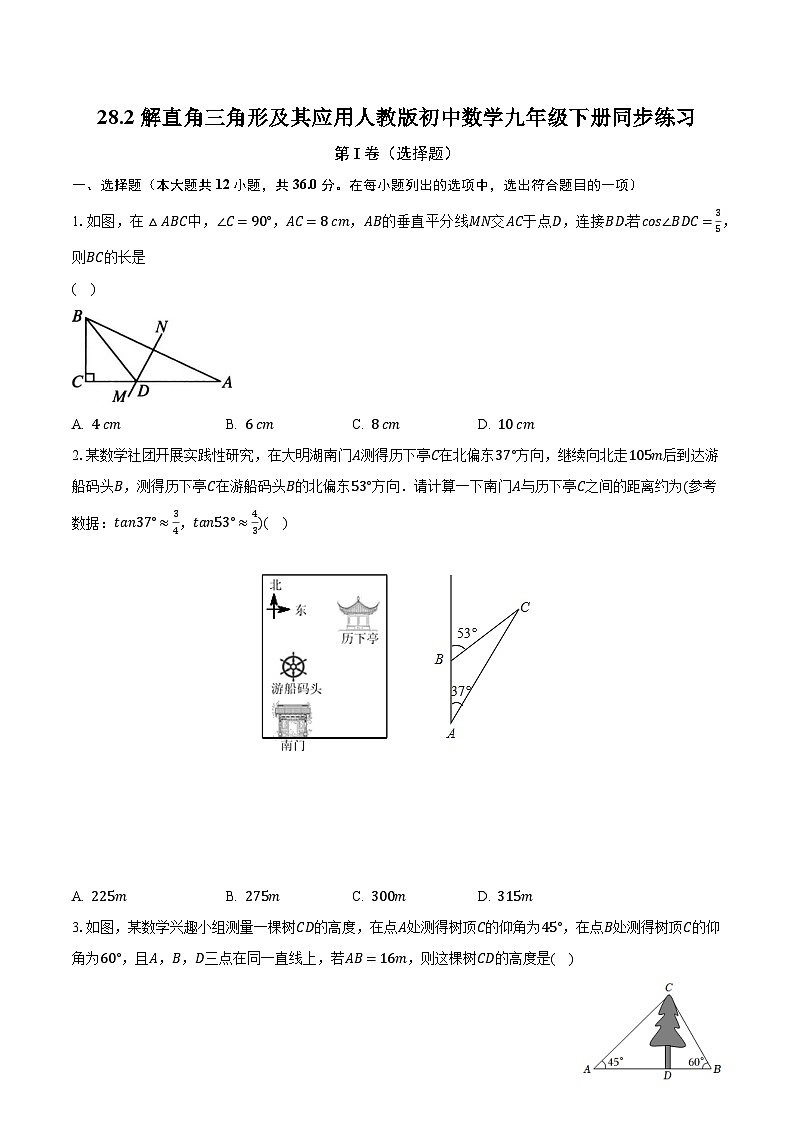
1.如图，在△ABC中，∠C=90°，AC=8 cm，AB的垂直平分线MN交AC于点D，连接BD.若cs∠BDC=35，则BC的长是
( )
A. 4 cmB. 6 cmC. 8 cmD. 10 cm
2.某数学社团开展实践性研究，在大明湖南门A测得历下亭C在北偏东37°方向，继续向北走105m后到达游船码头B，测得历下亭C在游船码头B的北偏东53°方向．请计算一下南门A与历下亭C之间的距离约为(参考数据：tan37°≈34，tan53°≈43)( )
A. 225mB. 275mC. 300mD. 315m
3.如图，某数学兴趣小组测量一棵树CD的高度，在点A处测得树顶C的仰角为45°，在点B处测得树顶C的仰角为60°，且A，B，D三点在同一直线上，若AB=16m，则这棵树CD的高度是( )
A. 8(3− 3)mB. 8(3+ 3)mC. 6(3− 3)mD. 6(3+ 3)m
4.“儿童放学归来早，忙趁东风放纸鸢”，小明周末在龙潭公园草坪上放风筝，已知风筝拉线长100米且拉线与地面夹角为65°(如图所示，假设拉线是直的，小明身高忽略不计)，则风筝离地面的高度可以表示为( )
A. 100sin65°
B. 100cs65°
C. 100tan65°
D. 100sin65∘
5.如图，在△ABC中，∠BAC=90°，AB=AC，点D为边AC的中点，DE⊥BC于点E，连接BD，则tan∠DBC的值为
( )
A. 13B. 2−1C. 2− 3D. 14
6.苏州虎丘塔是我国江南著名的园林景点.它建成于宋代(961年)，共7层，高h米.由于地基的原因，塔身自400年前就开始向西北方向倾斜.据测量，至今塔顶的中心偏离底层中心铅垂线的角度为α，被称为“东方比萨斜塔”.如今虎丘塔塔顶的中心偏离底层中心铅垂线的距离是
米( )
A. h⋅csα
B. h⋅sinα
C. h⋅tanα
D. htanα
7.如图，在天定山滑雪场滑雪，需从山脚下A处乘缆车上山顶B处，缆车索道与水平线所成的∠BAC=α，若山的高度BC=800米，则缆车索道AB 的长为
( )
A. 800sinα米B. 800csα米C. 800sinα米D. 800csα米
8.如图，在Rt△ABC中，∠C=90∘，BC= 5，点D是AC上一点，连接BD.若tanA=12，tan∠ABD=13，则CD的长为( )
A. 2 5B. 3C. 5D. 2
9. 如图，在矩形ABCD中，点E在DC上，将矩形沿AE折叠，使点D落在BC边上的点F处．若AB=3，BC=5，则tan∠DAE的值为( )
A. 12B. 920C. 25D. 13
10.如图，梯子(长度不变)跟地面所成的锐角为∠A，关于∠A的三角函数值与梯子的倾斜程度之间，叙述正确的是( )
A. sinA的值越大，梯子越陡B. csA的值越大，梯子越陡
C. tanA的值越小，梯子越陡D. 陡缓程度与∠A的函数值无关
11.如图，小刚要测量斜坡CD旁一棵树AB的高度，已知在坡脚C处测得树顶B的仰角为60∘，在坡顶D处测得树顶B的仰角为30∘，若CD=10米，DE=5米，则树AB的高是( )
A. 5 3米B. (5 3+5)米C. 15米D. 10 3米
12.如图，在正方形ABCD中，对角线AC，BD相交于点O，点E在BC边上，且CE=2BE，连接AE交BD于点G，过点B作BF⊥AE于点F，连接OF并延长，交BC于点M，过点O作OP⊥OF交DC于点N，S四边形MONC=94，现给出下列结论：①GEAG=13；②sin∠BOF=3 1010；③OF=3 55；④OG=BG；其中正确的结论有( )
A. ①②③B. ②③④C. ①②④D. ①③④
第II卷（非选择题）
二、填空题（本大题共4小题，共12.0分）
13.如图，△ABC中，∠B=90°，BC=3，AB=5，∠A=α，易知tanα=35，聪明的小强想求tan2α的值，于是他在AB上取点D，使得CD=AD，则tan2α的值为 ．
14.如图，海上有一灯塔P，位于小岛A北偏东60°方向上，一艘轮船从小岛A出发，由西向东航行24nmile到达B处，这时测得灯塔P在北偏东30°方向上，如果轮船不改变航向继续向东航行，当轮船到达灯塔P的正南方，此时轮船与灯塔P的距离是______nmile.(结果保留一位小数， 3约等于1.73)
15.如图，某校教学楼AC与实验楼BD的水平间距CD=15 3米，在实验楼顶部B点测得教学楼顶部A点的仰角是30°，底部C点的俯角是45°，则教学楼AC的高度是______米(结果保留根号)．
16.如图，在△ABC中，∠A=30°，tanB=34，AC=6 3，求AB的长为 ．
三、解答题（本大题共9小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）
17.(本小题8.0分)
如图，A，B两点被池塘隔开，在AB外选一点C，连接AC，BC.测得BC=221m，∠ACB=45°，∠ABC=58°.根据测得的数据，求AB的长(结果取整数)．
参考数据：sin58°≈0.85，cs58°≈0.53，tan58°≈1.60．
18.(本小题8.0分)
热气球的探测器显示，从热气球A处看大楼BC顶部C的仰角为30°，看大楼底部B的俯角为45°，热气球与该楼的水平距离AD为60米，求大楼BC的高度．(结果精确到1米，参考数据： 3≈1.73)
19.(本小题8.0分)
为积极参与鄂州市全国文明城市创建活动，我市某校在教学楼顶部新建了一块大型宣传牌，如下图．小明同学为测量宣传牌的高度AB，他站在距离教学楼底部E处6米远的地面C处，测得宣传牌的底部B的仰角为60°，同时测得教学楼窗户D处的仰角为30°(A、B、D、E在同一直线上).然后，小明沿坡度i=1：1.5的斜坡从C走到F处，此时DF正好与地面CE平行．
(1)求点F到直线CE的距离(结果保留根号)；
(2)若小明在F处又测得宣传牌顶部A的仰角为45°，求宣传牌的高度AB(结果精确到0.1米， 2≈1.41， 3≈1.73)．
20.(本小题8.0分)
如图，南海某海域有两艘外国渔船A、B在小岛C的正南方向同一处捕鱼．一段时间后，渔船B沿北偏东30°的方向航行至小岛C的正东方向20海里处．
(1)求渔船B航行的距离；
(2)此时，在D处巡逻的中国渔政船同时发现了这两艘渔船，其中B渔船在点D的南偏西60°方向，A渔船在点D的西南方向，我渔政船要求这两艘渔船迅速离开中国海域．请分别求出中国渔政船此时到这两艘外国渔船的距离．(注：结果保留根号)
21.(本小题8.0分)
如图所示，C城市在A城市正东方向，现计划在A、C两城市间修建一条高速公路(即线段AC)，经测量，森林保护区的中心P在A城市的北偏东60°方向上，在线段AC上距A城市120km的B处测得P在北偏东30°方向上，已知森林保护区是以点P为圆心，100km为半径的圆形区域，请问计划修建的这条高速公路是否穿越保护区，为什么？(参考数据： 3≈1.73)
22.(本小题8.0分)
如图，D是△ABC的BC边上一点，连接AD，作△ABD的外接圆，将△ADC沿直线AD折叠，点C的对应点E落在⊙O上．
(1)求证：AE=AB．
(2)若∠CAB=90°，cs∠ADB=13，BE=2，求BC的长．
23.(本小题8.0分)
如图，为了测量某条河的对岸边C，D两点间的距离．在河的岸边与CD平行的直线EF上取两点A，B，测得∠BAC=45°，∠ABC=37°，∠DBF=60°，量得AB长为70米．求C，D两点间的距离(参考数据：sin37°≈35，cs37°≈45，tan37°≈34).
24.(本小题8.0分)
如图，在△ABC中，以AB为直径的⊙O交AC于点D，点E在⊙O上，连接DE，BE，∠BED=∠CBD．
(1)求证：BC是⊙O的切线；
(2)若AD=4，sin∠BED=35，求BC的长．
25.(本小题8.0分)
如图，已知AB是⊙O的直径，BD是⊙O的弦，点P是⊙O外的一点，PC⊥AB，垂足为点C，PC与BD相交于点E，连接PD，且PD=PE，延长PD交BA的延长线于点F．
(1)求证：PD是⊙O的切线；
(2)若DF=4，PE=72，cs∠PFC=45，求BE的长．
答案和解析
1.【答案】A
【解析】由条件知BD=AD，
又cs∠BDC=35=CDBD=CDDA，AC=8 cm，
所以CD=3 cm，BD=5 cm．
所以BC=4 cm．
2.【答案】C
【解析】解：如图，作CE⊥BA于E.设EC=xm，BE=ym．
在Rt△ECB中，tan53°=ECEB，即43=xy，
在Rt△AEC中，tan37°=ECAE，即34=x105+y，
解得x=180，y=135，
∴AC= EC2+AE2= 1802+2402=300(m)，
故选：C．
如图，作CE⊥BA于E.设EC=xm，BE=ym.构建方程组求出x，y即可解决问题．
本题考查解直角三角形的应用−方向角等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，学会利用参数构建方程组解决问题，属于中考常考题型．
3.【答案】A
【解析】【分析】
设AD=x米，则BD=(16−x)米，在Rt△ADC中，利用锐角三角函数的定义求出CD的长，然后在Rt△CDB中，利用锐角三角函数列出关于x的方程，进行计算即可解答．
本题考查了解直角三角形的应用−仰角俯角问题，熟练掌握锐角三角函数的定义是解题的关键．
【解答】
解：设AD=x米，
∵AB=16米，
∴BD=AB−AD=(16−x)米，
在Rt△ADC中，∠A=45°，
∴CD=AD⋅tan45°=x(米)，
在Rt△CDB中，∠B=60°，
∴tan60°=CDBD=x16−x= 3，
∴x=24−8 3，
经检验：x=24−8 3是原方程的根，
∴CD=(24−8 3)米，
∴这棵树CD的高度是(24−8 3)米，
故选：A．
4.【答案】A
【解析】解：如图，过点A作AC⊥BC于C，
在Rt△ABC中，sinB=ACAB，
则AC=AB⋅sinB=100sin65°(米)，
故选：A．
过点A作AC⊥BC于C，根据正弦的定义解答即可．
本题考查的是解直角三角形的应用—坡度坡角问题，掌握锐角三角函数的定义是解题的关键．
5.【答案】A
【解析】【分析】
本题考查了解直角三角形的应用、等腰直角三角形的性质．通过解直角三角形，可求出相关的边长或角的度数或三角函数值.利用等腰直角三角形的判定与性质推知BC= 2AC，DE=EC= 22DC，然后通过解直角△DBE来求tan∠DBC的值．
【解答】
解：∵在△ABC中，∠BAC=90∘，AB=AC，
∴∠ABC=∠C=45∘，BC= 2AC，
又∵点D为边AC的中点，
∴AD=DC=12AC．
∵DE⊥BC于点E，
∴∠CDE=∠C=45∘，
∴tan∠DBC=DEBE= 24AC 2AC− 24AC=13．
故选A．
6.【答案】B
【解析】【分析】
本题考查的是解直角三角形的应用−坡度坡角问题，掌握锐角三角函数的定义是解题的关键．
根据正弦的定义计算，得到答案．
【解答】解：∵AC是至今塔顶的中心偏离底层中心的铅垂线，AD垂直于地基，
∴四边形CBDA是矩形，
∴∠ABC=α
在Rt△ABC中，sin∠ABC=ACAB，
则AC=AB⋅sin∠ABC=h⋅sinα(米)，
∴如今虎丘塔塔顶的中心偏离底层中心铅垂线的距离是h⋅sinα米，
故选：B．
7.【答案】C
【解析】【分析】利用直角三角形的边角关系定理列出关系式即可得出结论．
【详解】解：在Rt △ABC 中，
∵∠ACB=90∘ ， ∠BAC=α ，
∴sinα=BCAB ，
∴AB=BCsinα=800sinα 米，
故选：C．
8.【答案】C
【解析】在Rt△ABC中，∵∠C=90∘，BC= 5，tanA=BCAC=12+，∴AC=2BC=2 5.由勾股定理得，AB= AC2+BC2= (2 5)2+( 5)2=5，过点D作DE⊥AB于点E，∵tanA=12，tan∠ABD=13
∴DEAE=12，DEBE=13，∴DE=12AE=13BE，∴BE=32AE．∵AE+BE=5，∴AE+32AE=5，∴AE=2，∴DE=1.在Rt△ADE中，∵AD2=AE2+DE2，∴AD= AE2+DE2= 22+12= 5．∵AD+CD=AC=2 5，∴CD=AC−AD=2 5− 5= 5，故选C．
9.【答案】D
【解析】解：∵四边形ABCD为矩形，
∴AD=BC=5，AB=CD=3，
∵矩形ABCD沿直线AE折叠，顶点D恰好落在BC边上的F处，
∴AF=AD=5，EF=DE，
在Rt△ABF中，BF= AF2−AB2= 25−9=4，
∴CF=BC−BF=5−4=1，
设CE=x，则DE=EF=3−x
在Rt△ECF中，∵CE2+FC2=EF2，
∴x2+12=(3−x)2，解得x=43，
∴DE=EF=3−x=53，
∴tan∠DAE=DEAD=535=13，
故选：D．
先根据矩形的性质得AD=BC=5，AB=CD=3，再根据折叠的性质得AF=AD=5，EF=DE，在Rt△ABF中，利用勾股定理计算出BF=4，则CF=BC−BF=1，设CE=x，则DE=EF=3−x，然后在Rt△ECF中根据勾股定理得到x2+12=(3−x)2，解方程即可得到x，进一步得到EF的长，再根据余弦函数的定义即可求解．
本题考查了翻折变换，矩形的性质，解直角三角形，勾股定理，灵活运用这些性质进行推理是本题的关键．
10.【答案】A
【解析】解：根据锐角三角函数的变化规律，知sinA的值越大，∠A越大，梯子越陡．
故选：A．
锐角三角函数值的变化规律：正弦值和正切值都是随着角的增大而增大，余弦值和余切值都是随着角的增大而减小．
本题主要考查解直角三角形的应用，掌握锐角三角函数值的变化规律．
11.【答案】C
【解析】在Rt△DEC中，DE=5米，DC=10米，∴sin∠DCE=DEDC=12，∴∠DCE=30∘．∵∠BCA=60∘，∴∠DCB=180∘−∠DCE−∠BCA=90∘．∵DF//AE，∴∠FDC=∠DCE=30∘．∵∠BDF=30∘，∴∠BDC=∠BDF+∠CDF=60∘.在Rt△BDC中，BC=DC⋅tan60∘=10 3米.在Rt△BCA中，AB=BC⋅sin60∘=10 3× 32=15(米)，∴树AB的高是15米，故选C．
12.【答案】D
【解析】解：如图，过点O作OH/​/BC交AE于点H，过点O作OQ⊥BC交BC于点Q，过点B作BK⊥OM交OM的延长线于点K，
∵四边形ABCD是正方形，
∴OB=12BD,OC=12AC,AC=BD,∠OBM=∠OCN=45°,OB⊥OC,AD/​/BC，
∴OB=OC，∠BOC=90°，
∴∠BOM+∠MOC=90°．
∵OP⊥OF，
∴∠MON=90°，
∴∠CON+∠MOC=90°，
∴∠BOM=∠CON，
∴△BOM≌△CON(ASA)，
∴S△BOM=S△CON，
∴S四边形MONC=S△BOC=12OB⋅OC=94，
∴OB=OC=3 22，
∴BC=3 22× 2=3．
∵CE=2BE，
∴BE=13BC=1，
∴AE= AB2+BE2= 10．
∵BF⊥AE，
∴12AE⋅BF=12AB⋅ME，
∴BF=3 1010，
∴AF= AB2−BF2=9 1010，
∴HF=2 105,EF= 1010，
∴OFFM=HFEF=OHME=4，
∴ME=14OH=14×1=14，
∴BM=34,BQ=34．
∵AD/​/BC，
∴GEAG=BEAD=13，故①正确；
∵OH/​/BC，
∴OHEC=AOAC=AHAE=12,∠HOG=∠GBE，
∴OH=ME,AH=HE= 102．
∵∠HGO=∠EGB，
∴△HOG≌△EBG，
∴OG=BG，故④正确；
∵OQ2+MQ2=OM2，
∴OM= OQ2+MQ2=3 54，
∴OF=3 54×45=3 55，故③正确；
∵12OM⋅BK=12BM⋅OQ，
即12×3 54⋅BK=12×34×32，
∴BK=3 510，
∴sin∠BOF=BKOB= 1010，故②错误；
∴正确的有①③④．
故选：D．
①直接根据平行线分线段成比例即可判断正误；②过点O作OH/​/BC交AE于点H，过点O作OQ⊥BC交BC于点Q，过点B作BK⊥OM交OM的延长线于点K，首先根据四边形MONC的面积求出正方形的边长，利用勾股定理求出AE，AF，EF的长度，再利用平行线分线段成比例分别求出OM，BK的长度，然后利用sin∠BOF=BKOB即可判断；③利用平行线分线段成比例得出OFFM=4，然后利用勾股定理求出OM的长度，进而OF的长度可求；④直接利用平行线的性质证明△HOG≌△EBG，即可得出结论．
本题主要考查了四边形综合，熟练掌握正方形的性质，全等三角形的判定及性质，平行线分线段成比例和锐角三角函数是解题的关键
13.【答案】158
【解析】【分析】
根据等边对等角可得∠A=∠ACD，再利用三角形的外角性质可知∠CDB=2α，然后在Rt△CDB中利用勾股定理先求出BD，最后利用正切定义即可解答．
本题考查了解直角三角形，勾股定理，三角形的外角性质等知识点，根据题目的已知条件得到∠CDB=2α是解题的关键．
【解答】
解：∵CD=AD，
∴∠A=∠ACD=α，
∵∠CDB是△ACD的外角，
∴∠CDB=∠A+∠ACD=2α，
在Rt△CDB中，设BD为x，则AD=CD=AB−x=5−x，
∵BC2+BD2=CD2，
∴32+x2=5−x2，
整理，得10x=16，
∴x=1.6，
∴BD=1.6，
∴tan∠CDB=BCBD=31.6=158，
∴tan2α=158，
故答案为：158．
14.【答案】20.8
【解析】【分析】
本题考查了解直角三角形的应用−方向角问题，等腰三角形的判定与性质等知识，正确作出高线，转化为直角三角形的计算是解决本题的关键．
过P作PD⊥AB于D，易证△ABP是等腰三角形，得到BP=AB=24nmile.然后在直角△PBD中，利用三角函数的定义求得PD的长即可．
【解答】
解：过P作PD⊥AB于D．
∵∠PAB=30°，∠PBD=60°，
∴∠PAB=∠APB，
∴BP=AB=24nmile．
在直角△PBD中，PD=BP⋅sin∠PBD=24× 32=12 3≈20.8(nmile)．
即此时轮船与灯塔P的距离约为20.8nmile．
故答案为20.8．
15.【答案】(15+15 3)
【解析】【分析】
本题考查了解直角三角形应用．
首先通过分析图形构造直角三角形：△BEC与△ABE，进而可解即可求出答案．
【解答】
解：过点B作BE⊥AC于点E，
在Rt△BEC中，∠CBE=45°，BE=CD=15 3，
可得CE=BE×tan45°=15 3米．
在Rt△ABE中，∠ABE=30°，BE=15 3，
可得AE=BE×tan30°=15米．
故教学楼AC的高度是AC=(15 3+15)米．
16.【答案】9+4 3
【解析】【分析】
作CD⊥AB于D，根据含30度的直角三角形三边的关系得到CD=3 3，AD=9，再在Rt△BCD中根据正切的定义可计算出BD，然后把AD与BD相加即可．
本题考查了解直角三角形、含30°角的直角三角形的性质、三角函数定义等知识；熟练掌握含30°角的直角三角形的性质和三角函数定义是解题的关键．
【解答】
解：作CD⊥AB于D，如图，
在Rt△ACD中，∠A=30°，AC=6 3，
∴CD=12AC=3 3，AD= 3CD=9，
在Rt△BCD中，tanB=CDBD=34，
∴BD=43CD=4 3，
∴AB=AD+BD=9+4 3；
故答案为：9+4 3．
17.【答案】解：如图，过点A作AD⊥BC，垂足为D，
∵∠ACB=45°，
∴AD=CD，
设AB=x，
在Rt△ADB中，AD=AB⋅sin58°≈0.85x，BD=AB⋅cs58°≈0.53x，
又∵BC=221，即CD+BD=221，
∴0.85x+0.53x=221，
解得，x≈160，
答：AB的长约为160m．
【解析】通过作高，构造直角三角形，利用直角三角形的边角关系，列方程求解即可．
本题考查直角三角形的边角关系，掌握直角三角形的边角关系，即锐角三角函数，是正确解答的前提，通过作辅助线构造直角三角形是常用的方法．
18.【答案】解：由题意可得，AD=60米，∠ADC=∠ADB=90°，
∴在Rt△ADC中，∠CAD=30°，AD=60米，
∴tan∠CAD=CDAD=CD60= 33，
∴CD=20 3(米)，
在Rt△ADB中，∠DAB=45°，AD=60米，
∴tan∠DAB=BDAD=1，
∴BD=60(米)，
∴BC=BD+CD=(60+20 3)≈95(米)，
即这栋楼的高度BC是95米．
【解析】在直角三角形ADB中和直角三角形ACD中，根据锐角三角函数中的正切可以分别求得BD和CD的长，从而可以求得BC的长，本题得以解决．
本题考查解直角三角形的应用−仰角俯角问题、锐角三角函数，解答此类问题的关键是明确题意，利用锐角三角函数解答．
19.【答案】解：(1)过点F作FG⊥EC于G，
依题意知FG/​/DE，DF//GE，∠FGE=90° ；
∴四边形DFGE是矩形；
∴FG=DE；
在Rt△CDE中，
DE=CE⋅tan∠DCE；
=6×tan30 =2 3 (米)；
∴点F到地面的距离为2 3 米；
(2)∵斜坡CF的坡比i=1：1.5．
∴Rt△CFG中，CG=1.5FG=2 3×1.5=3 3(米)，
∴FD=EG=(3 3+6)米．
在Rt△BCE中，
BE=CE⋅tan∠BCE=6×tan60 =6 3米．
∴AB=AD+DE−BE．
=3 3+6+2 3−6 3=6− 3≈4.3 (米)．
答：宣传牌的高度约为4.3米．
【解析】(1)过点F作FG⊥EC于G，依题意知FG/​/DE，DF//GE，∠FGE=90° ；得到四边形DEFG是矩形；根据矩形的性质得到FG=DE；解直角三角形即可得到结论；
(2)解直角三角形即可得到结论．
本题考查的是解直角三角形的应用−仰角俯角问题，正确标注仰角和俯角、熟记锐角三角函数的定义是解题的关键．
20.【答案】解：(1)由题意得，∠CAB=30°，∠ACB=90°，BC=20，
∴AB=2BC=40海里，
答：渔船B航行的距离是40海里；
(2)过B作BE⊥AE于E，过D作DH⊥AE于H，延长CB交DH于G，
则四边形AEBC和四边形BEHG是矩形，
∴BE=GH=AC=20 3(海里)，AE=BC=20(海里)，
设BG=EH=x(海里)，
∴AH=x+20(海里)，
由题意得，∠BDG=60°，∠ADH=45°，
∴DG= 33x，DH=AH，
∴20 3+ 33x=x+20，
解得：x=20 3，
∴BG=20 3，AH=20+20 3(海里)，
∴BD=BG 32=40(海里)，
AD= 2AH=20 2+20 6(海里)，
答：中国渔政船此时到外国渔船B的距离是40海里，到外国渔船A的距离是(20 2+20 6)海里．
【解析】(1)由题意得到∠CAB=30°，∠ACB=90°，BC=20，根据直角三角形的性质即可得到结论；
(2)过B作BE⊥AE于E，过D作DH⊥AE于H，延长CB交DH于G，得到四边形AEBC和四边形BEHG是矩形，根据矩形的性质得到BE=GH=AC=20 3，AE=BC=20，设BG=EH=x，求得AH=x+20，解直角三角形即可得到结论．
本题主要考查了解直角三角形的应用−方向角问题，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．
21.【答案】解：结论；不会．理由如下：
作PH⊥AC于H．
由题意可知：∠EAP=60°，∠FBP=30°，
∴∠PAB=30°，∠PBH=60°，
∵∠PBH=∠PAB+∠APB，
∴∠BAP=∠BPA=30°，
∴BA=BP=120，
在Rt△PBH中，sin∠PBH=PHPB，
∴PH=PB⋅sin60°=120× 32≈103.80(km)，
∵103.80>100，
∴这条高速公路不会穿越保护区．
【解析】作PH⊥AC于H.求出PH与100比较即可解决问题．
本题考查解直角三角形、等腰三角形的判定和性质、三角形外角的性质等知识，解题的关键是灵活运用所学知识解决问题，学会添加常用辅助线，构造直角三角形解决问题．
22.【答案】解：(1)由折叠的性质可知，△ADE≌△ADC，
∴∠AED=∠ACD，AE=AC，
∵∠ABD=∠AED，
∴∠ABD=∠ACD，
∴AB=AC，
∴AE=AB；
(2)如图，过A作AH⊥BE于点H，
∵AB=AE，BE=2，
∴BH=EH=1，
∵∠ABE=∠AEB=∠ADB，cs∠ADB=13，
∴cs∠ABE=cs∠ADB=13，
∴BHAB=13．
∴AC=AB=3，
∵∠BAC=90°，AC=AB，
∴BC=3 2．
【解析】(1)由折叠得出∠AED=∠ACD、AE=AC，结合∠ABD=∠AED知∠ABD=∠ACD，从而得出AB=AC，据此得证；
(2)作AH⊥BE，由AB=AE且BE=2知BH=EH=1，根据∠ABE=∠AEB=∠ADB知cs∠ABE=cs∠ADB=BHAB=13，据此得AC=AB=3，利用勾股定理可得答案．
本题主要考查三角形的外接圆，解题的关键是掌握折叠的性质、圆周角定理、等腰三角形的性质及三角函数的应用等知识点．
23.【答案】解：过点C、D分别作CM⊥EF，DN⊥EF，垂足为M、N，
在Rt△AMC中，∵∠BAC=45°，
∴AM=MC，
在Rt△BMC中，∵∠ABC=37°，tan∠ABC=CMBM，
∴BM=CMtan37∘=43CM，
∵AB=70=AM+BM=CM+43CM，
∴CM=30=DN，
在Rt△BDN中，∵∠DBN=60°，
∴BN=DNtan60∘=30 3=10 3，
∴CD=MN=MB+BN=43×30+10 3=40+10 3，
答：C，D两点间的距离为(40+10 3)米，
【解析】本题考查直角三角形的边角关系的应用，掌握直角三角形的边角关系以及几个直角三角形之间的关系是正确解答的关键．
通过作辅助线，在三个直角三角形中，根据边角关系，分别求出CM、BM、DN、BN，进而求出答案．
24.【答案】(1)证明：∵AB是⊙O的直径，
∴∠ADB=90°。
∵∠BED=∠CBD，∠BED=∠BAD，
∴∠CBD=∠BAD，
∴∠ABC=∠CBD+∠ABD=∠BAD+∠ABD=90°．
∵OB是⊙O的半径，且BC⊥OB，
∴BC是⊙O的切线．
(2)解：∵∠ADB=90°，∠BAD=∠BED=∠CBD，
∴BDAB=sin∠BAD=sin∠BED=35．
设BD=3m，则AB=5m，
∴AD= AB2−BD2= (5m)2−(3m)2=4m，
∴4m=4，解得m=1，
∴BD=3．
∵∠BDC=180°−∠ADB=90°，
∴CDBC=sin∠CBD=sin∠BED=35，
∴CD=35BC．
∵BD2+CD2=BC2，
∴32+(35BC)2=BC2，
∴BC=154或BC=−154(不符合题意，舍去)，
∴BC的长是154．
【解析】(1)由AB是⊙O的直径，得∠ADB=90°，由∠BED=∠CBD=∠BAD，得∠ABC=∠CBD+∠ABD=∠BAD+∠ABD=90°，即可证明BC是⊙O的切线．
(2)由∠ADB=90°，∠BAD=∠BED=∠CBD，得BDAB=sin∠BAD=sin∠BED=35，设BD=3m，则AB=5m，AD= AB2−BD2=4m，所以4m=4，则m=1，所以BD=3，由CDBC=sin∠CBD=sin∠BED=35，得CD=35BC，则32+(35BC)2=BC2，即可求得BC=154．
此题重点考查切线的判定、圆周角定理、勾股定理、锐角三角函数与解直角三角形等知识，证明∠BAD=∠BED=∠CBD是解题的关键．
25.【答案】(1)证明：连接OD，
∵OD=OB，
∴∠ODB=∠OBD，
∵PD=PE，
∴∠PDE=∠PED，
∵PC⊥AB，
∴∠BCE=90°，
∴∠OBC+∠BEC=90°，
∵∠PED=∠BEC，
∴∠BEC=∠PDE，
∴∠PDE+∠BCO=90°，
∴∠PDO=90°，
∵OD是⊙O的半径，
∴PD是⊙O的切线；
(2)解：∵PD=PE=72，
∴PF=PD+FD=152，
在Rt△PFC中，∵cs∠PFC=CFFP=45，
∴CF=6，
在Rt△ODF中，∵cs∠PFC=DFOF=4OF=45，
∴OF=5，
∴OC=CF−OF=1，OD= OF2−FD2= 52−42=3，
∴OB=OD=3，
∴BC=OB−OC=2，
∵PC= PF2−CF2=92，
∴CE=PC−PE=1，
∴BE= BC2+CE2= 22+12= 5．
【解析】(1)连接OD，根据等腰三角形的性质得到∠ODB=∠OBD，∠PDE=∠PED，根据切线的判定定理即可得到PD是⊙O的切线；
(2)连接AD，解直角三角形即可得到结论．
本题考查了切线的判定和性质，勾股定理，三角函数的定义，等腰三角形的性质，正确地作出辅助线是解题的关键．