数学选择性必修 第二册第二章 导数及其应用4 导数的四则运算法则4.2 导数的乘法与除法法则教学演示课件ppt

这是一份数学选择性必修 第二册第二章 导数及其应用4 导数的四则运算法则4.2 导数的乘法与除法法则教学演示课件ppt，共34页。PPT课件主要包含了素养目标•定方向，必备知识•探新知，关键能力•攻重难，题型探究，易错警示，课堂检测•固双基等内容，欢迎下载使用。
§4　导数的四则运算法则4．1　导数的加法与减法法则4．2　导数的乘法与除法法则
 1．掌握导数的四则运算法则．2．能利用导数的四则运算法则求导函数． 通过利用导数的四则运算法则求导函数，培养数学运算素养.
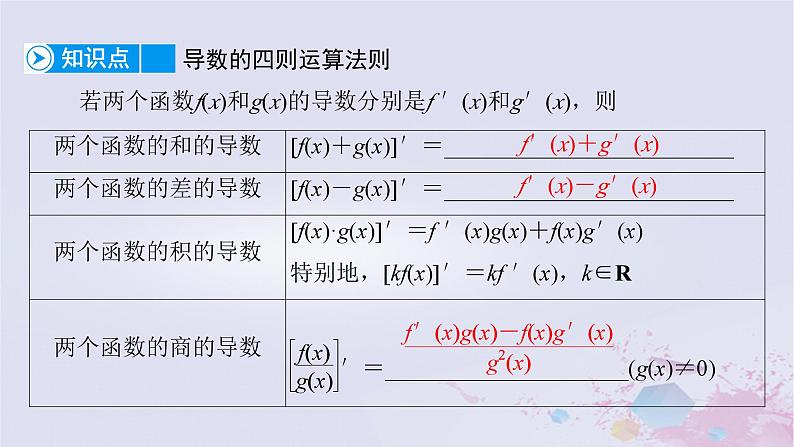
若两个函数f(x)和g(x)的导数分别是f ′(x)和g′(x)，则
f′(x)＋g′(x)
f′(x)－g′(x)
[提醒]　注意区分两个函数积与商的求导公式中符号的异同，积的导数公式中是“＋”，而商的导数公式中分子上是“－”．
想一想：若两个函数的导数存在，那么这两个函数的和、差、积、商(商分母不为零)的导数是否存在？提示：两个函数的导数存在，则它们的和、差、积、商(商分母不为零)必存在；若两个函数的导数不存在，则它们的和、差、积、商不一定不存在．
练一练：1．已知函数f(x)＝ln x－f′(1)x2＋2x－1，则f(1)的值为( 　　)A．－1B．0 C．1D．2
2．函数f(x)＝(x＋1)2(x－1)在x＝1处的导数等于( 　　)A．1B．2 C．3D．4[解析]　f(x)＝(x＋1)2(x－1)＝x3＋x2－x－1，f′(x)＝3x2＋2x－1，f′(1)＝3＋2－1＝4.
3．若函数f(x)＝(2πx)2，则f′(－1)＝( 　　)A．8π2B．－8π2C．4π2D．－4π2[解析]　f(x)＝(2πx)2＝4π2x2，所以f′(x)＝8π2x，f′(－1)＝8π2×(－1)＝－8π2.
求下列函数的导数．
[分析]　若所给函数解析式较为复杂，可先对函数解析式进行适当的变化与化简，再用相关公式和法则求导．[解析]　(1)方法一：可以先展开后再求导：y＝(2x2－1)(3x＋1)＝6x3＋2x2－3x－1，∴y′＝(6x3＋2x2－3x－1)′＝18x2＋4x－3.方法二：可以利用乘法的求导法则进行求导：y′＝(2x2－1)′(3x＋1)＋(2x2－1)(3x＋1)′＝4x(3x＋1)＋3(2x2－1)＝12x2＋4x＋6x2－3＝18x2＋4x－3.
[规律方法]　应用导数的四则运算法则的思路方法及注意事项(1)熟记导数的四则运算法则，尤其是积、商的求导法则．(2)应用和、差、积、商的求导法则求导数时，在可能的情况下，应尽量少用甚至不用积或商的求导法则，应在求导之前，先利用代数、三角恒等变形等知识对函数进行化简，然后再求导，这样可以减少运算量，提高运算速度，避免出错．(3)对于三个以上函数的积、商的导数，依次转化为“两个”函数的积、商的导数计算．
求下列函数的导数：(1)y＝(x2＋1)(x－1)；(2)y＝3x＋lg x；
已知曲线f(x)＝x3＋ax＋b在点P(2，－6)处的切线方程是13x－y－32＝0.(1)求a，b的值；
[分析]　(1)由f(x)在点P处的切线方程可知f′(2)，及f(2)＝－6，得到a，b的方程组，解方程组可求出a，b；(2)由曲线y＝f(x)的切线与l垂直，可得切线斜率k＝f′(x0)，从而解出x0，求得切点坐标和k.
[解析]　(1)∵f(x)＝x3＋ax＋b的导数f′(x)＝3x2＋a，由题意可得f′(2)＝12＋a＝13, f(2)＝8＋2a＋b＝－6，解得a＝1，b＝－16.
[规律方法]　1.导数的应用中，求导数是一个基本解题环节，应仔细分析函数解析式的结构特征，根据导数公式及运算法则求导数，不具备导数运算法则的结构形式时，先恒等变形，然后分析题目特点，探寻条件与结论的联系，选择解题途径．2．求参数的问题一般依据条件建立参数的方程求解．
已知a∈R，设函数f(x)＝ax－ln x的图象在点(1，f(1))处的切线为l，则l在y轴上的截距为_____.
不能正确应用导数的运算法则而致误
[解析]　函数的导数为f ′(x)＝1＋ex，故选D.
3．若函数f(x)＝excs x，则此函数图象在点(1，f(1))处的切线的倾斜角为( 　　)A．0B．锐角C．直角D．钝角