初中北师大版1 平行四边形的性质课前预习ppt课件

这是一份初中北师大版1 平行四边形的性质课前预习ppt课件，共17页。PPT课件主要包含了欣赏图片引入新课，动手操作形成定义，实践探索发现性质，推理论证验证性质，应用巩固运用性质，评价反思归纳小结，作业布置等内容，欢迎下载使用。

“哪里有数学，哪里就有美！” ——古希腊数学家普洛克拉斯
数学中的几何图形，在我们的生活中无处不在，它给这个五彩缤纷的世界增添了许多美感。
图中有你认识的几何图形吗？
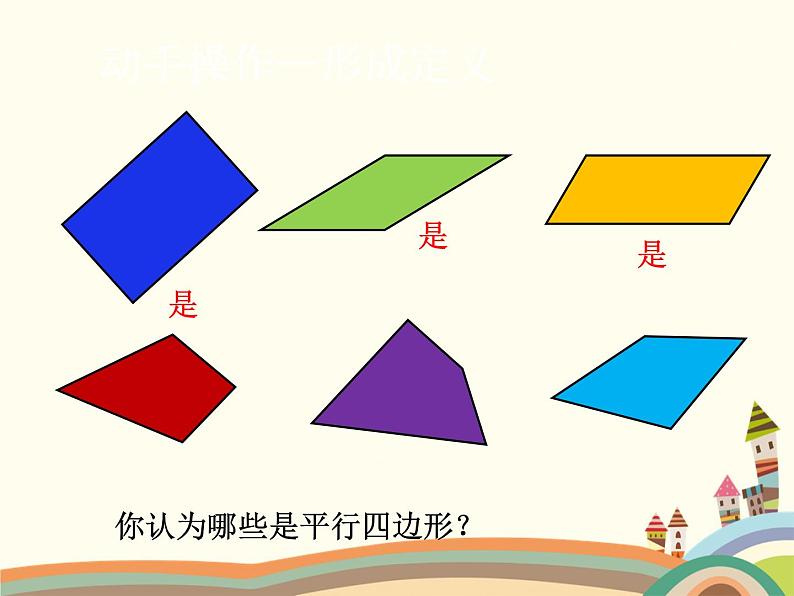
你认为哪些是平行四边形？
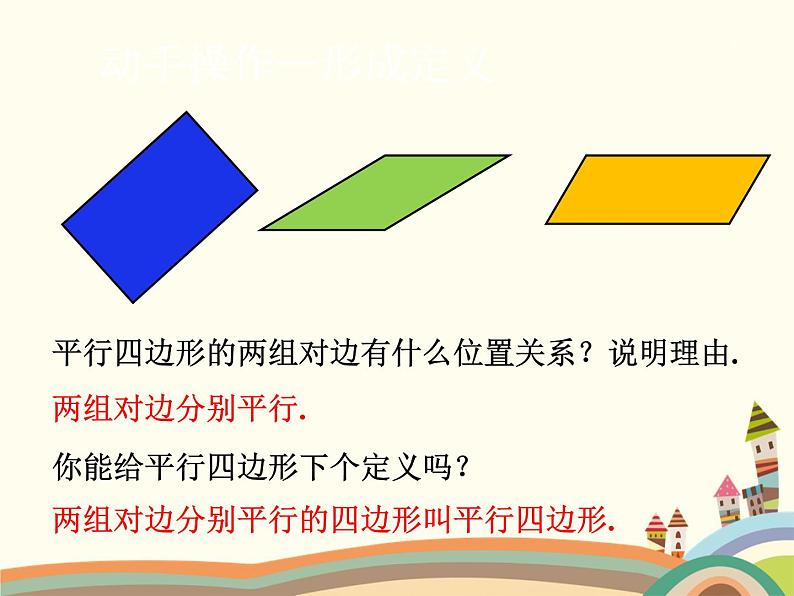
平行四边形的两组对边有什么位置关系？说明理由.两组对边分别平行.你能给平行四边形下个定义吗？两组对边分别平行的四边形叫平行四边形.
平行四边形定义中的两个条件：①四边形，②两边分别平行，即AD∥BC， AB∥DC.平行四边形的表示： .平行四边形不相邻的两个顶点连成线段叫做它的对角线.找一找：平行四边形的对边、邻边、对角、邻角.
生活中常见到平行四边形的实例有哪些呢？你能举例说明吗？
想一想：（1）由平行四边形的定义你能直接知道它的对边具有什么位置关系吗？说说你的理由.两组对边分别平行.（2）用两个全等的三角形纸片可以拼出几种形状不同的平行四边形？从拼图可以得到什么启示？平行四边形可以由两个全等的三角形拼成，因此在解决平行四边形的问题时，通常可以连接对角线转化为两个全等的三角形进行解题.
小组活动：可采取度量、平移、旋转、折叠、拼图等方法探究平行四边形的对称性以及边、角的数量关系.平行四边形是中心对称图形，不是轴对称图形，并且平行四边形两条对角线的交点是它的对称中心；平行四边形的邻角互补.定理：平行四边形的对边相等.定理：平行四边形的对角相等.
你能推导这两个定理吗？提示：证明命题的一般步骤：（1）结合命题，画出图形；（2）根据图形结合命题的条件和结论写出已知和求证；（3）找出由“已知”推导出“求证”的途径；（4）写出证明过程.
定理：平行四边形的对边相等.定理：平行四边形的对角相等.
已知：四边形ABCD是平行四边形.求证： AB=CD， BC=DA， ∠B= ∠D，∠BAD= ∠DCB.
证明：连接AC，∵四边形ABCD是平行四边形，∴ AB∥CD， BC∥DA.∴ ∠1= ∠2， ∠3= ∠4.∵ AC = CA，∴ △ABC≌ △CDA（ASA）.∴ AB=CD， BC=DA.∴ ∠B= ∠D，∠BAD= ∠DCB.
小试牛刀：（1）在平行四边形ABCD 中，已知∠A= 130°，则∠B=_____ ，∠C=_____， ∠D= _____；（2）平行四边形ABCD 中，∠A比∠B 大20°，则∠C=_____；（3）在平行四边形ABCD 中，AD= 30， CD= 25，则AB=_____， BC=_____ .
例1.已知：如图，在平行四边形ABCD 中，E，F是对角线AC上的两点，且AE=CF.求证： BE=DF.
证明：∵四边形ABCD 是平行四边形，∴ AB=CD，AB∥CD，∴ ∠BAE= ∠DCF. 又∵ AE=CF，∴△BAE≌△DCF.∴ BE=DF.
联系拓广：如图，在平行四边形ABCD 中， ∠ABC平分线交CD于点F，∠ADC的平分线交AB于点E.求证： BE=DF.
证明：∵四边形ABCD 是平行四边形，∴ AD=BC，∠A= ∠C，∴ ∠ADC= ∠ABC. 又∵ ∠ABC平分线交CD于点F，∠ADC平分线交AB于点E，∴ ∠ADE= ∠CBF.∴△ADE≌△CBF.∴ AE=CF.又∵ AB=CD，∴ AB-AE=CD-CF. ∴ BE=DF.
通过这节课的学习，你有哪些收获？还有什么疑惑？
教材习题6.1第1，2 题.