初中数学北师大版九年级下册1 二次函数背景图课件ppt

这是一份初中数学北师大版九年级下册1 二次函数背景图课件ppt，共20页。PPT课件主要包含了导入新知，议一议寻找规律，有00，对称轴y轴，做一做巩固新知，1列表，2描点，3连线，y-x2，相同都是抛物线等内容，欢迎下载使用。

二次函数的定义是什么？有什么注意事项？
二次函数：一般地，若两个变量x，y之间的对应关系可以表示成y=ax2+bx+c(a，b，c是常数，a≠0)的形式，则称y是x的二次函数.注意：含x项的最高次数是2，且二次项系数不能为0.
画二次函数y=x2的图象
画二次函数y=x2的图象.
（1）观察y=x2的表达式，选择适当的x值，并计算相应的y值，完成下表：
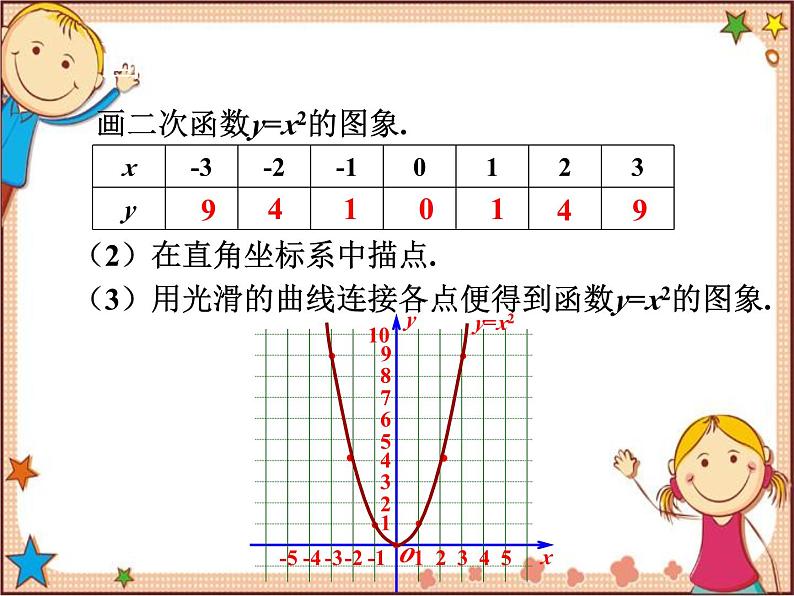
画二次函数y=x2的图象.
（2）在直角坐标系中描点.
（3）用光滑的曲线连接各点便得到函数y=x2的图象.
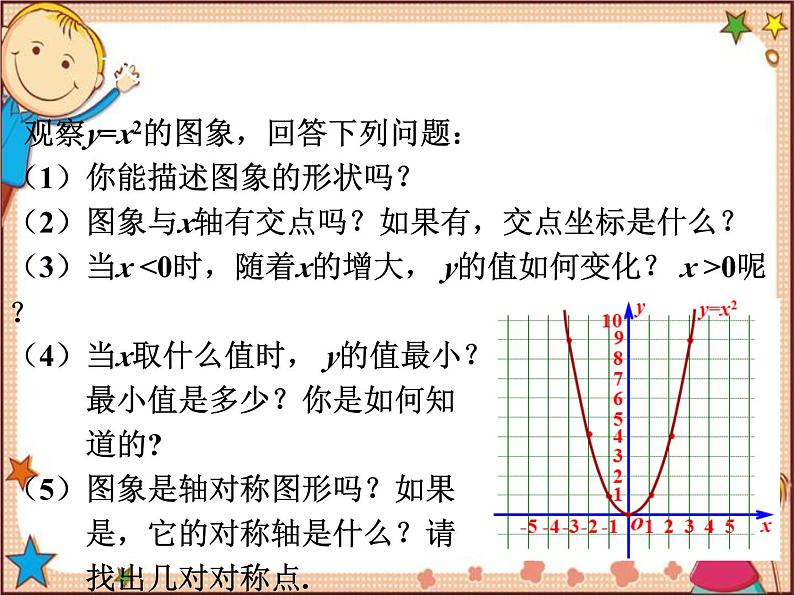
观察y=x2的图象，回答下列问题：（1）你能描述图象的形状吗？（2）图象与x轴有交点吗？如果有，交点坐标是什么？（3）当x <0时，随着x的增大， y的值如何变化？ x >0呢？（4）当x取什么值时， y的值最小？ 最小值是多少？你是如何知 道的?（5）图象是轴对称图形吗？如果 是，它的对称轴是什么？请 找出几对对称点.
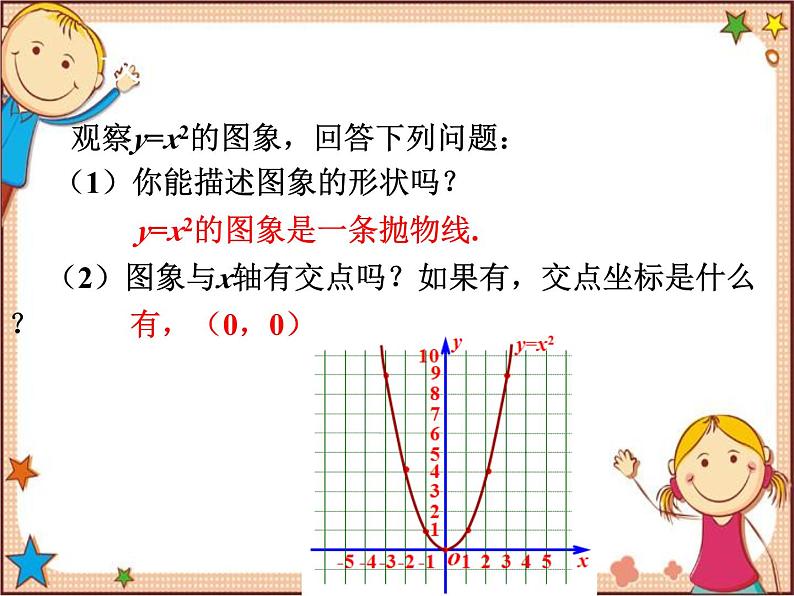
观察y=x2的图象，回答下列问题： （1）你能描述图象的形状吗？
y=x2的图象是一条抛物线.
（2）图象与x轴有交点吗？如果有，交点坐标是什么？
观察y=x2的图象，回答下列问题： （3）当x <0时，随着x的增大， y的值如何变化？ x >0呢？ （4）当x取什么值时， y的值最小？最小值是多少？你是如何知道的?
当x =0时，y的值最小，最小值是0.
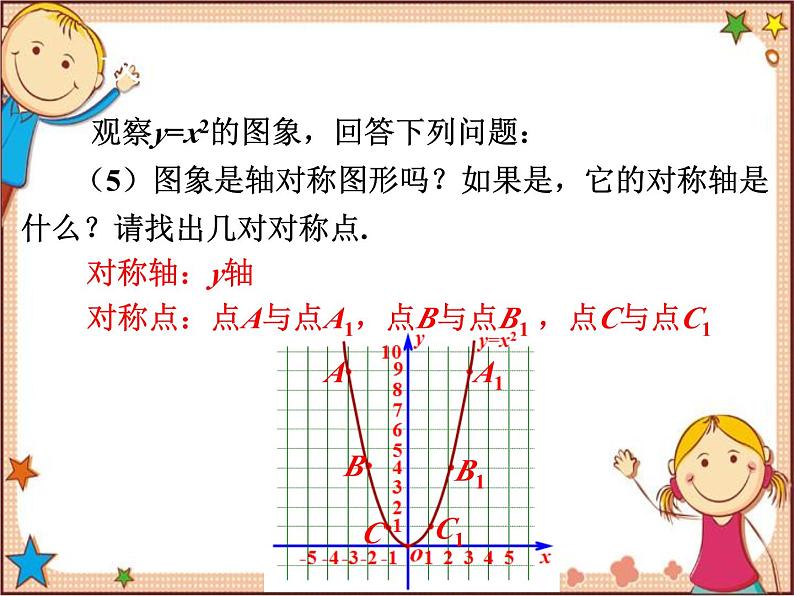
观察y=x2的图象，回答下列问题： （5）图象是轴对称图形吗？如果是，它的对称轴是什么？请找出几对对称点.
对称点：点A与点A1，点B与点B1 ，点C与点C1
二次函数y=x2的图象是一条抛物线，它的开口向上，且关于y轴对称.对称轴与抛物线的交点是抛物线的顶点，它是图象的最低点.
猜想一下，二次函数y=-x2的图象是什么形状？
思考：（1）二次函数y=-x2与y=x2的图象形状是否相同？
思考：（2）寻找二次函数y=-x2与y=x2的图象之间的联系以及区别.
思考：（3）比较二次函数y=-x2与y=x2的图象随着x值的变化， y值的变化规律.
在对称轴左侧递减在对称轴右侧递增
在对称轴左侧递增在对称轴右侧递减
根据以上问题的探讨，你能说说二次函数中二次项系数的符号的实际含义吗？
（1）令点P的坐标是（x，y）,求△POA的面积S与y之间的函数关系式； （2） S是y的什么函数？ S是x的什么函数？
1.如图，点P是抛物线y=x2上第一象限内的一个点，点A的坐标是（3，0）.
S是y的一次函数，S是x的二次函数
2.正方形的边长为x，面积为y，试画出y随x的变化而变化的图象，它的图象是一条抛物线吗？为什么？
y=x2，是二次函数，它的图象是一条抛物线的一部分，因为正方形的边长不可能为负值.
归纳本节所学的内容，谈谈本节的收获，填写成长记录卡.
教材习题2.2第2题.