北师大版数学九年级下册 3.4 圆周角和圆心角的关系第1课时 圆周角定理 课件

这是一份北师大版数学九年级下册 3.4 圆周角和圆心角的关系第1课时 圆周角定理 课件，共19页。

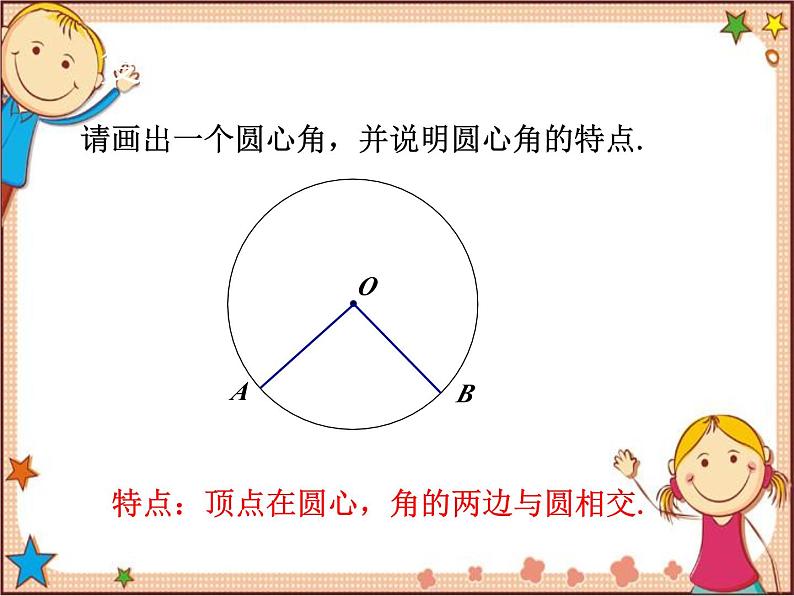
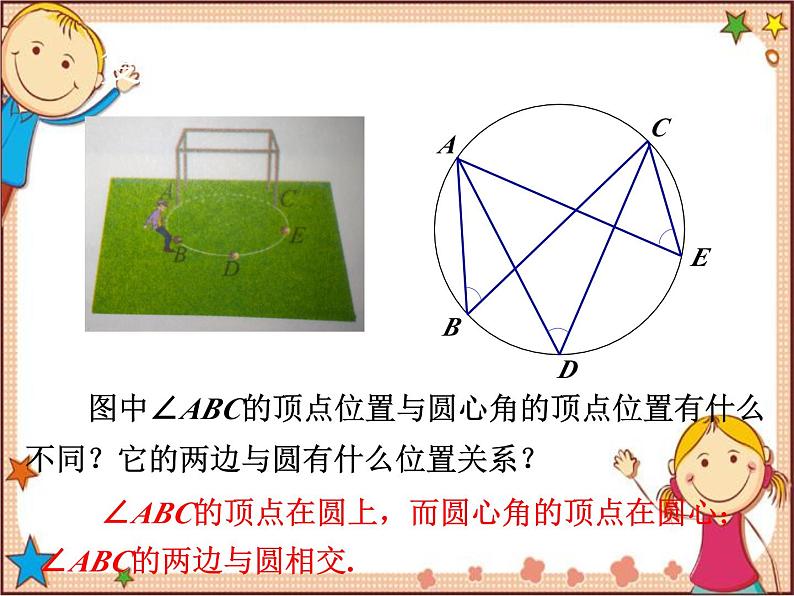
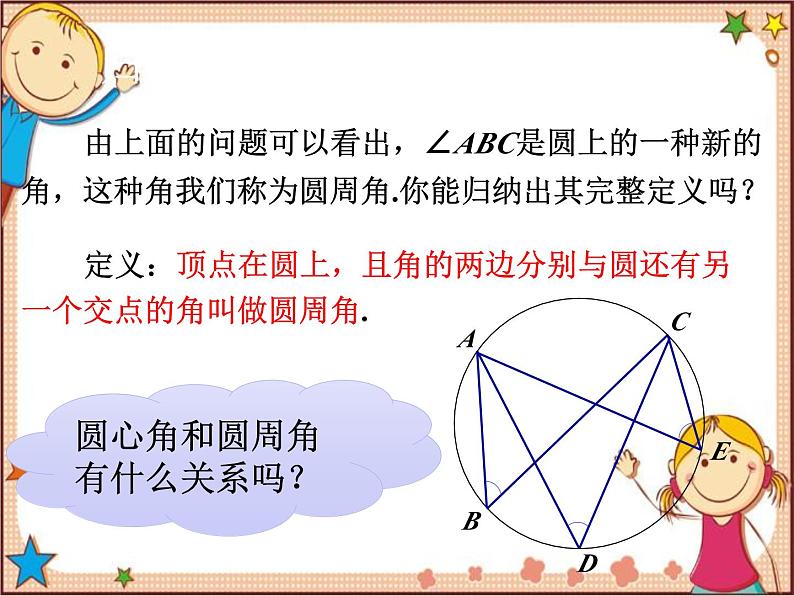
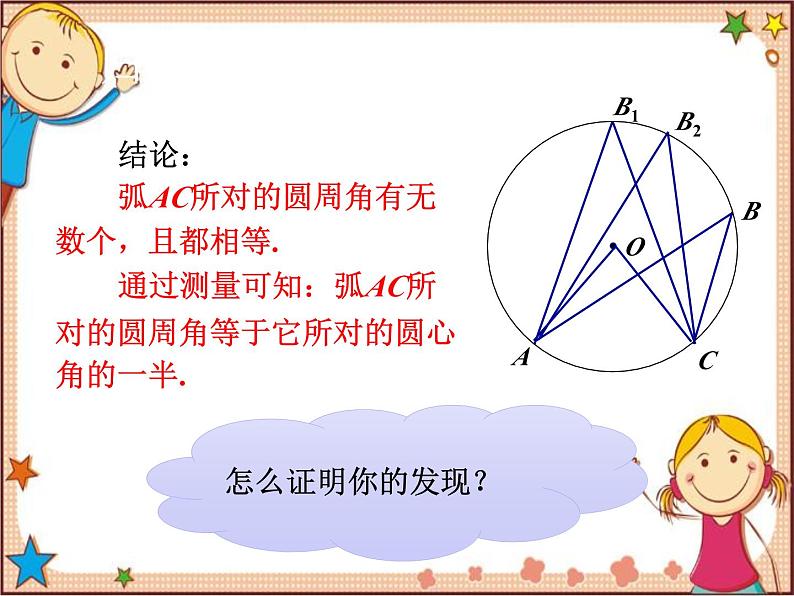
第3章 圆 3.4 圆周角和圆心角的关系第1课时 圆周角定理复习导课请画出一个圆心角，并说明圆心角的特点.特点：顶点在圆心，角的两边与圆相交.复习导课图中∠ABC的顶点位置与圆心角的顶点位置有什么不同？它的两边与圆有什么位置关系？∠ABC的顶点在圆上，而圆心角的顶点在圆心；∠ABC的两边与圆相交.归纳新知由上面的问题可以看出，∠ABC是圆上的一种新的角，这种角我们称为圆周角.你能归纳出其完整定义吗？定义：顶点在圆上，且角的两边分别与圆还有另一个交点的角叫做圆周角.圆心角和圆周角有什么关系吗？归纳新知（1）在上图中，当球员在B，D，E处射门时，他所处的位置对球门AC分别形成三个角∠ABC，∠ADC，∠AEC.这三个角的大小有什么关系？归纳新知（2）在同圆或者等圆中，相等的弧所对的圆心角相等.那么，在同圆或等圆中，相等的弧所对的圆周角有什么关系？相等归纳新知请同学们画出⊙O中弧AC所对的圆周角或圆心角.思考：弧AC所对的圆周角有多少个？它们的大小有什么关系？弧AC所对的圆周角与圆心角有什么关系？B1BB2归纳新知结论：弧AC所对的圆周角有无数个，且都相等.通过测量可知：弧AC所对的圆周角等于它所对的圆心角的一半.怎么证明你的发现？B1BB2归纳新知结论：弧AC所对的圆周角等于它所对的圆心角的一半.已知：圆O中，弧AC所对的圆周角是∠ABC，圆心角是∠AOC.求证：归纳新知如果∠ABC的两边都不经过圆心，那么结果会怎样？你能利用特殊结果把问题解决吗？①点O在∠ABC内部时，只要作出直径BD，将这个角转化为上述情况的两个角的和即可证出.D归纳新知如果∠ABC的两边都不经过圆心，那么结果会怎样？你能利用特殊结果把问题解决吗？②点O在∠ABC外部时，只要作出直径BD，将这个角转化为上述情况的两个角的差即可证出.D归纳新知由刚才的讨论研究，你能总结出什么规律？圆周角定理：圆周角的度数等于它所对弧上的圆心角度数的一半.归纳新知三个张角∠ABC，∠ADC和∠AEC有什么关系呢？它们会相等吗？∠ABC，∠ADC和∠AEC是同弧（弧AC）所对的圆周角，根据我们所学的圆周角定理可知，它们都等于圆心角∠AOC的一半，所以这几个圆周角相等.即∠ ABC=∠ADC=∠AEC.归纳新知总结规律：圆周角定理推论1：同弧或等弧所对的圆周角相等.应用练习，巩固提高随堂练习1.如图，在⊙O中，∠O=50°，求∠A的度数.∠A=25°应用练习，巩固提高随堂练习2.如图，哪个角与∠BAC相等？你还能找到哪些相等的角？∠ BDC = ∠BACD∠ ADB= ∠ACB∠ DAC = ∠DBC∠ ABD = ∠ACD1.本节课学的知识：（1）圆周角的定义.（2）圆周角定理.（3）圆周角定理推论1.2.本节课的数学方法：“由特殊到一般”的数学思想方法.课堂小结教材第80~81页习题3.4第1，2题.布置作业谢谢大家！再见！