初中数学北师大版九年级下册第三章 圆1 圆课前预习课件ppt

这是一份初中数学北师大版九年级下册第三章 圆1 圆课前预习课件ppt，共21页。PPT课件主要包含了创设情境引入新课，讲授新课，切线的判定定理，例题讲解，课堂练习，锐角三角形，直角三角形，钝角三角形，课堂小结，布置作业等内容，欢迎下载使用。

观察下面的图片，在下雨天当车从我们身边飞驰而过时，我们会看到车轮后留下 一条水流痕迹，砂轮打磨零件会飞出火星，如果我们把车轮和砂轮看作一个圆，留下的水流痕迹和飞出的火星看作一条直线，大家探索一下这一生活现象中的直线和圆又有怎样的位置关系呢？
上节课我们掌握了切线的性质，那么如何判断一条直线是圆的切线呢？
切线的性质定理的逆命题是什么？它的逆命题正确吗？也和其他的定理一样可以作为切线的判定定理吗？
切线的性质定理：圆的切线垂直于过切点的半径.
逆命题：过半径外端且垂直于这条半径的直线是圆的切线.
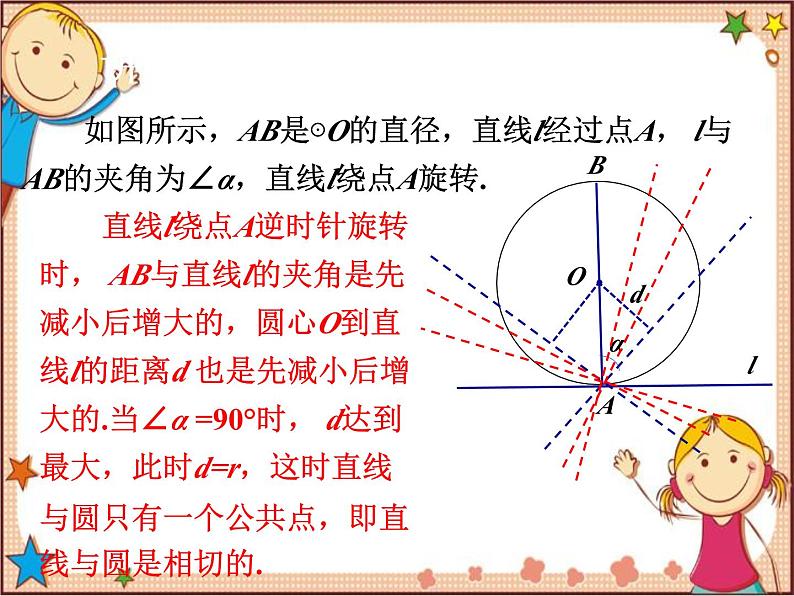
如图所示，AB是⊙O的直径，直线l经过点A， l与AB的夹角为∠α，直线l绕点A旋转.
（1）随着∠α的变化，点O到l的距离d如何变化？直线l与⊙O的位置关系如何变化？
（2）当∠α等于多少度时，点O到l的距离d等于半径r？此时，直线l与⊙O有怎样的位置关系？为什么？
直线l绕点A逆时针旋转时， AB与直线l的夹角是先减小后增大的，圆心O到直线l的距离d 也是先减小后增大的.当∠α =90°时， d达到最大，此时d=r，这时直线与圆只有一个公共点，即直线与圆是相切的.
过半径外端且垂直于这条半径的直线是圆的切线.
用数学语言表示：∵ AB是⊙O的直径，直线CD经过点A，且CD⊥AB，∴ CD是⊙O的切线.
判定圆的切线要满足两个条件：一是直线经过半径的外端；二是垂直于这条半径.
作法：（1）连接OA.（2）过点A作OA的垂线l.直线l即为所求的切线.
做一做 已知⊙O上一点A，过点A画⊙O的切线.
想一想：作图的依据是什么？
依据：经过直径的一端，并且垂直于这条直径的直线是圆的切线.
拓展延伸 已知⊙O外一点P，过点P作出⊙O的切线.
已知⊙O外一点P，过点P作出⊙O的切线，可以作出两条，作图时可以以OP为直径作圆，与⊙O相交于A，B两点，然后作射线PA， PB即得⊙O的两条切线.
想一想：这个作图的依据是什么？
依据：直径所对的圆周角是90°.
已知：△ABC.求作：⊙I，使它与△ABC的三边都相切.
思考：1.这样的圆你能作出几个？2.交点I到三角形三边的距离有什么关系？
作法：1.作∠ABC， ∠ACB的平分线BE和CF，交点为I.2.过I作BC的垂线，垂足为D.3.以I为圆心，以ID的长为半径作⊙I.⊙I就是所求的圆.
因为BE和CF只有一个交点I，并且I到三边的距离相等，所以和三角形三边都相切的圆可以作出一个，并且只能作一个，这个圆叫做三角形的内切圆，内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心.
类比联想：我们知道三角形的内心是三角形三条角平分线的交点，那么内心的位置一定在三角形的内部吗？还是和外心一样有三个不同的位置？
无论锐角、直角、钝角三角形，它们的内心都在三角形的内部.
随堂练习1.以边长为3，4，5的三角形的三个顶点为圆心，分别作圆与对边相切，则这三个圆的半径分别是多少？
随堂练习2.如图，已知锐角三角形、直角三角形、钝角三角形，分别作出它们的内切圆，三角形的内心是否都在三角形内部？
1.本节知识主要有：①切线的判定定理.②三角形的内切圆定义.③三角形的内心.2.本节应用的主要数学方法：“特殊到一般”的归纳思想.
教材第93页习题3.8第1，2题.