初中数学北师大版七年级下册1 两条直线的位置关系课前预习ppt课件

这是一份初中数学北师大版七年级下册1 两条直线的位置关系课前预习ppt课件，共26页。PPT课件主要包含了观察思考探究新知，两条直线相交，一般的相交，垂直是相交的特殊情况，垂直的表示，1图形，垂直的书写形式，书写形式，练习1，①有一个角为90°等内容，欢迎下载使用。

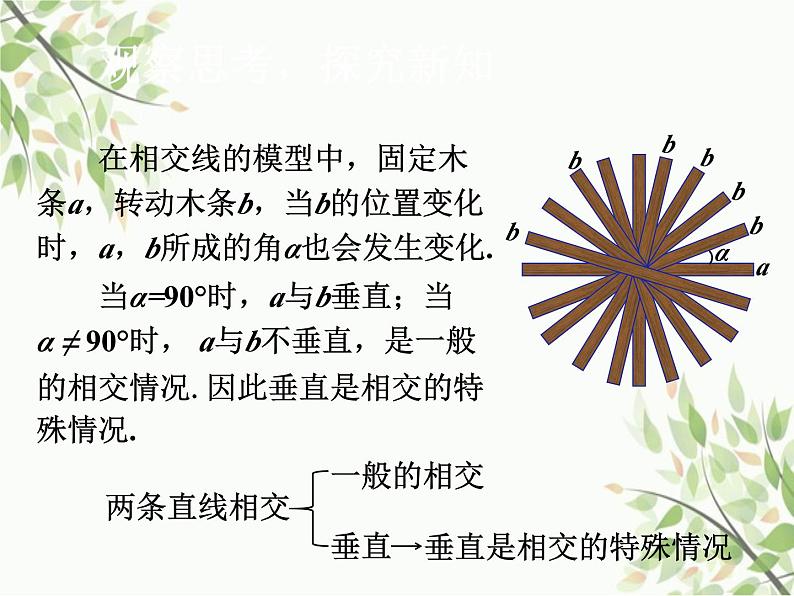
在相交线的模型中，固定木条a，转动木条b，当b的位置变化时，a，b所成的角α也会发生变化.
当α=90°时，a与b垂直；当α ≠ 90°时， a与b不垂直，是一般的相交情况.因此垂直是相交的特殊情况.
当两条直线相交所成的四个角中，有一个角是直角时，这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，它们的交点叫做垂足.
如图，直线a，b互相垂直，O叫做垂足.直线a叫做直线b的垂线，直线b也叫做直线a的垂线.
从垂直的定义可知，判断两条直线互相垂直的关键是找到两条直线相交所成的四个交角中的一个角是直角.
日常生活中，两条直线互相垂直的情形很常见，如下图中的一些互相垂直的线条.
这里还有一些其他的互相垂直的例子.
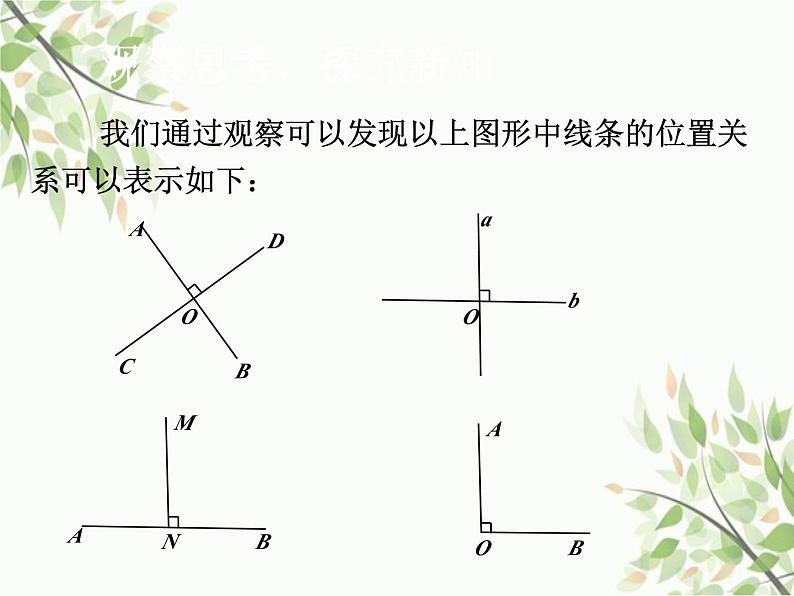
我们通过观察可以发现以上图形中线条的位置关系可以表示如下：
（2）文字：直线a，b互相垂直，垂足为O.
（3）符号：a⊥b或b⊥a，若要强调垂足，则记为： a⊥b ，垂足为O.
如图,当直线AB与CD相交于O点， ∠AOD=90°时，AB⊥CD，垂足为O.
判定：因为∠AOD=90°（已知），所以AB⊥CD（垂直的定义）.
反之，若直线AB与CD垂直，垂足为O，那么∠AOD=90°.
性质：因为AB⊥CD （已知），所以∠AOD=90° （垂直的定义）.
两条相交直线所成的四个角中，下列条件中能断定两条直线垂直的是_____________.
如图，已知直线AB，CD都经过O点，OE为射线，若∠1=35°， ∠2=55°，则OE与AB的位置关系是___________.
例 如图，直线AB，CD相交于点O，OE⊥AB，∠1=55°,求∠EOD的度数.
解：因为AB⊥OE，所以∠EOB=90°.因为∠BOD=∠1=55°，所以∠EOD=∠EOB+∠BOD=90°+55°=145°.
在小学我们曾通过折纸的方法，得到了两条垂线，现在你可以用几种折法得到两条垂线呢？
如下左图，直线a上有一点A，经过点A，你能折出几条与直线a垂直的直线？
如下右图，直线a外有一点B，经过点B，你能折出几条与直线a垂直的直线？
（1）用三角尺或量角器画已知直线l的垂线，这样的垂线能画出几条？
（2）经过直线l上一点A画l的垂线，这样的垂线能画出几条？
（3）经过直线l外一点B画l的垂线，这样的垂线能画出几条？
结论： 平面内，过一点有且只有一条直线与已知直线垂直.
【注意】过一点画已知线段（或射线）的垂线，就是画这条直线段（或射线）所在直线的垂线.
过点P向线段AB所在的直线画垂线，正确的是（ ）
点O是直线AB上的一点，OC是射线，OE平分∠AOC，OF平分∠BOC，试确定OE与OF的位置关系，并说明理由.
结论： OE ⊥ OF
理由： 因为OE平分∠AOC，OF平分∠BOC，所以∠AOC=2∠1， ∠BOC= 2∠2.又∠AOC+ ∠BOC=180°，所以2∠1+ 2∠2=180°，即∠1+ ∠2=90°，所以∠EOF=90°，即OE ⊥ OF.
探究：如图，连接直线l外一点P与直线l上各点O，A，B，C，其中PO ⊥l（我们称PO为点P到直线l的垂线段）.试比较线段PO，PA，PB，PC的长短，这些线段中，哪一条最短？
结论：直线外一点与直线上各点连接的所有线段中，垂线段最短.
我们把垂线段PO的长度叫做点P到直线l的距离.
1.要掌握好垂线、垂线段、点到直线的距离这几个概念.
2.垂线的画法.
3.垂线的性质.
平面内，过一点有且只有一条直线与已知直线垂直. 直线外一点与直线上各点连接的所有线段中，垂线段最短.
（1）画一条直线l，在直线l上取一点A，在直线l外取一点B，分别经过点A，B用三角尺或量角器画直线l的垂线.
（2）分别找出下列图中互相垂直的线段.
（2）分别找出下列图中互相垂直的线段.
（3）如图，要把水渠中的水引到C点，在渠岸AB的什么地方开沟，才能使沟最短？画出图形，并说明理由.