人教版八年级下册17.1 勾股定理示范课课件ppt

这是一份人教版八年级下册17.1 勾股定理示范课课件ppt，共21页。PPT课件主要包含了情境引入，探究新知，如何证明这个命题，拓展应用，我们应先求出什么量，先求出对角线，线段BD，线段OBOD，怎么求OBOD呢，类题运用等内容，欢迎下载使用。

毕达哥拉斯是古希腊著名的数学家，相传2 500多年前，他在朋友家做客时，发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.
（1）请同学们观察一下，下图中的等腰直角三角形有什么特点？
（2）等腰直角三角形是特殊的直角三角形，一般的直角三角形是否也满足这种特点？请观察下图.
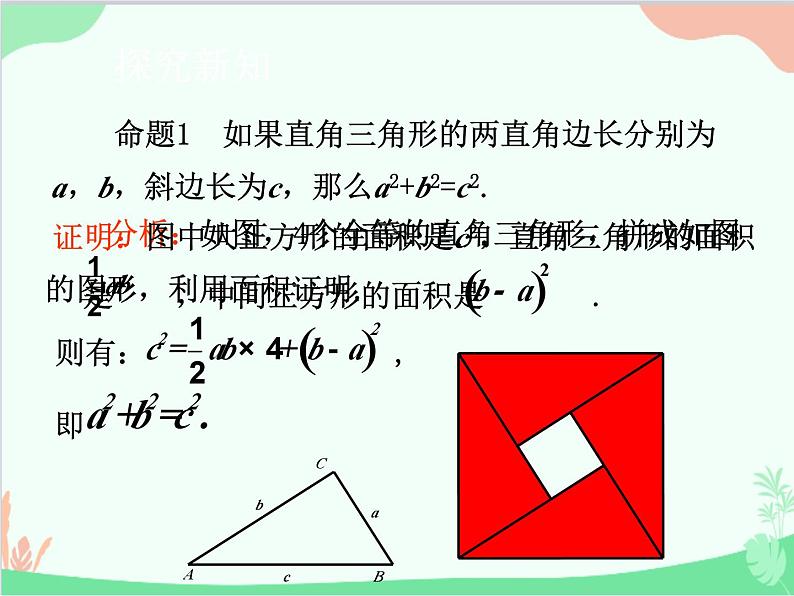
命题1 如果直角三角形的两直角边长分别为a，b，斜边长为c，那么a2+b2=c2.
分析：如图，4个全等的直角三角形，拼成如图的图形，利用面积证明.
证明：图中大正方形的面积是c2，直角三角形的面积是 ，中间正方形的面积是 .
则有： ,
命题1 如果直角三角形的两直角边长分别为a，b，斜边长为c，那么a2+b2=c2.
经过证明被确认正确的命题叫做定理.
命题1我们称之为勾股定理.
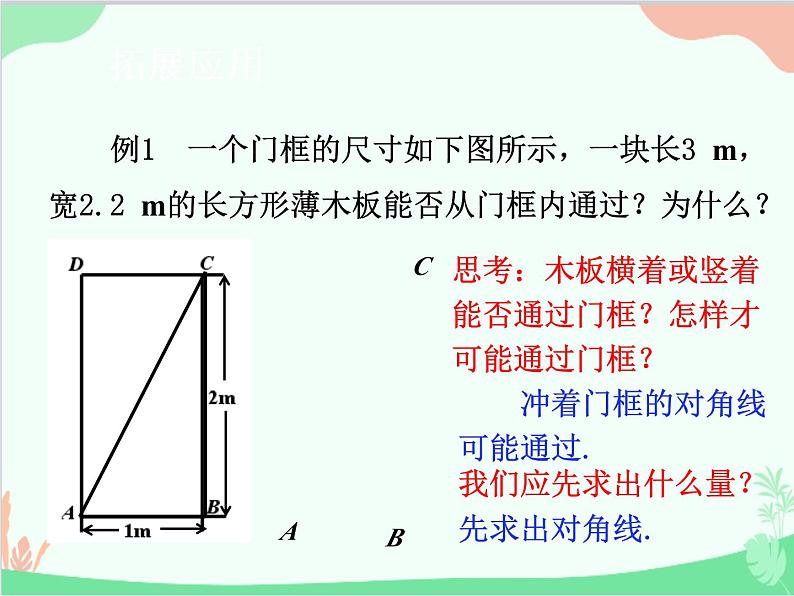
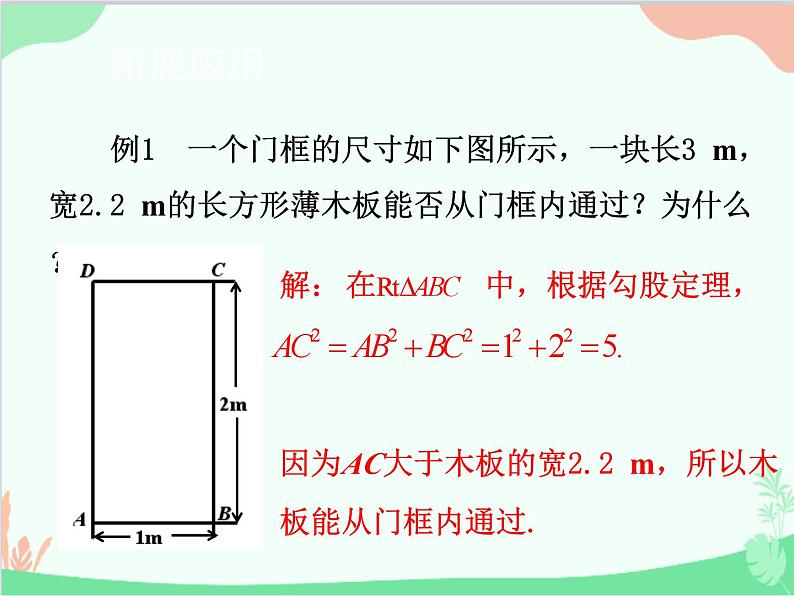
例1 一个门框的尺寸如下图所示，一块长3 m，宽2.2 m的长方形薄木板能否从门框内通过？为什么？
思考：木板横着或竖着能否通过门框？怎样才可能通过门框？
冲着门框的对角线可能通过.
在 中，根据勾股定理，
因为AC大于木板的宽2.2 m，所以木板能从门框内通过.
例2 如下图，一架2.6 m长的梯子AB，斜靠在一竖直的墙AO上，这时AO为2.4 m.如果梯子的顶端A沿墙下滑0.5 m，那么梯子底端B也外移0.5 m吗？
底端B外移的距离是指哪条线段？
要求BD，应先求出哪些线段的长？
分别在△ABO，△CDO中求.
解：在 中，OB2= , OB= .在 中,OD2= 　　　 　　　　　　　 ,OD= .所以BD= 　　　　　 .即梯子的顶端A沿墙下滑0.5 m，梯子底端B外移 .
梯子AB斜靠在墙上，梯子的底端A到墙根O的距离为2米，梯子的顶端B到地面的距离为7米.现将梯子的底端A向外移动到C，使梯子的底端C到墙根O的距离为3米，同时梯子的顶端B下降到D，那么BD： ①等于1米；②大于1米；③小于1米.其中正确的序号是______.
1.求出下列直角三角形未知边的长度.
2.在直角三角形ABC中，∠C=90°，若a=4，c=8，则b=_____.
3.如下图，将一根长24 cm的筷子，置于底面直径为5 cm，高为12 cm的圆柱形水杯中，设筷子露在杯子外面的长度是h cm，则h的取值范围是_________.
1.设直角三角形的两条直角边长分别为a和b，斜边长为c.
（1）已知a=6， c=10，求b；
（2）已知a=5， b=12，求c；
（3）已知c=25， b=15，求a.
2.如图，图中所有的三角形都是直角三角形，四边形都是正方形.已知正方形A，B，C，D的边长分别是12，16，9，12，求最大正方形E的面积.
最大正方形E的面积为625
1.如图，池塘边有两点A，B，点C是与BA方向成直角的AC方向上的一点，测得BC=60 m，AC=20 m.求A，B两点间的距离（结果取整数）.
2.如图，在平面直角坐标系中有两点A（5，0）和B（0，4）.求这两点之间的距离.
本节课学到了什么知识？还存在什么困惑？
1.勾股定理的内容.
　　2.验证勾股定理的方法.
　　 3.利用勾股定理，已知直角三角形的两边长求第三条边的长.
1.教材第28页习题17.1第1，2，3，4题.
2.课后探讨证明勾股定理的其他方法.