人教版九年级下册数学活动课文课件ppt

这是一份人教版九年级下册数学活动课文课件ppt，共18页。PPT课件主要包含了创设情境类比猜想，活动探究得出结论，它们相似，典例示范达到目标，例2解，∵ED⊥AB，∴∠EDA90°，答案14，DE∥BC，AB∥CD等内容，欢迎下载使用。

问题1：前面我们类比全等三角形的判定方法得到的两个三角形相似的判定方法有哪些？
问题2：我们现在接着验证全等三角形的AAS、ASA以及直角三角形的HL在相似三角形判定中是否也能得到推广？
有“三边法”，“两边及其夹角法”
探究1：两角相等的两个三角形是否相似？
问题1： 请大家拿出你们的含30°角的直角三角板，观察是否与老师手里拿的含30°角的直角三角板相似？
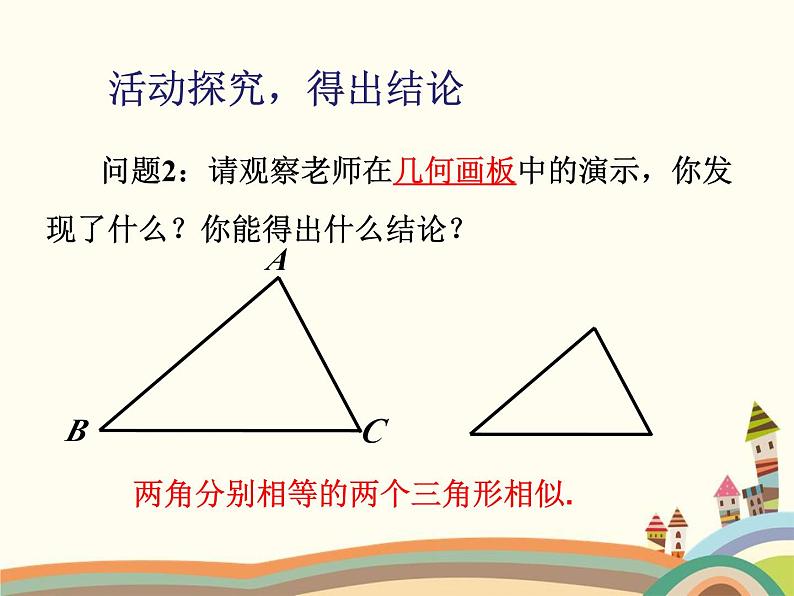
问题2：请观察老师在几何画板中的演示，你发现了什么？你能得出什么结论？
两角分别相等的两个三角形相似.
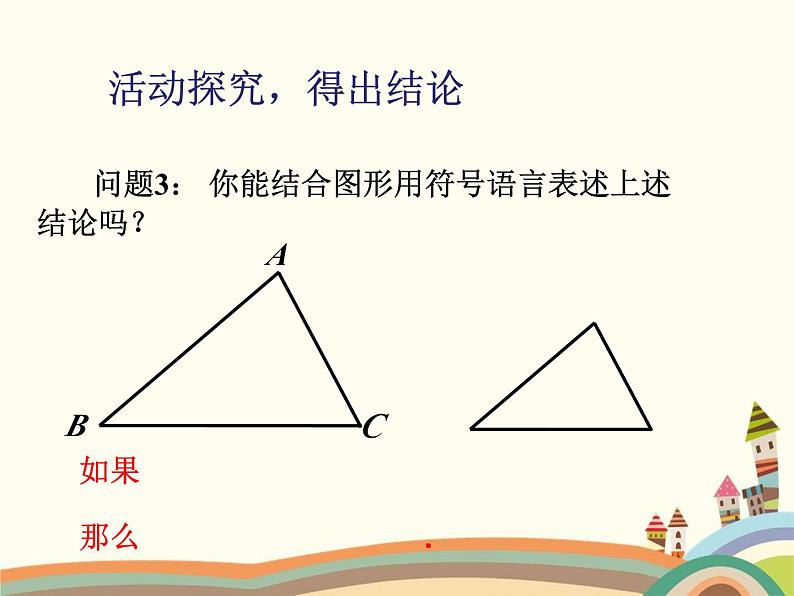
问题3： 你能结合图形用符号语言表述上述结论吗？
那么 .
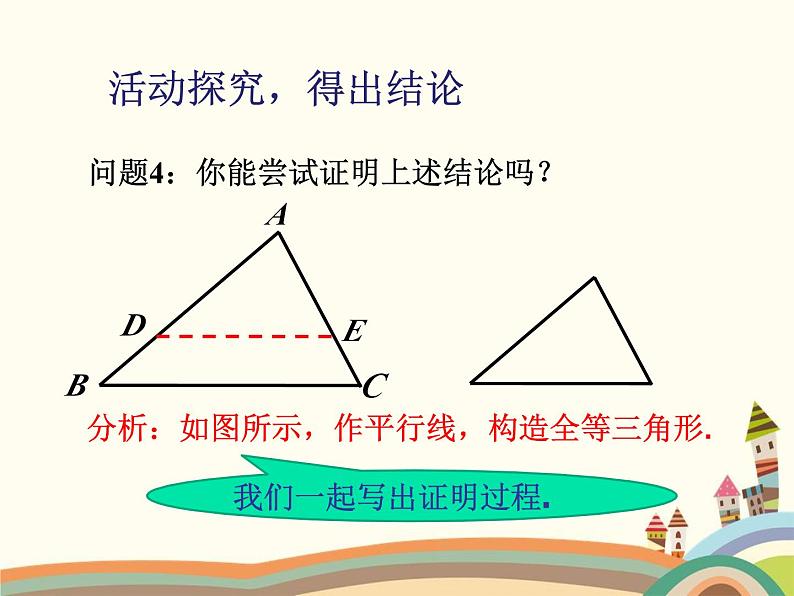
分析：如图所示，作平行线，构造全等三角形.
我们一起写出证明过程.
问题4：你能尝试证明上述结论吗？
问题5：一角对应相等的两个三角形是否相似？
(1) 请大家动手画一画验证；
(2) 请观察老师在几何画板中的演示，你发现了什么？你能得出什么结论？
一角对应相等的两个三角形不一定相似.
没有“一角对应相等的两个三角形相似”这一判定方法.
探究2：如果是两个直角三角形，判定相似的方法是否会更简洁？
问题1：你能想到哪些判定两个直角三角形相似的方法呢？
所有判定一般三角形相似的方法，都可以用来判定直角三角形相似.
由于直角三角形是特殊的三角形，所以有其特有的更简洁的判定相似的方法.
问题2：如果是一条直角边和斜边对应成比例，那么两个直角三角形相似吗？
问题3：你能归纳出判定两个直角三角形相似的条件吗？
一个锐角相等，或者两边对应成比例.
例1. 判断下列说法是否正确，并说明理由.
例2. 如图，Rt△ABC中，∠C=90°，AB=10，AC=8. E是AC上一点，AE=5，ED⊥AB，垂足为D.求AD的长.
又∵∠C=90°, ∠A=∠A,
∴△AED∽△ABC.
变式练习：若CD是Rt△ABC斜边上的高. (1)已知AD = 9，CD = 6，求BD的长；(2)已知AB = 25，BC = 15，求BD的长.
追问1：目前我们见到过哪些常见的相似基本图形？
追问2:下列图形相似吗？若不相似，那么满足什么条件才相似？
（1）∠AED=∠B，或者 等.
（2） ∠A=∠C，或者∠B=∠D，或者 等.
（1） 判定三角形相似的方法有哪些？判定直角三角形相似的方法有哪些？它们是怎么探究出来的？主要运用了什么思想？
（3）本节课你还有什么收获与困惑？
（2）利用相似主要能解决一些什么样的问题？
教材第36 页练习第1，2，3题；教材第42~43页习题27.2 第2（2），6，7，9题.