五年(19-23)中考数学真题与模拟卷分项汇编专题14 多边形与四边形（2份打包，原卷版+含解析）

这是一份五年(19-23)中考数学真题与模拟卷分项汇编专题14 多边形与四边形（2份打包，原卷版+含解析），文件包含五年19-23中考数学真题与模拟卷分项汇编专题14多边形与四边形原卷版doc、五年19-23中考数学真题与模拟卷分项汇编专题14多边形与四边形含解析doc等2份试卷配套教学资源，其中试卷共100页， 欢迎下载使用。
考点1 多边形与平行四边形
一、单选题
1．（2023年山西省中考数学真题）蜂巢结构精巧，其巢房横截面的形状均为正六边形．如图是部分巢房的横截面图，图中7个全等的正六边形不重叠且无缝隙，将其放在平面直角坐标系中，点 SKIPIF 1 < 0 均为正六边形的顶点．若点 SKIPIF 1 < 0 的坐标分别为 SKIPIF 1 < 0 ，则点 SKIPIF 1 < 0 的坐标为（ ）

A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
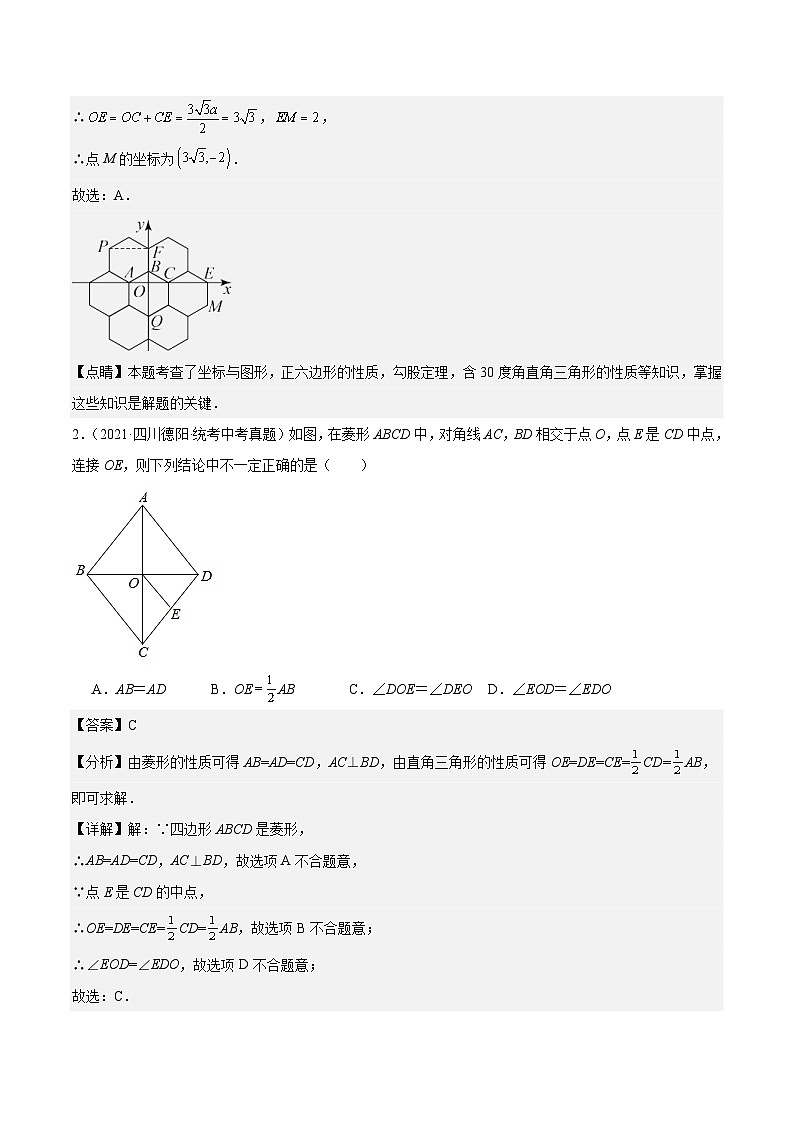
2．（2021·四川德阳·统考中考真题）如图，在菱形ABCD中，对角线AC，BD相交于点O，点E是CD中点，连接OE，则下列结论中不一定正确的是（ ）
A．AB＝ADB．OE SKIPIF 1 < 0 ABC．∠DOE＝∠DEOD．∠EOD＝∠EDO
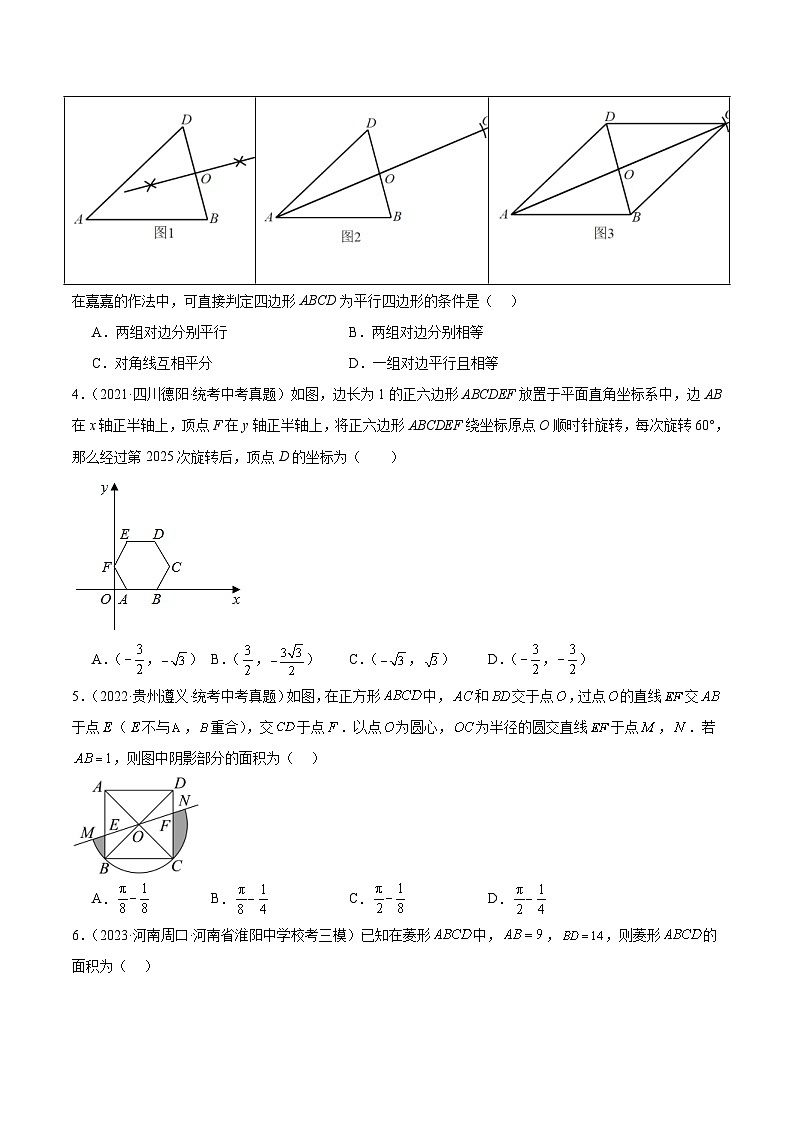
3．（2023年河北省中考数学真题）综合实践课上，嘉嘉画出 SKIPIF 1 < 0 ，利用尺规作图找一点C，使得四边形 SKIPIF 1 < 0 为平行四边形．图1~图3是其作图过程．
在嘉嘉的作法中，可直接判定四边形ABCD为平行四边形的条件是（ ）
A．两组对边分别平行B．两组对边分别相等
C．对角线互相平分D．一组对边平行且相等
4．（2021·四川德阳·统考中考真题）如图，边长为1的正六边形ABCDEF放置于平面直角坐标系中，边AB在x轴正半轴上，顶点F在y轴正半轴上，将正六边形ABCDEF绕坐标原点O顺时针旋转，每次旋转60°，那么经过第2025次旋转后，顶点D的坐标为（ ）
A．（ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ）B．（ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ）C．（ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ）D．（ SKIPIF 1 < 0 ， SKIPIF 1 < 0 ）
5．（2022·贵州遵义·统考中考真题）如图，在正方形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 和 SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 ，过点 SKIPIF 1 < 0 的直线 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 （ SKIPIF 1 < 0 不与 SKIPIF 1 < 0 ， SKIPIF 1 < 0 重合），交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ．以点 SKIPIF 1 < 0 为圆心， SKIPIF 1 < 0 为半径的圆交直线 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．若 SKIPIF 1 < 0 ，则图中阴影部分的面积为（ ）
A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
6．（2023·河南周口·河南省淮阳中学校考三模）已知在菱形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则菱形 SKIPIF 1 < 0 的面积为（ ）

A． SKIPIF 1 < 0 B．126C．63D． SKIPIF 1 < 0
7．（2020·四川巴中·统考中考真题）如图，在矩形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，对角线 SKIPIF 1 < 0 ， SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 为 SKIPIF 1 < 0 上一动点， SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，分别以 SKIPIF 1 < 0 ， SKIPIF 1 < 0 为边向外作正方形 SKIPIF 1 < 0 和 SKIPIF 1 < 0 ，面积分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．则下列结论：① SKIPIF 1 < 0 ；②点 SKIPIF 1 < 0 在运动过程中， SKIPIF 1 < 0 的值始终保持不变，为 SKIPIF 1 < 0 ；③ SKIPIF 1 < 0 的最小值为6；④当 SKIPIF 1 < 0 时，则 SKIPIF 1 < 0 ．其中正确的结论有（ ）
A．1个B．2个C．3个D．4个
二、填空题
8．（2022·江苏泰州·统考中考真题）正八边形一个外角的大小为 度．
9．（2021·江苏镇江·统考中考真题）如图，花瓣图案中的正六边形ABCDEF的每个内角的度数是 ．
10．（2023年黑龙江省齐齐哈尔市中考数学真题）如图，在四边形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ．请添加一个条件： ，使四边形 SKIPIF 1 < 0 成为菱形．

11．（2023年吉林省长春市中考数学真题）如图，将正五边形纸片 SKIPIF 1 < 0 折叠，使点 SKIPIF 1 < 0 与点 SKIPIF 1 < 0 重合，折痕为 SKIPIF 1 < 0 ，展开后，再将纸片折叠，使边 SKIPIF 1 < 0 落在线段 SKIPIF 1 < 0 上，点 SKIPIF 1 < 0 的对应点为点 SKIPIF 1 < 0 ，折痕为 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 的大小为 度．

12．（2023年内蒙古包头市中考数学真题）如图，正方形 SKIPIF 1 < 0 的边长为2，对角线 SKIPIF 1 < 0 相交于点 SKIPIF 1 < 0 ，以点 SKIPIF 1 < 0 为圆心，对角线 SKIPIF 1 < 0 的长为半径画弧，交 SKIPIF 1 < 0 的延长线于点 SKIPIF 1 < 0 ，则图中阴影部分的面积为 ．

13．（2020·四川阿坝·中考真题）如图，有一张长方形片ABCD， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．点E为CD上一点，将纸片沿AE折叠，BC的对应边 SKIPIF 1 < 0 恰好经过点D，则线段DE的长为 cm．

14．（2020·广西贺州·统考中考真题）如图，四边形ABCD是菱形，对角线AC，BD相交于点O， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点P是AC上一动点，点E是AB的中点，则 SKIPIF 1 < 0 的最小值为 ．
15．（2022·山东临沂·统考中考真题）如图，在正六边形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 是对角线 SKIPIF 1 < 0 上的两点，添加下列条件中的一个：① SKIPIF 1 < 0 ；② SKIPIF 1 < 0 ；③ SKIPIF 1 < 0 ；④ SKIPIF 1 < 0 ．能使四边形 SKIPIF 1 < 0 是平行四边形的是 （填上所有符合要求的条件的序号）．
16．（2023年内蒙古包头市中考数学真题）如图， SKIPIF 1 < 0 是正五边形 SKIPIF 1 < 0 的对角线， SKIPIF 1 < 0 与 SKIPIF 1 < 0 相交于点 SKIPIF 1 < 0 ．下列结论：
① SKIPIF 1 < 0 平分 SKIPIF 1 < 0 ； ② SKIPIF 1 < 0 ； ③四边形 SKIPIF 1 < 0 是菱形； ④ SKIPIF 1 < 0
其中正确的结论是 ．（填写所有正确结论的序号）

17．（2023年河北省中考数学真题）将三个相同的六角形螺母并排摆放在桌面上，其俯视图如图1，正六边形边长为2且各有一个顶点在直线l上，两侧螺母不动，把中间螺母抽出并重新摆放后，其俯视图如图2，其中，中间正六边形的一边与直线l平行，有两边分别经过两侧正六边形的一个顶点．则图2中
（1） SKIPIF 1 < 0 度．
（2）中间正六边形的中心到直线l的距离为 （结果保留根号）．

18．（2023·河南周口·河南省淮阳中学校考三模）如图，在矩形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，把边 SKIPIF 1 < 0 沿对角线 SKIPIF 1 < 0 平移，点 SKIPIF 1 < 0 分别对应点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的最小值为 ．

三、解答题
19．（2019·湖南娄底·中考真题）如图，点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA(不包括端点)上运动，且满足 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
(1)求证： SKIPIF 1 < 0 ；
(2)试判断四边形EFGH的形状，并说明理由．
(3)请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系，并说明理由．
20．（2019·江苏常州·统考中考真题）【阅读】：数学中，常对同一个量（图形的面积、点的个数、三角形的内角和等）用两种不同的方法计算，从而建立相等关系，我们把这一思想称为“算两次”．“算两次”也称做富比尼原理，是一种重要的数学思想．
【理解】：（1）如图，两个边长分别为 SKIPIF 1 < 0 、 SKIPIF 1 < 0 、 SKIPIF 1 < 0 的直角三角形和一个两条直角边都是 SKIPIF 1 < 0 的直角三角形拼成一个梯形．用两种不同的方法计算梯形的面积，并写出你发现的结论；
（2）如图2， SKIPIF 1 < 0 行 SKIPIF 1 < 0 列的棋子排成一个正方形，用两种不同的方法计算棋子的个数，可得等式： SKIPIF 1 < 0 ________；
【运用】：（3） SKIPIF 1 < 0 边形有 SKIPIF 1 < 0 个顶点，在它的内部再画 SKIPIF 1 < 0 个点，以（ SKIPIF 1 < 0 ）个点为顶点，把 SKIPIF 1 < 0 边形剪成若干个三角形，设最多可以剪得 SKIPIF 1 < 0 个这样的三角形．当 SKIPIF 1 < 0 ， SKIPIF 1 < 0 时，如图，最多可以剪得 SKIPIF 1 < 0 个这样的三角形，所以 SKIPIF 1 < 0 ．
①当 SKIPIF 1 < 0 ， SKIPIF 1 < 0 时，如图， SKIPIF 1 < 0 ；当 SKIPIF 1 < 0 ， SKIPIF 1 < 0 时， SKIPIF 1 < 0 ；
②对于一般的情形，在 SKIPIF 1 < 0 边形内画 SKIPIF 1 < 0 个点，通过归纳猜想，可得 SKIPIF 1 < 0 （用含 SKIPIF 1 < 0 、 SKIPIF 1 < 0 的代数式表示）．请对同一个量用算两次的方法说明你的猜想成立．
21．（2019·广西玉林·统考中考真题）如图，在正方形ABCD中，分别过顶点B，D作 SKIPIF 1 < 0 交对角线AC所在直线于E，F点，并分别延长EB，FD到点H，G，使 SKIPIF 1 < 0 ，连接EG，FH．
（1）求证：四边形EHFG是平行四边形；
（2）已知： SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求四边形EHFG的周长．
22．（2020·广西贺州·统考中考真题）如图，已知在△ABC中AB＝AC，AD是BC边上的中线，E，G分别是AC，DC的中点，F为DE延长线上的点，∠FCA＝∠CEG．
（1）求证：AD∥CF；
（2）求证：四边形ADCF是矩形．
23．（2023年吉林省长春市中考数学真题）将两个完全相同的含有 SKIPIF 1 < 0 角的直角三角板在同一平面内按如图所示位置摆放．点A，E，B，D依次在同一直线上，连结 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ．

(1)求证：四边形 SKIPIF 1 < 0 是平行四边形；
(2)已知 SKIPIF 1 < 0 ，当四边形 SKIPIF 1 < 0 是菱形时． SKIPIF 1 < 0 的长为__________ SKIPIF 1 < 0 ．
24．（2023年山西省中考数学真题）阅读与思考：下面是一位同学的数学学习笔记，请仔细阅读并完成相应任务．
任务：
(1)填空：材料中的依据1是指：_____________．
依据2是指：_____________．
(2)请用刻度尺、三角板等工具，画一个四边形 SKIPIF 1 < 0 及它的瓦里尼翁平行四边形 SKIPIF 1 < 0 ，使得四边形 SKIPIF 1 < 0 为矩形；（要求同时画出四边形 SKIPIF 1 < 0 的对角线）
(3)在图1中，分别连接 SKIPIF 1 < 0 得到图3，请猜想瓦里尼翁平行四边形 SKIPIF 1 < 0 的周长与对角线 SKIPIF 1 < 0 长度的关系，并证明你的结论．

25．（2023年北京市中考数学真题）如图，在 SKIPIF 1 < 0 中，点E，F分别在 SKIPIF 1 < 0 ， SKIPIF 1 < 0 上， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．

(1)求证：四边形 SKIPIF 1 < 0 是矩形；
(2) SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 的长．
26．（2020·广西贵港·中考真题）已知：在矩形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 是 SKIPIF 1 < 0 边上的一个动点，将矩形 SKIPIF 1 < 0 折叠，使点 SKIPIF 1 < 0 与点 SKIPIF 1 < 0 重合，点 SKIPIF 1 < 0 落在点 SKIPIF 1 < 0 处，折痕为 SKIPIF 1 < 0 ．
（1）如图1，当点 SKIPIF 1 < 0 与点 SKIPIF 1 < 0 重合时，则线段 SKIPIF 1 < 0 _______________， SKIPIF 1 < 0 _____________；
（2）如图2，当点 SKIPIF 1 < 0 与点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 均不重合时，取 SKIPIF 1 < 0 的中点 SKIPIF 1 < 0 ，连接并延长 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的延长线交于点 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．
①求证：四边形 SKIPIF 1 < 0 是平行四边形：
②当 SKIPIF 1 < 0 时，求四边形 SKIPIF 1 < 0 的面积．
27．（2021·江苏镇江·统考中考真题）如图1，∠A＝∠B＝∠C＝∠D＝∠E＝∠F＝90°，AB，FE，DC为铅直方向的边，AF，ED，BC为水平方向的边，点E在AB，CD之间，且在AF，BC之间，我们称这样的图形为“L图形”，记作“L图形ABC﹣DEF”．若直线将L图形分成面积相等的两个图形，则称这样的直线为该L图形的面积平分线．
【活动】
小华同学给出了图1的面积平分线的一个作图方案：如图2，将这个L图形分成矩形AGEF、矩形GBCD，这两个矩形的对称中心O1，O2所在直线是该L图形的面积平分线．请用无刻度的直尺在图1中作出其他的面积平分线．（作出一种即可，不写作法，保留作图痕迹）
【思考】
如图3，直线O1O2是小华作的面积平分线，它与边BC，AF分别交于点M，N，过MN的中点O的直线分别交边BC，AF于点P，Q，直线PQ （填“是”或“不是”）L图形ABCDEF的面积平分线．
【应用】
在L图形ABCDEF形中，已知AB＝4，BC＝6．
（1）如图4，CD＝AF＝1．
①该L图形的面积平分线与两条水平的边分别相交于点P，Q，求PQ长的最大值；
②该L图形的面积平分线与边AB，CD分别相交于点G，H，当GH的长取最小值时，BG的长为 ．
（2）设 SKIPIF 1 < 0 ＝t（t＞0），在所有的与铅直方向的两条边相交的面积平分线中，如果只有与边AB，CD相交的面积平分线，直接写出t的取值范围 ．
28．（2022·内蒙古赤峰·统考中考真题）同学们还记得吗？图①、图②是人教版八年级下册教材“实验与探究”中我们研究过的两个图形．受这两个图形的启发，数学兴趣小组提出了以下三个问题，请你回答：
(1)【问题一】如图①，正方形 SKIPIF 1 < 0 的对角线相交于点 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 又是正方形 SKIPIF 1 < 0 的一个顶点， SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 与 SKIPIF 1 < 0 的数量关系为_________；
(2)【问题二】受图①启发，兴趣小组画出了图③：直线 SKIPIF 1 < 0 、 SKIPIF 1 < 0 经过正方形 SKIPIF 1 < 0 的对称中心 SKIPIF 1 < 0 ，直线 SKIPIF 1 < 0 分别与 SKIPIF 1 < 0 、 SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，直线 SKIPIF 1 < 0 分别与 SKIPIF 1 < 0 、 SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ，若正方形 SKIPIF 1 < 0 边长为8，求四边形 SKIPIF 1 < 0 的面积；
(3)【问题三】受图②启发，兴趣小组画出了图④：正方形 SKIPIF 1 < 0 的顶点 SKIPIF 1 < 0 在正方形 SKIPIF 1 < 0 的边 SKIPIF 1 < 0 上，顶点 SKIPIF 1 < 0 在 SKIPIF 1 < 0 的延长线上，且 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．在直线 SKIPIF 1 < 0 上是否存在点 SKIPIF 1 < 0 ，使 SKIPIF 1 < 0 为直角三角形？若存在，求出 SKIPIF 1 < 0 的长度；若不存在，说明理由．
29．（2023年江苏省无锡市中考数学真题）如图，四边形 SKIPIF 1 < 0 是边长为 SKIPIF 1 < 0 的菱形， SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 为 SKIPIF 1 < 0 的中点， SKIPIF 1 < 0 为线段 SKIPIF 1 < 0 上的动点，现将四边形 SKIPIF 1 < 0 沿 SKIPIF 1 < 0 翻折得到四边形 SKIPIF 1 < 0 ．

(1)当 SKIPIF 1 < 0 时，求四边形 SKIPIF 1 < 0 的面积；
(2)当点 SKIPIF 1 < 0 在线段 SKIPIF 1 < 0 上移动时，设 SKIPIF 1 < 0 ，四边形 SKIPIF 1 < 0 的面积为 SKIPIF 1 < 0 ，求 SKIPIF 1 < 0 关于 SKIPIF 1 < 0 的函数表达式．
30．（2023·浙江杭州·杭州市丰潭中学校考三模）如果一个多边形的内角和是外角和的3倍，则这个多边形的边数是（ ）
A．6B．7C．8D．9
31．（2023·浙江杭州·杭州市丰潭中学校考三模）如图，在圆内接正六边形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 分别交 SKIPIF 1 < 0 于点G，H，若该圆的半径为12，则线段 SKIPIF 1 < 0 的长为（ ）

A．6B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D．8
32.（2023·河南周口·河南省淮阳中学校考三模）已知在菱形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则菱形 SKIPIF 1 < 0 的面积为（ ）

A． SKIPIF 1 < 0 B．126C．63D． SKIPIF 1 < 0
33．（2023·新疆和田·和田市第三中学校考二模）如图，在菱形 SKIPIF 1 < 0 中，分别以 SKIPIF 1 < 0 、 SKIPIF 1 < 0 为圆心，大于 SKIPIF 1 < 0 为半径画弧，两弧分别交于点 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，若直线 SKIPIF 1 < 0 恰好过点 SKIPIF 1 < 0 与边 SKIPIF 1 < 0 交于点 SKIPIF 1 < 0 ，连接 SKIPIF 1 < 0 ，则下列结论错误的是（ ）
A． SKIPIF 1 < 0 B．若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
34．（2023·辽宁·校联考三模）如图，平行四边形ABCD的对角线AC、BD相交于点O，AE平分∠BAD，分别交BC、BD于点E、P，连接OE，∠ADC=60°，AB= SKIPIF 1 < 0 BC=1，则下列结论：
①∠CAD=30°②BD= SKIPIF 1 < 0 ③S平行四边形ABCD=AB•AC④OE= SKIPIF 1 < 0 AD⑤S△APO= SKIPIF 1 < 0 ，正确的个数是（ ）
A．2B．3C．4D．5
35．（2023·广西玉林·统考一模）如图，在由边长相同的7个正六边形组成的网格中，点A，B在格点上．再选择一个格点C，使△ABC是以AB为腰的等腰三角形，符合点C条件的格点个数是( )
A．1B．2C．3D．4
36．（2023·河南驻马店·统考三模）如图，在平面直角坐标系中，点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 为线段 SKIPIF 1 < 0 的中点， SKIPIF 1 < 0 为 SKIPIF 1 < 0 上一点，连接 SKIPIF 1 < 0 ，将 SKIPIF 1 < 0 沿 SKIPIF 1 < 0 折叠得到 SKIPIF 1 < 0 ．当 SKIPIF 1 < 0 时，点 SKIPIF 1 < 0 的坐标为（ ）

A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
37．（2023·河北石家庄·石家庄市第四十一中学校考模拟预测）如图，正方形的对角线刚好与正六边形最长的对角线重合，则 SKIPIF 1 < 0 （ ）

A．10°B．15°C．20°D．25°
38．（2023·安徽滁州·校考三模）如图，以正方形 SKIPIF 1 < 0 的对角线 SKIPIF 1 < 0 为一边作菱形 SKIPIF 1 < 0 ，点F在 SKIPIF 1 < 0 的延长线上，连接 SKIPIF 1 < 0 交 SKIPIF 1 < 0 于点G，则 SKIPIF 1 < 0 ．
39．（2023·河北石家庄·石家庄市第四十一中学校考模拟预测）图1、图2的两个正方形网格的面积分别为 SKIPIF 1 < 0 、 SKIPIF 1 < 0 ，正方形 SKIPIF 1 < 0 、 SKIPIF 1 < 0 满足 SKIPIF 1 < 0 ，下列结论正确的是（ ）

A． SKIPIF 1 < 0 B． SKIPIF 1 < 0
C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
40．（2023·河南洛阳·统考三模）如图，已知四边形 SKIPIF 1 < 0 是平行四边形，下列三个结论：①当 SKIPIF 1 < 0 时，它是菱形，②当 SKIPIF 1 < 0 时，它是矩形，③当 SKIPIF 1 < 0 时，它是正方形．其中结论正确的有（ ）
A．0个B．1个C．2个D．3个
41．（2023·重庆沙坪坝·重庆南开中学校考二模）已知一个正多边形的一个外角为 SKIPIF 1 < 0 ，则这个正多边形的边数是 ．
42．（2023·云南丽江·统考二模）一个正多边形的每个外角为60°，那么这个正多边形的内角和是 ．
43．（2023·辽宁本溪·统考二模）如图，一正六边形 SKIPIF 1 < 0 的对角线 SKIPIF 1 < 0 的长为 SKIPIF 1 < 0 ，则正六边形 SKIPIF 1 < 0 的边长为 ．

44．（2023·山东济南·统考三模）将正六边形与正方形按如图所示摆放，公共顶点为 SKIPIF 1 < 0 ，且正六边形的边 SKIPIF 1 < 0 与正方形的边 SKIPIF 1 < 0 在同一条直线上，则 SKIPIF 1 < 0 的度数是 ．

45．（2023·山东济南·统考三模）公元三世纪，我国汉代数学家赵爽在注解《周髀算经》题时给出了“赵爽弦图”．将两个“赵爽弦图”（如图1）中的两个正方形和八个直角三角形按图2方式摆放围成正方形 SKIPIF 1 < 0 ，记空隙处正方形 SKIPIF 1 < 0 ，正方形 SKIPIF 1 < 0 的面积分别为 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则下列四个判断：① SKIPIF 1 < 0 ② SKIPIF 1 < 0 ；③若 SKIPIF 1 < 0 ，则 SKIPIF 1 < 0 ；④若点A是线段 SKIPIF 1 < 0 的中点，则 SKIPIF 1 < 0 ，其中正确的序号是

46．（2023·山东济宁·济宁学院附属中学校考三模）如图，从一个边长为 SKIPIF 1 < 0 的铁皮正六边形 SKIPIF 1 < 0 上，剪出一个扇形 SKIPIF 1 < 0 ．若将剪下来的扇形 SKIPIF 1 < 0 围成一个圆锥，则该圆锥的底面半径为 ．
47．（2023·河南周口·河南省淮阳中学校考三模）如图，在矩形 SKIPIF 1 < 0 中， SKIPIF 1 < 0 ，把边 SKIPIF 1 < 0 沿对角线 SKIPIF 1 < 0 平移，点 SKIPIF 1 < 0 分别对应点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的最小值为 ．

48．（2023·浙江杭州·校考二模）如图所示的五边形花环是用五个全等的等腰三角形拼成的，则∠BAC的度数为 ．
49．（2023·江苏盐城·景山中学校考三模）如图，在矩形ABCD中，AB＝13，BC＝17，点E是线段AD上一个动点，把△BAE沿BE向矩形内部折叠，当点A的对应点A1恰好落在∠BCD的平分线上时，AE的长为 ．
50．（2023·河南洛阳·统考三模）如图，将矩形纸片 SKIPIF 1 < 0 折叠，折痕为 SKIPIF 1 < 0 ，点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 分别在边 SKIPIF 1 < 0 ， SKIPIF 1 < 0 上，点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的对应点分别在 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，且点 SKIPIF 1 < 0 在矩形内部， SKIPIF 1 < 0 的延长线交边 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ， SKIPIF 1 < 0 交边 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ． SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，当点 SKIPIF 1 < 0 为 SKIPIF 1 < 0 三等分点时， SKIPIF 1 < 0 的长为 ．

51．（2023·福建福州·校考二模）如图，在平行四边形 SKIPIF 1 < 0 中，E为 SKIPIF 1 < 0 的中点，连接 SKIPIF 1 < 0 并延长交 SKIPIF 1 < 0 的延长线于点F，连接 SKIPIF 1 < 0 ，且 SKIPIF 1 < 0 ．判断四边形 SKIPIF 1 < 0 的形状并证明；
52．（2023·山东济宁·济宁学院附属中学校考三模）定义：长宽比为 SKIPIF 1 < 0 ：1（n为正整数）的矩形称为 SKIPIF 1 < 0 矩形．
下面，我们通过折叠的方式折出一个 SKIPIF 1 < 0 矩形，如图①所示．
操作1：将正方形 SKIPIF 1 < 0 沿过点B的直线折叠，使折叠后的点C落在对角线 SKIPIF 1 < 0 上的点G处，折痕为 SKIPIF 1 < 0 ．
操作2：将 SKIPIF 1 < 0 沿过点G的直线折叠，使点A，点D分别落在边 SKIPIF 1 < 0 ， SKIPIF 1 < 0 上，折痕为 SKIPIF 1 < 0 ，则四边形 SKIPIF 1 < 0 为 SKIPIF 1 < 0 矩形．
设正方形 SKIPIF 1 < 0 的边长为1，则 SKIPIF 1 < 0 ．
由折叠性质可知 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则四边形 SKIPIF 1 < 0 为矩形，∴ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ，∴四边形 SKIPIF 1 < 0 为 SKIPIF 1 < 0 矩形．
阅读以上内容，回答下列问题：
（1）在图①中，所有与 SKIPIF 1 < 0 相等的线段是 ， SKIPIF 1 < 0 的值是 ；
（2）已知四边形 SKIPIF 1 < 0 为 SKIPIF 1 < 0 矩形，模仿上述操作，得到四边形 SKIPIF 1 < 0 ，如图②，求证：四边形 SKIPIF 1 < 0 是 SKIPIF 1 < 0 矩形；
（3）将图②中的 SKIPIF 1 < 0 矩形 SKIPIF 1 < 0 沿用（2）中的方式操作3次后，得到一个“ SKIPIF 1 < 0 矩形”，则n的值是 ．

53．（2023·北京昌平·统考二模）《墨子·天文志》记载：“执规矩，以度天下之方圆.”度方知圆，感悟数学之美.如图，正方形 SKIPIF 1 < 0 的面积为4，以它的对角线的交点为位似中心，作它的位似图形 SKIPIF 1 < 0 ，若 SKIPIF 1 < 0 ，则四边形 SKIPIF 1 < 0 的外接圆的半径为（ ）

A． SKIPIF 1 < 0 B．2C． SKIPIF 1 < 0 D．4
54．（2023·江苏盐城·景山中学校考三模）如图，菱形ABCD中，∠B＝60°，AB＝3，则以AC为边长的正方形ACEF的面积为（ ）
A．9B．12C．15D．20
55.（2023·四川攀枝花·统考二模）用四根长度相等的木条制作学具，先制作图（1）所示的正方形 SKIPIF 1 < 0 ，测得 SKIPIF 1 < 0 ，活动学具成图（2）所示的四边形 SKIPIF 1 < 0 ，测得 SKIPIF 1 < 0 ，则图（2）中 SKIPIF 1 < 0 的长是（ ） SKIPIF 1 < 0

A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D． SKIPIF 1 < 0
56．（2023·江苏无锡·统考三模）若正多边形的一个外角的度数为45°，则这个正多边形是（ ）
A．正五边形B．正六边形C．正八边形D．正十边形
57．（2023·河北石家庄·石家庄市第四十中学校考二模）如图，把八个等圆按相邻两两外切摆放，其圆心连线构成一个正八边形，设正八边形内侧八个扇形（无阴影部分）面积之和为S1，正八边形外侧八个扇形（阴影部分）面积之和为S2，则 SKIPIF 1 < 0 =（ ）

A． SKIPIF 1 < 0 B． SKIPIF 1 < 0 C． SKIPIF 1 < 0 D．1
58．（2023·北京昌平·统考二模）一个正多边形的内角和是它的外角和的2倍，则这个正多边形是正 边形.
59．（2023·江苏盐城·景山中学校考三模）如图，在矩形ABCD中，AB＝13，BC＝17，点E是线段AD上一个动点，把△BAE沿BE向矩形内部折叠，当点A的对应点A1恰好落在∠BCD的平分线上时，AE的长为 ．
60．（2023·山东济南·统考三模）如图，折叠矩形纸片 SKIPIF 1 < 0 ，使点D落在 SKIPIF 1 < 0 边的点M处， SKIPIF 1 < 0 为折痕， SKIPIF 1 < 0 ， SKIPIF 1 < 0 ．则四边形 SKIPIF 1 < 0 面积的最小值是 ．

（1）作 SKIPIF 1 < 0 的垂直平分线交 SKIPIF 1 < 0 于点O；

（2）连接 SKIPIF 1 < 0 ，在 SKIPIF 1 < 0 的延长线上截取 SKIPIF 1 < 0 ；

（3）连接 SKIPIF 1 < 0 ， SKIPIF 1 < 0 ，则四边形 SKIPIF 1 < 0 即为所求．

瓦里尼翁平行四边形
我们知道，如图1，在四边形 SKIPIF 1 < 0 中，点 SKIPIF 1 < 0 分别是边 SKIPIF 1 < 0 ， SKIPIF 1 < 0 的中点，顺次连接 SKIPIF 1 < 0 ，得到的四边形 SKIPIF 1 < 0 是平行四边形．

我查阅了许多资料，得知这个平行四边形 SKIPIF 1 < 0 被称为瓦里尼翁平行四边形．瓦里尼翁 SKIPIF 1 < 0 是法国数学家、力学家．瓦里尼翁平行四边形与原四边形关系密切．

①当原四边形的对角线满足一定关系时，瓦里尼翁平行四边形可能是菱形、矩形或正方形．
②瓦里尼翁平行四边形的周长与原四边形对角线的长度也有一定关系．
③瓦里尼翁平行四边形的面积等于原四边形面积的一半．此结论可借助图1证明如下：
证明：如图2，连接 SKIPIF 1 < 0 ，分别交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，过点 SKIPIF 1 < 0 作 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ，交 SKIPIF 1 < 0 于点 SKIPIF 1 < 0 ．
∵ SKIPIF 1 < 0 分别为 SKIPIF 1 < 0 的中点，∴ SKIPIF 1 < 0 ．（依据1）

∴ SKIPIF 1 < 0 ．∵ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ．
∵四边形 SKIPIF 1 < 0 是瓦里尼翁平行四边形，∴ SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ．
∵ SKIPIF 1 < 0 ，即 SKIPIF 1 < 0 ，
∴四边形 SKIPIF 1 < 0 是平行四边形．（依据2）∴ SKIPIF 1 < 0 ．
∵ SKIPIF 1 < 0 ，∴ SKIPIF 1 < 0 ．同理，…