江西省九江市浔阳区第三中学2023-2024学年九年级上学期期中数学试题

这是一份江西省九江市浔阳区第三中学2023-2024学年九年级上学期期中数学试题，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本题共10小题，每小题3分，共30分）
1.下列方程中，是一元二次方程的是（ ）
A.B.C.D.
2.始于唐代的青花瓷给人以古朴、典雅之美.关于如图所示的青花瓷图案，下列说法正确的是（ ）
A.它是中心对称图形，但不是轴对称图形B.它是轴对称图形，但不是中心对称图形
C.它既是中心对称图形，又是轴对称图形D.它既不是中心对称图形，又不是轴对称图形
3.实验中学的初三篮球赛中，参赛的每两支球队之间都要进行一场比赛，共比赛21场，设参加比赛的球队有支，根据题意，下面列出的方程正确的是（ ）
A.B.C.D.
4.抛物线与轴的一个交点是，那么该抛物线与轴的另一个交点坐标是（ ）
A.B.C.D.
5.对二次函数的性质描述正确的是（ ）
A.该函数图象的对称轴在轴左侧B.当时，随的增大而减小
C.函数图象开口向下D.该函数图象与轴的交点位于轴负半轴
6.加工爆米花时，爆开且不煳的粒数的百分比称为“可食用率”，在特定条件下，可食用率与加工时间（单位：）满足函数表达式，则最佳加工时间为（ ）
A.B.C.D.
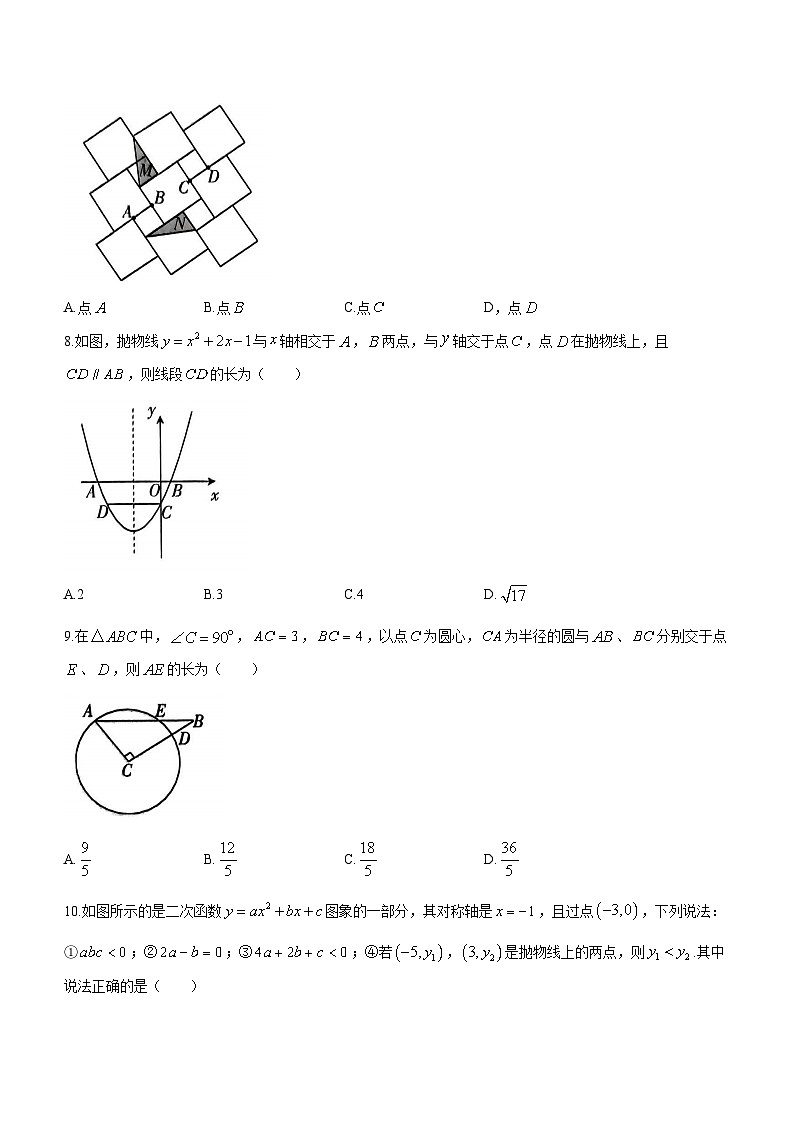
7.若干个正方形按如图所示的方式拼接，三角形经过旋转变换能得到三角形，下列四个点能作为旋转中心的是（ ）
A.点B.点C.点D，点
8.如图，抛物线与轴相交于，两点，与轴交于点，点在抛物线上，且，则线段的长为（ ）
A.2B.3C.4D.
9.在中，，，，以点为圆心，为半径的圆与、分别交于点、，则的长为（ ）
A.B.C.D.
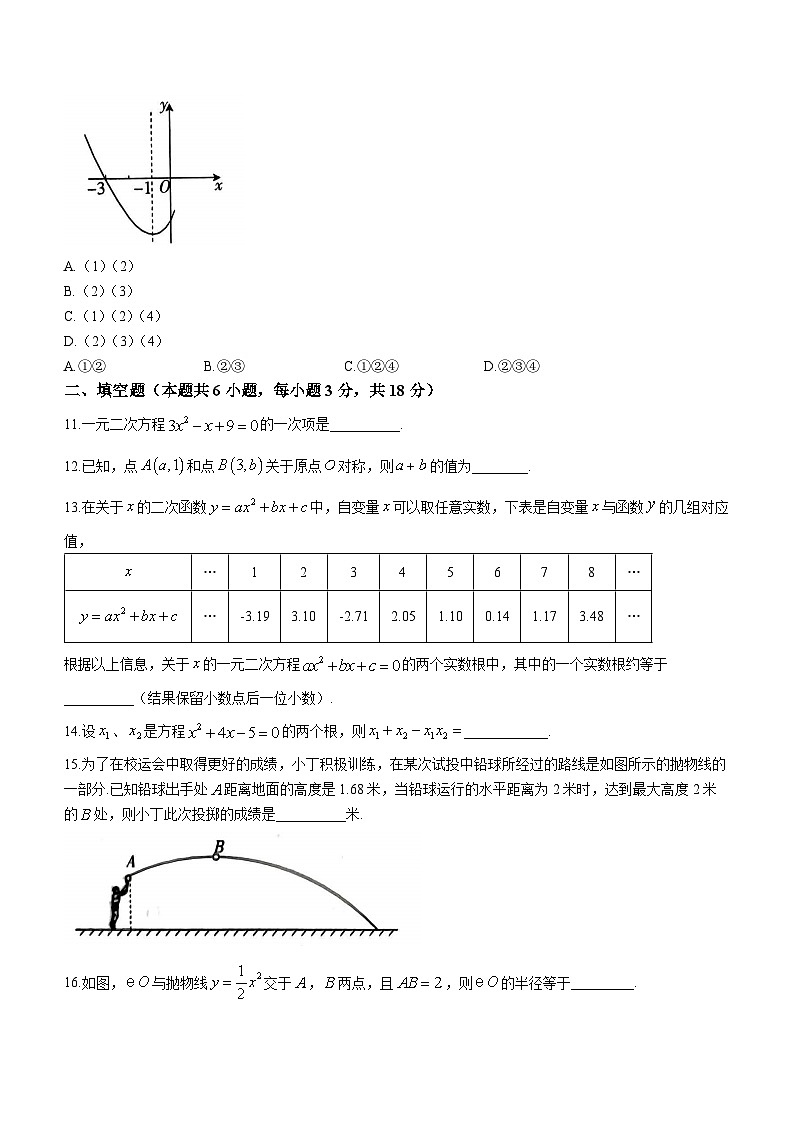
10.如图所示的是二次函数图象的一部分，其对称轴是，且过点，下列说法：①；②；③；④若，是抛物线上的两点，则.其中说法正确的是（ ）
A.（1）（2）
B.（2）（3）
C.（1）（2）（4）
D.（2）（3）（4）
A.①②B.②③C.①②④D.②③④
二、填空题（本题共6小题，每小题3分，共18分）
11.一元二次方程的一次项是__________.
12.已知，点和点关于原点对称，则的值为________.
13.在关于的二次函数中，自变量可以取任意实数，下表是自变量与函数的几组对应值，
根据以上信息，关于的一元二次方程的两个实数根中，其中的一个实数根约等于__________（结果保留小数点后一位小数）.
14.设、是方程的两个根，则____________.
15.为了在校运会中取得更好的成绩，小丁积极训练，在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处距离地面的高度是1.68米，当铅球运行的水平距离为2米时，达到最大高度2米的处，则小丁此次投掷的成绩是__________米.
16.如图，与抛物线交于，两点，且，则的半径等于_________.
三、解答题（本大题共9小题，共72分）
17.（6分）解下列方程：
（1）；（2）（请用配方法解）.
18.（6分）已知二次函数的图象经过点，.
（1）试确定此二次函数的解析式；
（2）请你判断点是否在这个二次函数的图象上.
19.（6分）如图，在中，.绕点逆时针旋转，旋转角为，点为点的对应点.
（1）请用尺规作图法画出旋转后的；
（2）若，，，求的长.
20.（6分）已知关于的一元二次方程有两个不相等的实数根.
（1）求的取值范围.
（2）当时，求出此时方程的两个根.
21.（8分）已知矩形的顶点、在圆上，、两点在圆内，请仅用没有刻度的直尺作图.
图1 图2
（1）如图1，已知圆心，请作出直线；
（2）如图2，未知圆心，请作出直线.
22.（8分）某超市需购进某种商品，每件的进价10元.设该商品的销售单价为（单位：元/件），在销售过程中发现：当时，该商品的日销售量（单位：件）与销售单价之间存在一次函数关系，，之间的部分数值的对应关系如下表：
（1）请求出当时，与之间的函数关系式；
（2）设该商品的日销售利润为元，当该商品的销售单价（元/件）定价为多少元时，日销售利润最大?最大利润是多少?
23.（10分）在中，，，将绕点顺时针旋转一个角度得到，点、的对应点分别是点、.
图1 图2
（1）如图1，若点恰好与点重合，，垂足为，求的大小；
（2）如图2，若，连接交于点，求证：四边形是平行四边形.
24.（10分）如图，在平行四边形中，，，边上的高，点是边上的动点，以为半径的与边交于点，（点在点的左侧）.
（1）当经过点时，求的长.
（2）连接，当时，求的半径及弦的长.
25.（12分）某数学兴趣小组在探究函数的图象和性质时，经历了以下探究过程.
（1）列表（完成下列表格）.
（2）描点并在图中画出函数的大致图象.
（3）根据函数图象，完成以下问题：
①当函数的图象向下平移__________个单位长度时，图象与轴有三个公共点；
②结合图象探究发现，当满足___________时，方程有四个解.
一、选择题
二、填空题
三、解答题
17.解：（1），.（3分）
（2），.（6分）
18.解：（1）；（3分）
（2）当时，，
点在这个二次函数的图象上（6分）
19.解：（1）如图，为所作；（3分）
（2）.（6分）
20.解：（1）根据题意得，解得；（3分）
（2），.（6分）
21.解：（1）如图1，直线为所求；（4分）
（2）如图2，直线为所求.（8分）
图1 图2
22.解：（1）；（4分）
（2）当该商品的销售单价定价为20元时，日销售利润最大，最大利润是1200元（8分）
23.解：（1）；（4分）
（2）证明略.（10分）
24.解：（1）5；（5分）
（2）的半径为，
.（10分）
25.解：（1）把，1分别代入函数表达式得，2；
故，；（2分）
（2）描点确定函数图象如下：（6分）
（3）①从图象看，当函数的图像向下平移3个单位长度时，图象与轴有三个公共点；（9分）
②从图象看，当时，方程有四个解.（12分）…
1
2
3
4
5
6
7
8
…
…
-3.19
3.10
-2.71
2.05
1.10
0.14
1.17
3.48
…
销售单价（元/件）
10
20
日销售是（件）
180
120
…
-3
-2
-1
0
1
2
3
…
…
6
3
2
3
3
6
…
1
2
3
4
5
6
7
8
9
10
C
B
B
B
A
B
C
A
C
A
11
12
13
14
15
16
-4
5.8
1
7