人教版八年级下册18.1.2 平行四边形的判定课前预习ppt课件

这是一份人教版八年级下册18.1.2 平行四边形的判定课前预习ppt课件，共19页。PPT课件主要包含了知识回顾，学习目标，对边相等，对角线互相平分，对角相等，课堂导入，新知探究，证明连接AC，∴ADBC，∴ABCD等内容，欢迎下载使用。
两条平行线之间的距离：两条平行线中，一条直线上任意一点到另一条直线的距离，叫做这两条平行线之间的距离.
性质：如果两条直线平行，那么一条直线上所有的点到另一条直线的距离都相等，即平行线间的距离处处相等.
1.探索并证明平行四边形的判定定理.2.能熟练运用平行四边形的判定定理去计算和证明.
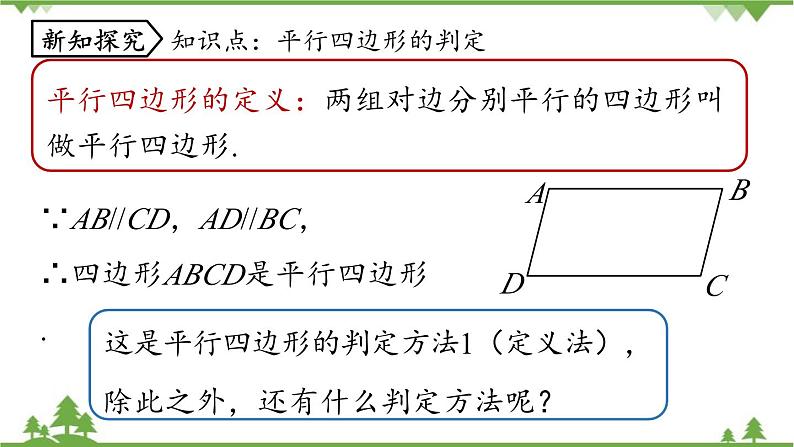
平行四边形的性质有哪些？
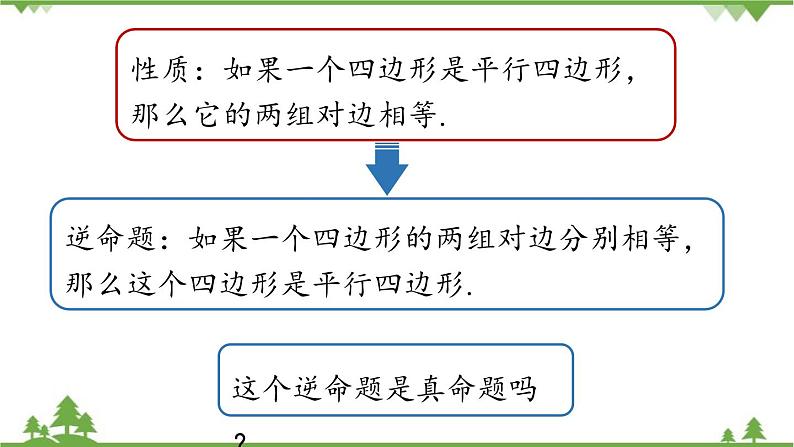
平行四边形的定义：两组对边分别平行的四边形叫做平行四边形.
∵AB//CD，AD//BC，∴四边形ABCD是平行四边形.
知识点：平行四边形的判定
性质：如果一个四边形是平行四边形，那么它的两组对边相等.
逆命题：如果一个四边形的两组对边分别相等，那么这个四边形是平行四边形.
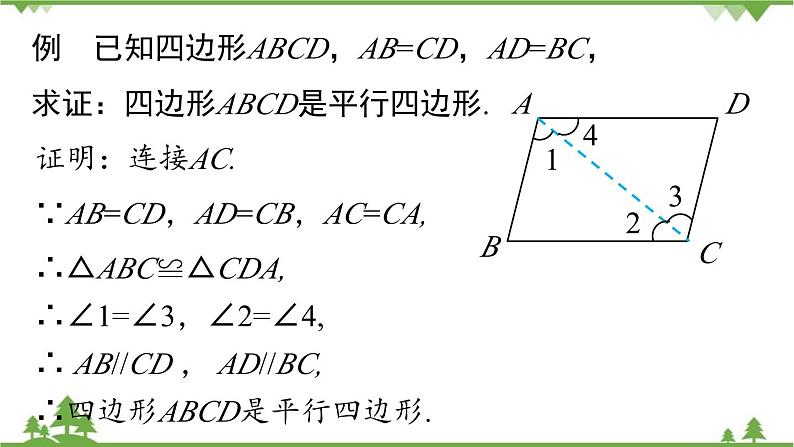
例 已知四边形ABCD，AB=CD，AD=BC，求证：四边形ABCD是平行四边形.
∵AB=CD，AD=CB，AC=CA,
∴ AB//CD ， AD//BC,
∴四边形ABCD是平行四边形.
∴△ABC≌△CDA,
∴∠1=∠3，∠2=∠4,
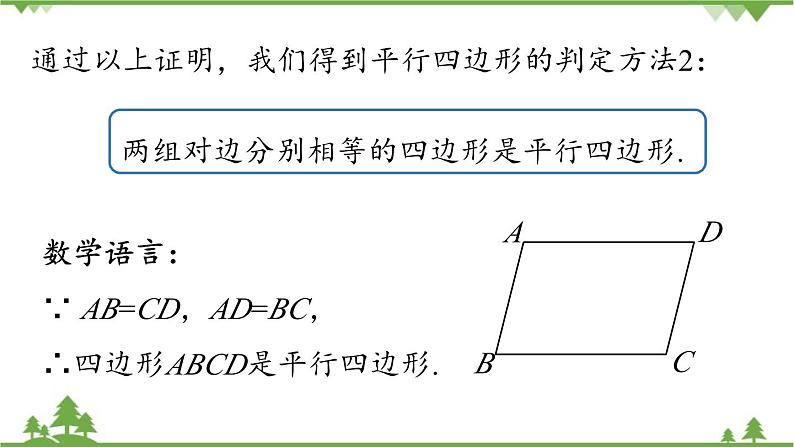
数学语言： ∵ AB=CD，AD=BC，∴四边形ABCD是平行四边形.
通过以上证明，我们得到平行四边形的判定方法2：
将两个含有30°角的直角三角板按如图所示摆放，则四边形ABCD是平行四边形，请说明理由.
解：∵ ∠ADB=∠CBD=30〫,
∵ ∠ABD=∠CDB=90〫,
∴四边形ABCD是平行四边形.
1.如图， 在四边形ABCD中， ∠1=∠2， ∠3=∠4，求证：四边形ABCD是平行四边形.
证明： ∵∠1=∠2，∠3=∠4，
∴ AB//CD ， AD//BC，
2.如图，在平行四边形ABCD中， BE=DF. 求证：四边形AECF是平行四边形.
证明：∵四边形ABCD是平行四边形
∴AB=CD， ∠B=∠D，
∴△ABE≌△CDF(SAS)，
∴∠AEB=∠CFD.
∵四边形ABCD是平行四边形，
∴四边形AECF是平行四边形.
∴AD//BC， ∠CFD=∠FCB，
∵ AE//CF，AF//CE，
3.如图，已知在四边形ABCD中，AE⊥BD于点E，CF⊥BD于点F，AE=CF，BF=DE，求证：四边形ABCD是平行四边形.
证明：∵AE⊥BD，CF⊥BD，
∴△ADE≌△CBF（SAS），
∴∠AED=∠CFB=90°.
∵DE=BF，AE=CF ，
∴△ABE≌△CDF（SAS），
∵BF=DE，∴BE=DF，
∵∠AEB=∠CFD=90°，且AE=CF，
∴四边形ABCD是平行四边形．
1.如图，AD⊥AC，BC⊥AC，且AD=BC. 求证：四边形ABCD是平行四边形.
证明：∵BC⊥AC , AD⊥AC ,
∴△ABC≌△CDA(SAS).
∴ ∠ACB=∠CAD=90°.
又∵ BC=AD , AC=CA,
2.如图，在三角形ABC中， AB=AC，点D是BC上任意一点，DE平行AC交AB于点E， DF平行AB交AC于点F. 求证：DE+DF=AC.