高中数学人教A版 (2019)选择性必修 第二册4.2 等差数列第2课时教学设计

这是一份高中数学人教A版 (2019)选择性必修 第二册4.2 等差数列第2课时教学设计，共6页。教案主要包含了教材内容微观分析，教学目标和教学重，教学环节阐释等内容，欢迎下载使用。
我今天说课的课题是：人教A版普通高中教科书数学选择性必修第二册第四章第二单元第四课时《等差数列的应用》。基于“理解数学、理解学生、理解教学、理解技术”的教育理论，从以下三方面进行教学说课：教材内容微观分析，教学目标和教学重难点的设置、教学环节阐释。
一、教材内容微观分析
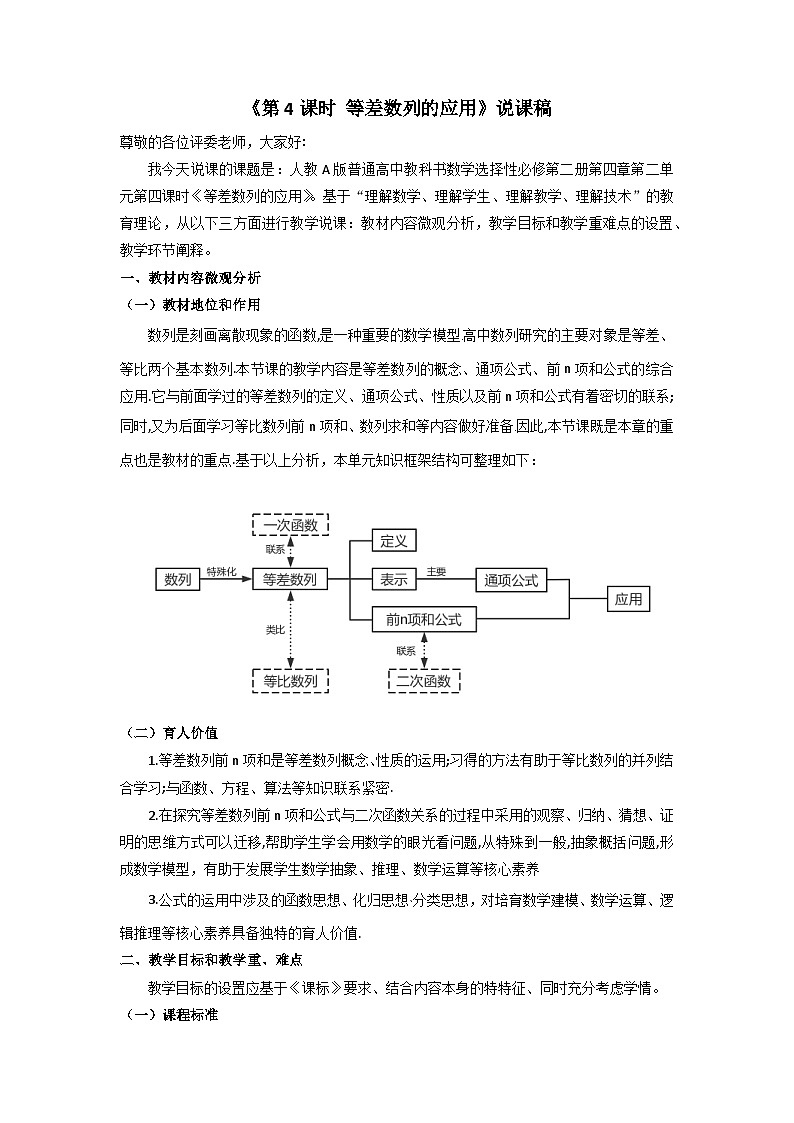
（一）教材地位和作用
数列是刻画离散现象的函数,是一种重要的数学模型﹒高中数列研究的主要对象是等差、等比两个基本数列.本节课的教学内容是等差数列的概念、通项公式、前n项和公式的综合应用.它与前面学过的等差数列的定义、通项公式、性质以及前n项和公式有着密切的联系;同时,又为后面学习等比数列前n项和、数列求和等内容做好准备﹒因此,本节课既是本章的重点也是教材的重点.基于以上分析，本单元知识框架结构可整理如下：
（二）育人价值
1.等差数列前n项和是等差数列概念、性质的运用;习得的方法有助于等比数列的并列结合学习;与函数、方程、算法等知识联系紧密.
2.在探究等差数列前n项和公式与二次函数关系的过程中采用的观察、归纳、猜想、证明的思维方式可以迁移,帮助学生学会用数学的眼光看问题,从特殊到一般,抽象概括问题,形成数学模型，有助于发展学生数学抽象、推理、数学运算等核心素养
3.公式的运用中涉及的函数思想、化归思想﹑分类思想，对培育数学建模、数学运算、逻辑推理等核心素养具备独特的育人价值.
二、教学目标和教学重、难点
教学目标的设置应基于《课标》要求、结合内容本身的特特征、同时充分考虑学情。
（一）课程标准
1.理解等差数列通向公式与前n项和公式的关系；
2.能在具体的问题情境重，发现数列的等差关系，并解决相应的问题。
（二）学情分析
数列是一类特殊的函数，学习路径和函数有相似之处。对于高二的学生，从知识结构上来看，在高一时经历了研究函数的一般路径，在知识、经验方面有所积累,并且学生通过前面的的学习，对等差数列的概念、通项公式以及前n项和公式学生也有了初步的理解,这些都为本课时的应用提供了探究方法和理论基础；在能力水平上方面，学生已经具备一定的抽象、推理、类比等能力，但公式的灵活应用能力不足、从实际情境中建立数学模型的能力还有待提升.
（三）教学目标与教学重、难点
通过上述综合分析，我制定了如下教学目标和教学重、难点：
1.目标解析：
（1）通过观察与联系，能够说明等差数列前n项和公式的代数特征，能够解释等差数列的通项公式与前n项和公式的内在联系，体会转化与化归纳的数学思想；
（2）通过数学问题情境，探索等差数学前n项和公式与二次函数的共性与区别，能够从函数角度解决求数列前n项和的最值问题，感受数学的整体性，体会函数思想、数形结合等数学思想方法，发展学生逻辑推理和数学运算素养；
（3）能将实际问题提炼成等差数列模型，识别等差数列的基本量，利用通向公式和前n项和公式解决问题，进一步体会转化与化归、方程思想，培育学生数学建模素养。
2.教学重、难点：
教学重点：等差数列通项公式、前n项和公式的应用.
教学难点：（1）从实际情境中发现等差数列现象；
（2）等差数列前n项和与二次函数的联系.
三、教学环节阐释
（一）教法分析
建构主义学习理论应认为：把学习看成是学生主动的建构活动.。因此，本节课设计以该理论指导思想，采用“诱思探究教学法”，在教学中采用以问题驱动,层层铺垫,由特殊到一般的方法启发学生,并采用例题和练习的形式加强公式的掌握运用﹒整个教学过程分成探究与发现、应用公式、方法归纳三个阶段.
（二）学法分析
在教学中,让学生在问题情境中,经历知识的形成和发展,通过观察、探索、反思、交流参与学习,认识和理解数学知识,学会学习,提升能力，发展数学核心素养.
（三）教学思路
环节一：复习导入
等差数列前n项和公式有哪几种形式？你能说出它们各自的使用范围吗？
教师引导学生回顾等差数列前n项和公式的两种形式及适用范围，有利于学生理解公式变化，认识变化的本质，让学生能在后续应用中根据不同的条件选用恰当的公式。
环节二：再探公式，构建联系
问题1：将公式（2）按项数n降幂排列，你有什么发现？
---（3），当时，可以看作常数项为0的二次函数
追问1：从结构上看，公式（3）有什么特点？
①常数项为0；②具有的形式；③二次项系数的2倍等于公差；
④二次项系数和一次项系数之和等于首相.
探究：等差数列的前n项和具有的形式，反之，更一般的情况：
如果数列的前n项和为，其中为常数且，那么这个数列一定是等差数列吗？
追问2：当时，计算出以及的值，你有什么发现？
追问3：当时，计算出以及的值，你有什么发现？
追问4：你能证明你的猜想吗？
（教师引导：①如何证明一个数列是等差数列；②已知前n项和如何求通项公式）
环节3：
本环节是本节课的一个难点.教师引导学生通过对公式进行变形，发现等差数列前n项和公式与二次函数的联系，进一步等差数列前n项和公式的函数特征，体会数学的整体性，形成分析代数表达式的一般思路，发展学生数学抽象素养；对于探究部分，教师通过3个追问为引导，学生经历从特殊到一般，使学生形成合理猜想并能严谨证明，培养学生辩证看待问题的思维方式，提升学生“四能”，发展学生逻辑推理素养.
环节三：运用公式，巩固理解
例1 某校新建一个报告厅，要求容纳80个座位，报告厅共有20排座位，从第二排起后一排都比前一排多两个座位.问第1排安排多少个座位.
追问5：用数学方法解决实际问题的一般步骤是什么？
追问6：从例1中，你能总结建立数列模型模型解决实际问题的基本步骤吗？
例2 已知一个等差数列的前项和为，若，公差，则是否存在最大值？若存在，求的最大值？若不存在，请说明理由.
追问7：你能利用函数思想，研究更一般的等差数列前n项和的最大（小）值吗？
①是否有最值，可以利用公式（3），结合数列的图象得出结论；
②如果有最值，对应的项数n是一个还是两个，关键要看中是否有一项为0，若有，则使得取得最值的n有两个；否则，n只有一个.
对于例1及追问5、6，教师引导学生分析问题，发现实际问题中的等差关系，从而将实际问题转化为等差数列前n项和的问题，即：“已知，求”，有利于促进学生灵活应用公式，进一步体会建立数列模型解决实际问题的思想方法，发展数学建模素养；对于例2及追问7，教师引导学生分析，学生独立选用两种方法解题，并进行展示交流，通过综合运用求和公式和函数的思想方法解决问题，探讨等差数列的单调性与最值的关系，进一步强化等差数列的前n项和公式与一元二次函数的联系，提高学生对数列与函数的共性与差异的认识.
环节四：课堂练习，内化公式
教科书第24页练习第1，2，3，4
学生独立解答，教师引导学生交流，师生互动补充完善，可检验学生对等差数列前n项和公式的掌握情况.
环节五：课堂小结，反思升华
回顾本节课学习内容，回答下列问题：
（1）求等差数列前n项和最大（小）值的方法有哪些？
（2）如何将实际问题转化为数学问题？
（3）本节课你体会到哪些思想方法？
通过学生回顾、归纳、总结，培养学生学以致用的学习意识，领会解决问题的思想方法，积累运用公式的基本活动经验，落实数学抽象、数学运算、逻辑推理和数学建模等核心素养.
环节六：分层作业，应用迁移
1.基础性作业
（1）必做题：教科书24-25页习题4.2第1、3、6、7、8题；
（2）选做题：教科书第24页练习第5题，第25页习题4.2第9题
2.拓展性作业
设是等差数列的前项和，已知.
（1）若，求的通项公式；
（2）若，求使得时的取值范围.
基础性作业主要考查学生对等差数列前n项和公式的理解程度，以及能否运用等差数列的性质解决问题.拓展性作业主要考查学生运用等差数列的通向公式和前n项和公式解决问题的能力.
（四）板书设计
板书要基本体现整堂课的内容与方法，体现课堂进程，能简明扼要反映知识结构及其相互联系；能指导教师的教学进程、引导学生探索知识；对于本节课，我采用地是关系式板书设计。同时可以通过使用幻灯片辅助板书，节省课堂时间，使课堂进程更加连贯。
（五）教学效果预测
通过本节，我预设如下教学效果：
1.通过观察与发现，能够说明等差数列前n项和公式的代数特征，能够解释等差数列的通项公式与前n项和公式的内在联系，体会转化与化归纳的数学思想；
2.通过具体问题探究，经历从特殊到一般的学习过程，能够理解等差数列前n项和与二次函数的关系，并能从函数角度解决等差数列前n项和的最值问题，发展学生逻辑推理、数学运算等核心素养.
3.深刻体会将实际问题转化为数学问题，并用相应的数学知识解决问题，体会数学的应用广泛性，发展学生数学抽象素养.
（六）课程资源开发与利用建议
（1）注重培养学生的自主学习习惯
教师可在课前为学生准备导学案，使学生带着问题进行自主预习，逐步形成能学习、会学习、善学习的优良态势；
（2）注重联系，突出转化，强化对等差数列的整体认识
本单元概念和公式为主，因此，在教学设计时不仅要注重概念公式的形成过程，更要注重公式之间的联系，注重公式与函数之间的联系，强化对等差数列的整体认识，体会数学的整体性.
（3）注重培育学生数学学科素养
每一个堂课都是发展学生核心素养的好契机。不论是从现实转化为数学、从特殊归纳为一般，或者是归纳小结形成知识框架等，都能发展学生数学抽象素养、逻辑推理、数学建模等核心素养；数学上大多数应用课都与运算有关，因此教科书设置了例题、练习和习题，教学时应引导学生注重依据定义、性质和进行求解，发展学生数学运算素养；
以上就是我对《等差数列的应用》这一节的认识和构想，不当之处，恳请各位专家批评指正。谢谢！