初中数学北师大版九年级上册第六章 反比例函数3 反比例函数的应用教学课件ppt

这是一份初中数学北师大版九年级上册第六章 反比例函数3 反比例函数的应用教学课件ppt，共14页。PPT课件主要包含了反比例函数的定义，复习回顾，增减性，一三象限，y随x的增大而增大，y随x的增大而减小，二四象限，归纳小结等内容，欢迎下载使用。

一般地，如果两个变量 x, y之间的关系可以表示成：
的形式，那么称 y 是 x 的反比例函数.
反比例函数的图象和性质：形状 反比例函数的图象是由两支曲线组成的.因此称反比例函数的图象为双曲线;位置 当 k > 0 时,两支曲线分别位于第一,三象限内;当 k < 0 时,两支曲线分别位于第二,四象限内;增减性 反比例函数的图象,当 k > 0 时,在每一象限内, y 随 x 的增大而减小; 当 k < 0 时,在每一象限内, y 随 x 的增大而增大.图象的发展趋势 反比例函数的图象无限接近于 x, y 轴,但永远达不到x, y 轴,画图象时,要体现出这个特点.对称性 反比例函数的图象是关于原点成中心对称的图形.任意一组变量的乘积是一个定值,即 xy = k.
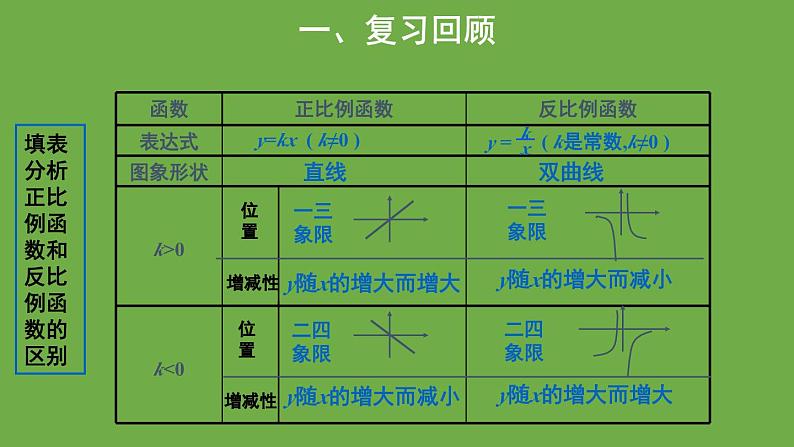
y=kx ( k≠0 )
双曲线
填表分析正比例函数和反比例函数的区别
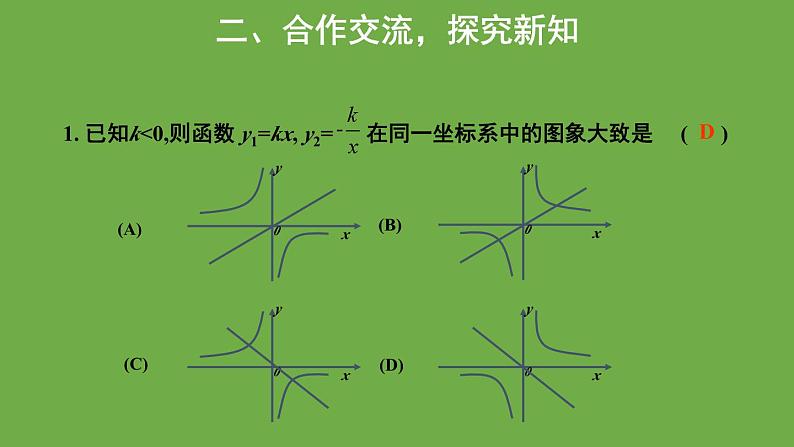
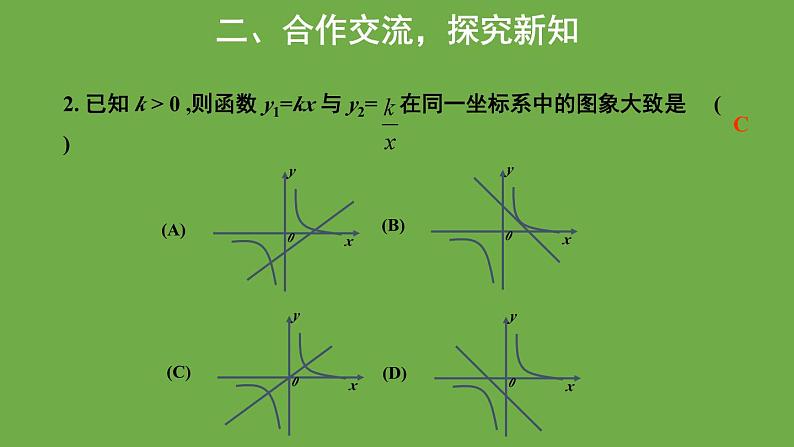
二、合作交流，探究新知
3. 设 x 为一切实数，在下列函数中，当 x 减小时，y 的值总是增大的函数是( )
4. 已知 y 与 x2 成反比例, 并且当 x = 3 时，y = 4.求 x = 1.5 时 y 的值.
解：设 x2y = k,因为 x = 3 时 y = 4所以 9×4= k所以 k = 36 当 x =1.5 时y =36÷（1.5×1.5）= 16
5. 设∆ABC 中 BC 边的长为 x（cm），BC上的高 AD 为 y（cm）. ∆ABC 的面积为常数,已知 y 关于 x 的函数图象过点（3，4）.
（1）求 y 关于 x 的函数解析式和∆ABC 的面积？
（2）画出函数的图象.并利用图象， 求当 2 < x < 8 时 y 的取值范围.
【思路点拨】延长 BA 与 y 轴相交于点 E，则S矩形ABCD=S矩形BEOC-S矩形AEOD.【自主解答】延长 BA 交 y 轴于点 E，由题意可得矩形AEOD 的面积为 1，矩形 BEOC 的面积为 3，所以矩形ABCD 的面积为 3-1=2.答案:2
（1）学习了反比例函数的应用；（2）在应用反比例函数解决问题时,一定要注意以下几点:①要注意自变量取值范围符合实际意义；②确定反比例函数之前一定要考察两个变量与定值之间的关系；若 k 未知时应首先由已知条件求出k值；③求“至少,最多”时可根据函数性质得到.