海南省海口市龙华区海南华侨中学2023届高三一模数学试题(含答案)

这是一份海南省海口市龙华区海南华侨中学2023届高三一模数学试题(含答案)，共17页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题
1、设全集,,,则( )
A.B.C.D.
2、设i为虚数单位,复数z满足,则( )
A.B.2C.D.1
3、若平面向量与满足,且,,则向量与的夹角为( )
A.B.C.D.
4、已知某圆台的高为,上底面半径为1,下底面半径为2,则其侧面展开图的面积为( )
A.9πB.C.D.
5、中国空间站的主体结构包括天和核心舱、问天实验舱和梦天实验舱.假设中国空间站要安排甲、乙、丙、丁4名航天员开展实验,其中天和核心舱安排2人,问天实验舱与梦天实验舱各安排1人,则甲、乙两人安排在不同舱内的概率为( )

A.B.C.D.
6、“”是“直线与曲线有交点”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
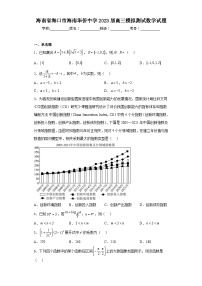
7、如图,抛物线的焦点为F,C的准线与x轴交于点A,过点F且斜率为的直线与C交于M（M在x轴上方）,N两点,则( )

A.3B.4C.D.6
8、关于函数,其中a,,给出下列四个结论：
甲：5是该函数的零点.
乙：4是该函数的零点.
丙：该函数的所有零点之积为0.
丁：方程有两个不等的实根.
若上述四个结论中有且只有一个结论错误,则该错误的结论是( )
A.甲B.乙C.丙D.丁
二、多项选择题
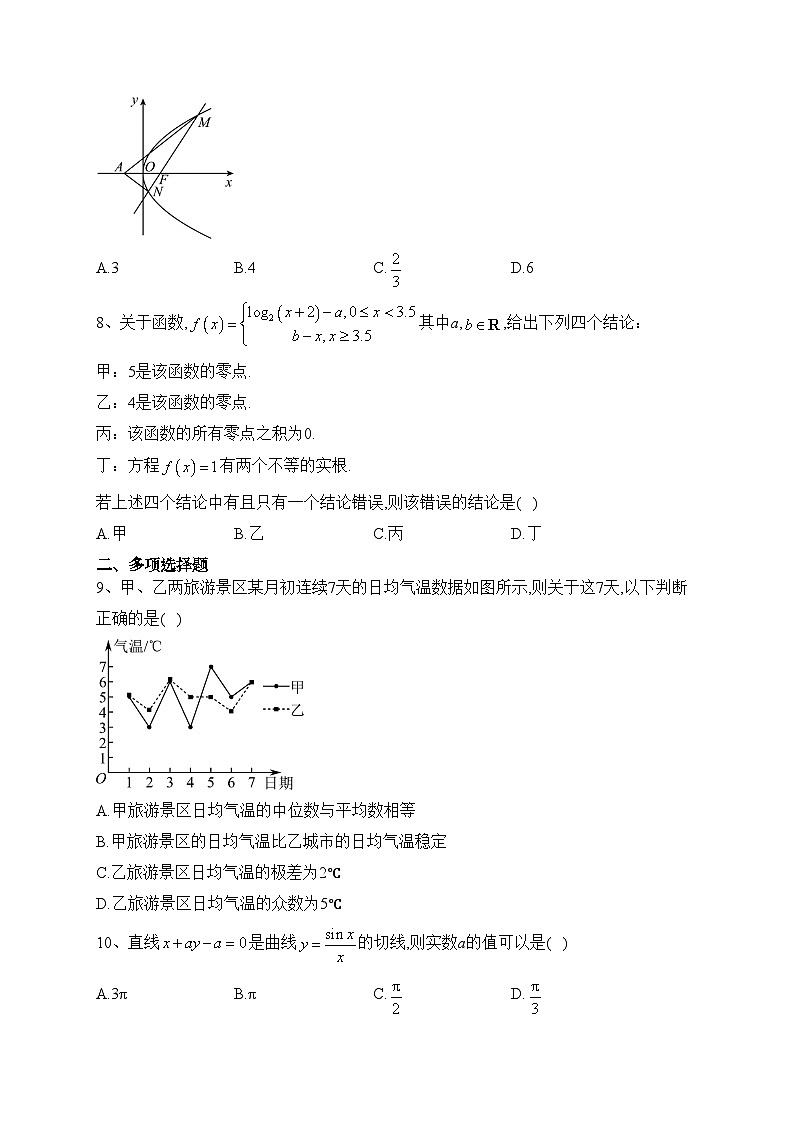
9、甲、乙两旅游景区某月初连续7天的日均气温数据如图所示,则关于这7天,以下判断正确的是( )
A.甲旅游景区日均气温的中位数与平均数相等
B.甲旅游景区的日均气温比乙城市的日均气温稳定
C.乙旅游景区日均气温的极差为2℃
D.乙旅游景区日均气温的众数为5℃
10、直线是曲线的切线,则实数a的值可以是( )
A.3πB.πC.D.
11、如图所示,该曲线W是由4个圆：,,,的一部分所构成,则下列叙述正确的是( )

A.曲线W围成的封闭图形面积为4+2π
B.若圆与曲线W有8个交点,则
C.与的公切线方程为
D.曲线W上的点到直线的距离的最小值为4
12、如图,在棱长为1的正方体中,Q是棱上的动点,则下列说法正确的是( )
A.不存在点Q,使得
B.存在点Q,使得
C.对于任意点Q,Q到的距离的取值范围为
D.对于任意点Q,都是钝角三角形
三、填空题
13、已知定义在R上的偶函数满足,且当时,,则________________.
14、在的展开式中,系数最大的项为_____________.
15、直径为4的球放地面上,球上方有一点光源P,则球在地面上的投影为以球与地面的切点F为一个焦点的椭圆.若椭圆的长轴为,垂直于地面且与球相切,,则椭圆的离心率为_____________.
16、如图,将绘有函数部分图象的纸片沿x轴折成直二面角,若此时A,B两点之间的空间距离为,则______________.

四、解答题
17、如图,在四棱锥中,底面ABCD是矩形,平面ABCD,,E,M分别为线段AB,PC的中点,连接CE,延长CE并与DA的延长线交于点F,连接PE,PF.
(1)求证：平面PFD.
(2)求平面APE与平面PEF所成角的正弦值.
18、在中,内角A,B,C的对边分别为a,b,c,且.
(1)求A的大小;
(2)若,,求BC边上高的长.
19、已知各项均为正数的数列满足,其中是数列的前n项和.
(1)求数列的通项公式;
(2)若对任意,且当时,总有恒成立,求实数的取值范围.
20、某公司有A,B两个餐厅为员工提供午餐与晚餐服务,甲、乙两名员工每天的午餐和晚餐都在公司就餐,近100天选择餐厅就餐情况统计如下：
假设甲、乙选择餐厅相互独立,用频率估计概率.
(1)记X为甲、乙两员工在一天中就餐餐厅的个数,求X的分布列和数学期望.
(2)假设M表示事件“A餐厅推出优惠套餐”,N表示事件“某员工去A餐厅就餐”, ,一般来说,在推出优惠套餐的情况下员工去该餐厅就餐的概率会比不推出优惠套餐的情况下去该餐厅就餐的概率要大,证明：.
21、已知函数.
(1)讨论函数的单调性;
(2)已知,若存在,不等式成立,求实数的最大值.
22、已知双曲线的右焦点为F,过点F的直线与双曲线C的两条渐近线分别交于A,B两点.
(1)若直线AB的斜率为1,求线段AB的中点坐标;
(2)若点,在双曲线C的右支上,且,,,过点P且斜率为的直线与过点Q且斜率为的直线交于线段AB上一点M,且,求实数的值.
参考答案
1、答案：D
解析：因为所以,
.
故选：D.
2、答案：A
解析： , .
故选：A.
3、答案：C
解析：设向量与的夹角为,则,解得,
因为, .
故选：C.
4、答案：A
解析：圆台的母线长为,
其侧面展开图的面积.
故选：A.
5、答案：B
解析：从甲,乙,丙,丁4名航天员中任选两人去天和核心舱,剩下两人去剩下两个舱位,则有种可能,
要使得甲乙在同一个舱内,由题意,甲乙只能同时在天和核心舱,在这种安排下,剩下两人去剩下两个舱位,则有种可能.
所以甲乙两人安排在同一个舱内的概率.
甲、乙两人安排在不同舱内的概率.
故选：B.
6、答案：B
解析：直线与曲线有交点,方程在上有解,
, ,
“”是“直线与曲线有交点”的必要不充分条件.
故选：B.
7、答案：D
解析： ,,直线MN的方程为,
联立方程,解得,.
点M在x轴上方,可得,,
.
故选：D.
8、答案：B
解析：当时,为减函数,故5和4只有一个是函数的零点.
即甲、乙中有一个结论错误,一个结论正确,故丙、丁均正确.
由所有零点之积为0,结合分段函数的性质,知必有一个零点为0,
则,可得.
①若甲正确,则,则,
可得
由,可得 或
解得或,方程有两个不等的实根,
故丁正确.,若甲正确,乙错误;
②若乙正确,则,即,则,
可得
由,可得,或,
解得,方程只有一个实根,故丁错误,不满足题意.
综上,甲正确,乙错误,
故选：B
9、答案：ACD
解析：甲旅游景区的气温分别为5℃,3℃,6℃,3℃,7℃,5℃,6℃;
乙旅游景区的气温分别为5℃,4℃,6℃,5℃,5℃,4℃,6℃.
甲旅游景区气温的中位数为5℃,平均数为,∴A项正确;
根据折线图知乙旅游景区的日均气温更稳定,B项错误;
乙旅游景区日均气温的极差为6－4=2℃,C项正确;
乙旅游景区日均气温的众数为5℃,D项正确.
故选：ACD.
10、答案：AB
解析：设切点为,直线恒过定点,
,,
, ,
,可取,
由导数的几何意义知,,
则,则,
所以,
当时,;当,,故A,B正确,C,D不正确.
故选：AB.
11、答案：ACD
解析：曲线W围成的封闭图形可分割为一个边长为2的正方形和四个半径为1的相同的半圆,
所以其面积为,故A选项正确.
当时,交点为B,D,F,H;当时,交点为A,C,E,G;
当或时,没有交点;当时,交点个数为8,故B选项错误.
设与的公切线方程为,
由直线和圆相切的条件可得,
解得,（舍去）,
则其公切线方程为,即,故C选项正确.
同理可得,的公切线方程为,
则两平行线的距离,故D选项正确.
故选：ACD.
12、答案：ABC
解析：由题知,在正方体中,Q是棱上的动点,建立以A为原点,
分别以,,的方向为x轴、y轴、z轴的正方向的空间直角坐标系.
所以,,,设,其中,
所以,,
当时,即,所以,显然方程组无解,
所以不存在使得,即不存在点Q,使得,故A项正确;
当时,解得,故B项正确;
因为,其中,所以点Q到的距离为
,
故C项正确;
因为,,其中,
所以,
所以三角形为直角三角形或钝角三角形,故D项错误.
故选：ABC.
13、答案：2
解析：,,即4为函数的周期,
.
故答案为：2.
14、答案：
解析：因为的通项为,的通项为,
展开式系数最大的项为,
展开式系数最大的项为,
在的展开式中,系数最大的项为.
故答案为：.
15、答案：
解析：依题意,平面截球O得球面大圆.
如图,是球O大圆的外切三角形,
其中,切圆O于点E,F,显然,
而,则,
又,则,
由圆的切线性质知.
在中,,则,于是得椭圆长轴长,
即.
又F为椭圆的一个焦点,令椭圆的半焦距为c,即,因此,
所以椭圆的离心率.
故答案为：.
16、答案：
解析：如图, 的周期,
,,

,解得,
,
由图可知,当,即,.
,
或.
观察函数在y轴右侧的图象结合正弦函数的单调性可知,
,
.
故答案为：.
17、答案：(1)证明见解析
(2) .
解析：（1）,且,
AE为的中位线,
ME为的中位线, .
又∵平面PFD,平面PFD,∴平面PFD.
（2）以A为坐标原点,分别以,,的方向为x,y,z轴的正方向建立空间直角坐标系,如图所示,则由已知可得,,,
∵x轴⊥平面PEA,∴设平面PEA的一个法向量为,平面PEF的法向量为,∵,,
,令,得,,,
,平面APE与平面PEF所成角的正弦值为.
18、答案：(1)
(2)
解析：（1）, ,
,
即.
又A,,,,.
（2）设BC边上的高为h,,
即,解得 ,
,解得,即BC边上的高为 .
19、答案：(1)
(2).
解析：（1）,
当时,,解得.
当时,,
即,
, ,
数列是以1为首项,2为公差的等差数列,
.
（2）因为,所以
当时, ,
,
,
实数的取值范围为.
20、答案：(1)分布列见解析,1.91
(2)证明见解析
解析：（1）由题知甲员工午餐、晚餐都选择A餐厅就餐的概率为0.4,都选择B餐厅就餐的概率为0.1;
乙员工午餐、晚餐都选择A餐厅就餐的概率为0.15,都选择B餐厅就餐的概率为0.3.
记X为甲、乙两员工在一天中就餐餐厅的个数,则X的所有可能取值为1,2,
,,
X的分布列为
X的数学期望.
（2）,
,,
,
,,
.
21、答案：(1)函数在,上单调递减
(2)
解析：（1）函数的定义域为,
所以,令,则,
函数在上单调递增,在上单调递减.
又,当时,,,
函数在,上单调递减.
（2）,且,,,
,, .
,由（1）知,函数在上单调递减,
只需在上能成立,
两边同时取自然对数,得,即在上能成立.
令,则,
当时,,函数在上单调递增,
当时,,函数在上单调递减,
,,
又, ,
实数的最大值为.
22、答案：(1)
(2)2
解析：（1）渐近线为,
由直线AB的斜率为1,点,得直线AB的方程为,
设,分别联立和,
可得,
设线段AB的中点坐标为,则,,
故线段AB的中点坐标为,
（2）设直线PQ的方程为,
则,解得,
,
, ,,
,.
设点则 ,
整理得,
, ,
解得.
又,,
,
,.
设直线AB的方程为,,,
则,解得,,
同理求得,,
,,
此时点M的坐标满足,,
解得,,
M为线段AB的中点,即,
实数的值为2.
选择餐厅情况（午餐,晚餐）
甲
40天
30天
20天
10天
乙
15天
35天
20天
30天
X
1
2
P
0.09
0.91