北师大版八年级下册2 直角三角形教学ppt课件

这是一份北师大版八年级下册2 直角三角形教学ppt课件，文件包含北师大版数学八年级下册12直角三角形第2课时同步课件pptx、北师大版数学八年级下册12直角三角形第2课时教学设计含教学反思docx等2份课件配套教学资源，其中PPT共17页， 欢迎下载使用。

探索并掌握判定直角三角形全等的“斜边、直角边”定理。
能够运用“HL”定理判定两个直角三角形全等，能够用数学语言清楚地表达自己的想法。
学会从数学的角度提出问题，理解问题，体验解决问题的多样性发展推理能力和创新精神。
“HL”定理的证明及应用。
掌握推理证明的方法，发展演绎推理能力。
思考1：判定两个三角形全等的方法有哪些？
思考2：满足下列条件的两个三角形是否全等?为什么?
1. 一个锐角及这个锐角的对边对应相等的两个直角三角形.
2. 一个锐角及这个锐角相邻的直角边对应相等的两个直角三角形.
3. 两直角边对应相等的两个直角三角形.
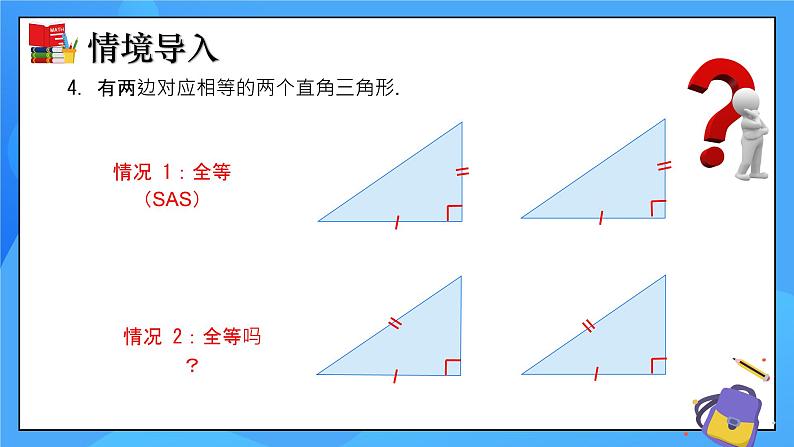
情况 1：全等（SAS）
4. 有两边对应相等的两个直角三角形.
已知一条直角边和斜边，求作一个直角三角形.
已知：如图，线段 a，c（a＜c），直角 α.
求作：Rt△ABC，使∠C =∠α，BC = a，AB = c.
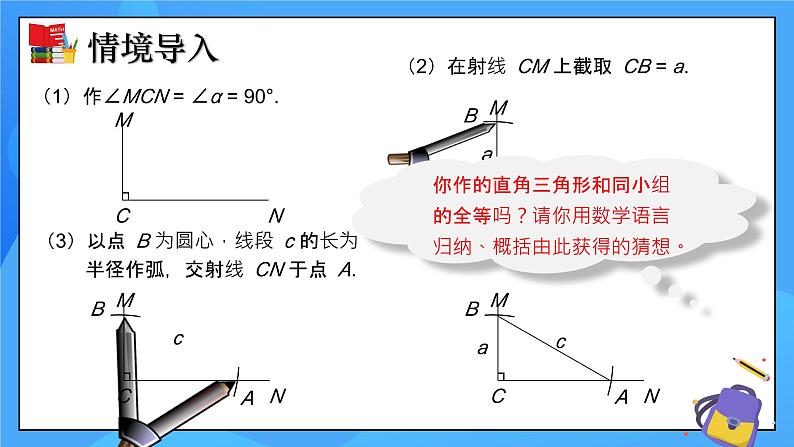
（1）作∠MCN = ∠α = 90°.
（2）在射线 CM 上截取 CB = a.
（3）以点 B 为圆心，线段 c 的长为 半径作弧，交射线 CN 于点 A.
（4）连接 AB，得到 Rt△ABC.
证明命题：斜边和一条直角边分别相等的两个直角三角形全等。
条件：斜边和直角边分别相等的两个直角三角形已知：如图，在△ABC 与△A'B'C' 中，∠C = ∠C' = 90°，AB = A'B’，AC = A'C'.
结论：两个直角三角形全等 求证：△ABC ≌ △A'B'C'.
证明：在△ABC 中，∵∠C = 90°，∴BC2 = AB2 – AC2（勾股定理）.同理，B'C'2 = A'B'2 – A'C‘2.又∵AB = A‘B’，AC = A‘C’，（已知）∴BC = B'C'.∴△ABC ≌ △A'B'C'（SSS）.
∵在Rt△ABC 与Rt△DEF 中， AB = DE，AC = DF. ∴△ABC ≌ △DEF（HL）
斜边和一条直角边对应相等的两个直角三角形全等.
只须找除直角外的两个条件即可（两个条件中至少有一个条件是一对对应边相等）
例：如图，有两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，两个滑梯的倾斜角∠B和∠F的大小有什么关系？
解：在Rt△ABC和Rt△DEF中,
∴ Rt△ABC≌Rt△DEF (HL).
∴∠B=∠DEF (全等三角形对应角相等).
∵ ∠DEF+∠F=90°,（直角三角形的两个锐角互余）
∴∠B+∠F=90°.（等量代换）
1.如图，AC⊥BC，BD⊥AD，要明证△ABC ≌ △BAD，需要添加一个什么条件？请说明理由．（1） （ ）；（2） （ ）；（3） （ ）；（4） （ ）．
∠DAB = ∠CBA
∠DBA = ∠CAB
2.已知：如图，AB=CD, BF⊥AC,DE⊥AC,AE=CF. 求证：BF=DE.
证明: ∵ BF⊥AC,DE⊥AC,（已知） ∴∠BFA=∠DEC=90 °.∵AE=CF，（已知） ∴AE+EF=CF+EF. 即AF=CE.在Rt△ABF和Rt△CDE中，
∴ Rt△ABF≌Rt△CDE (HL).
习题1.6第1、2、3题