





初中数学北师大版八年级下册2 直角三角形教学ppt课件
展开掌握直角三角形两个锐角互余,有两个角互余的三角形是直角三角形。结合具体实例,会区分命题的条件和结论,会识别两个互逆命题。
经历探索勾股定理及逆定理的证明过程,掌握一些推理方法,发展演绎推理的能力。
增强逆向思维的意识,体会辩证思想。发展演绎推理能力。
直角三角形中两个锐角的关系;勾股定理及逆定理的证明;识别逆命题和逆定理。
掌握推理证明的方法,发展演绎推理能力。
思考1:直角三角形的两个锐角有怎样的关系?为什么?
思考2:如果一个三角形有两个角互余,那么这个三角形是直角三角形吗?为什么?
请证明自己的结论,并与同伴交流.
直角三角形两个锐角互余。
有两个角互余的三角形是直角三角形。
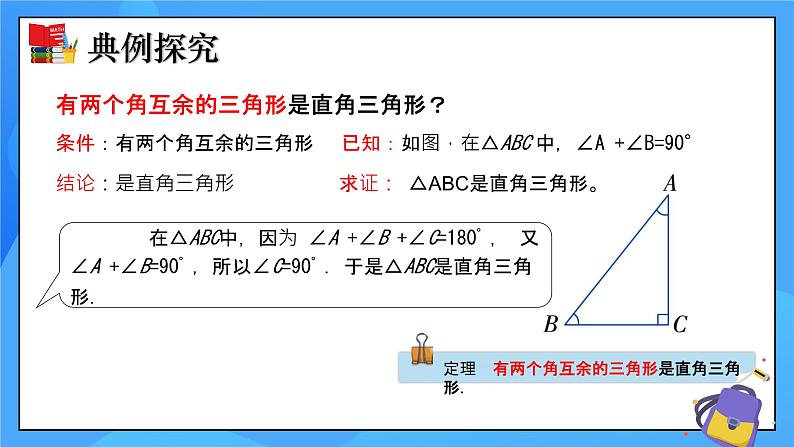
条件:有两个角互余的三角形 已知:如图,在△ABC 中,∠A +∠B=90°
结论:是直角三角形 求证: △ABC是直角三角形。
有两个角互余的三角形是直角三角形?
在△ABC中,因为 ∠A +∠B +∠C=180°, 又∠A +∠B=90°,所以∠C=90°. 于是△ABC是直角三角形.
∵在△ABC 中,∠A +∠B=90°(已知)∴△ABC是直角三角形。
思考4:反过来,在一个三角形中,当两边的平方和等于第三边 的平方时,我们曾用度量的方法得出“这个三角形是直角三角形”的结论.你能用基本事实和已经学习过的定理证明此结论吗?
思考3:我们前面曾利用数方格和割补图形的方法得到了勾股定理.
其实我们也可以用基本事实和已经学习过的定理证明此结论,这里作为课后研读,P16读一读。
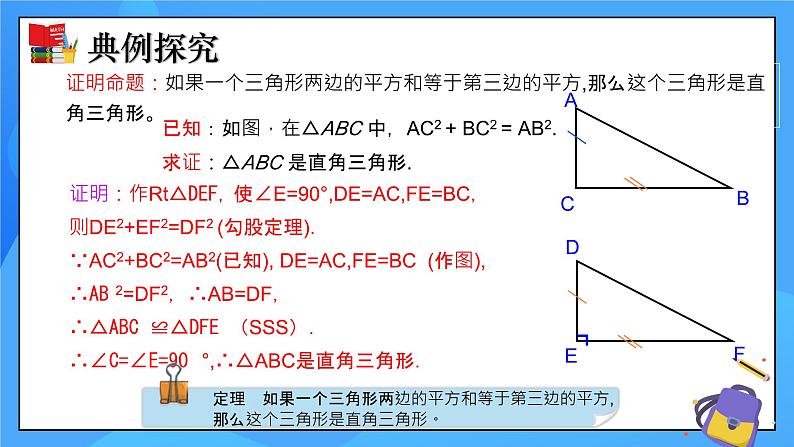
证明命题:如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
已知:如图,在△ABC 中,AC2 + BC2 = AB2.
求证:△ABC 是直角三角形.
证明:作Rt△DEF,使∠E=90°,DE=AC,FE=BC,则DE2+EF2=DF2 (勾股定理).∵AC2+BC2=AB2(已知), DE=AC,FE=BC (作图),∴AB2=DF2,∴AB=DF,∴△ABC≌△DFE(SSS).∴∠C=∠E=90°,∴△ABC是直角三角形.
∵ 在△ABC 中,AC2 + BC2 = AB2(已知)
∴△ABC 是直角三角形.
判断下列三边组成的三角形是不是直角三角形.
(1)a = 2,b = 3,c = 4. ( )
(2)a = 9,b = 7,c = 12. ( )
(3)a = 25,b = 20,c = 15. ( )
观察上面两个命题,它们的条件和结论之间有怎样的关系?在前面的学习中还有类似的命题吗? 上面两个定理的条件和结论互换了位置,即勾股定理的条件是第二个定理的结论,结论是第二个定理的条件.
如果两个角是对顶角,那么它们相等;如果两个角相等,那么它们是对顶角.
如果小明患了肺炎,那么他一定会发烧;如果小明发烧,那么他一定患了肺炎.
一个三角形中相等的边所对的角相等;一个三角形中相等的角所对的边相等.
在两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件,那么这两个命题叫做互逆命题.
如果把其中一个命题叫做原命题,那么另一个命题就叫做它的逆命题.
上面每两个命题的条件和结论恰好互换了位置.
命题“两直线平行,内错角相等”的条件和结论为:条件为:两直线平行;结论为:内错角相等.因此它的逆命题为:
内错角相等,两直线平行.
每一个命题都有逆命题,只要将原命题的条件改成结论,并将结论改成条件,便可得到原命题的逆命题.但是原命题正确,它的逆命题未必正确. 例如真命题“对顶角相等”的逆命题为“相等的角是对顶角”,此命题就是假命题.
如果一个定理的逆命题也是定理,那么这两个定理叫做互逆定理,其中的一个定理叫做另一个定理的逆定理.
注意1:逆命题、互逆命题不一定是真命题, 但逆定理、互逆定理,一定是真命题.
注意2:不是所有的定理都有逆定理.
1. 说出下列命题的逆命题,并判断每对命题的真假:
(1)四边形是多边形;(2)两直线平行,同旁内角互补;(3)如果 ab = 0,那么 a = 0,b = 0.
解:(1)多边形是四边形.原命题是真,逆命题是假. (2)同旁内角互补,两直线平行.原命题是真,逆命题是真. (3)如果那么 a = 0,b = 0,那么 ab = 0.原命题是假,逆命题是真.
1. 一个零件的形状如图所示,工人师傅量得这个零件各边尺寸如下(单位:dm):AB = 3,AD = 4,BC = 12,CD = 13.且∠DAB = 90°.你能求出这个零件的面积吗?
解:如图,连接 BD. 在Rt△ABD 中,
在△BCD 中,BD2 + BC2 = 52 + 122 = 132 = CD2.
∴△BCD 是直角三角形,∠DBC = 90°.
北师大版八年级下册4 分式方程集体备课课件ppt: 这是一份北师大版八年级下册4 分式方程集体备课课件ppt,共26页。PPT课件主要包含了什么叫方程,什么叫方程的解,分母中都含有未知数,方程的分母中含未知数,整式方程,分式方程,归纳总结,分式方程的概念,分式方程的特征,是分式但不是方程等内容,欢迎下载使用。
初中数学北师大版八年级下册1 认识分式教学ppt课件: 这是一份初中数学北师大版八年级下册1 认识分式教学ppt课件,文件包含北师大版数学八年级下册51认识分式第1课时同步课件pptx、北师大版数学八年级下册51认识分式第1课时教学设计含教学反思docx等2份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
北师大版八年级下册3 公式法教学ppt课件: 这是一份北师大版八年级下册3 公式法教学ppt课件,文件包含北师大版数学八年级下册43公式法第1课时同步课件pptx、北师大版数学八年级下册43公式法第1课时教学设计含教学反思docx等2份课件配套教学资源,其中PPT共24页, 欢迎下载使用。














