初中数学沪教版 (五四制)七年级上册10.5 可以化成一元一次方程的分式方程教学设计及反思

这是一份初中数学沪教版 (五四制)七年级上册10.5 可以化成一元一次方程的分式方程教学设计及反思，共5页。

课题名称
10.5可化为一元一次方程的分式方程
授课时间
课型
主备课人
新授课
教学目标制定依据
学情分析
教材分析
授课对象是七一班，女生19人，男生22人。女生的学习习惯较强，而男生的思维要比女生来的出色，但写字规范性和解题格式正确性还有待提高；班级数学整体处于中等水平，目前在数学学习方面的最大问题就是数学语言的表达能力较弱，上课的积极性也有待提高。
针对这些问题，教师在平时授课过程中要勇于让更多的学生表达自己的想法，在平时批改作业的过程中，要及时纠正学生不良习惯。
本节课是可化为一元一次方程的分式方程，是在学习分式的基本性质和分式计算的基础上展开讨论的，这是不同于解以前学习的方程的新问题。解分式方程用的是化归思想，分式方程一般要先化为整式方程再求解，注意验根是必不可少的步骤。
本节课的引入安排了实际生活中的例子，更贴近学生的实际，在学生讨论时，注意结合分析、解决实际问题的逐步深入。在讨论分式方程的解法时，从分析分式方程的特点入手，引出解分式方程的基本思路，即通过去分母使分式方程化为整式方程，再解出未知数。这里解分式方程的基本思路是很自然、很合理地产生的，这种处理既突出了分式方程解法上的特点及其算理，又反映了整式方程与分式方程在解法上的内在联系。在讨论增根问题时，通过具体例子展现了解分式方程时可能出现增根的现象，并结合例子分析了什么情况下产生增根，然后归纳出验根的方法。
教学环节
课前预习，完成预习学案————教师批阅
课堂反馈，完成课堂学案————教师授课
课后作业，完成练习册等————教师批阅及反馈
课堂
学习目标
技能与目标： 理解分式方程的意义，会按一般步骤解可化为一元一次方程的分式方程；
过程与方法： 通过实践与对比的方式，了解增根产生的原因，知道解分式方程须验根并掌握验根的方法.
情感价值态度观：通过学习解分式方程的思想，让学生知道“转化”的数学思想，提高学生数学概括能力。
重点难点
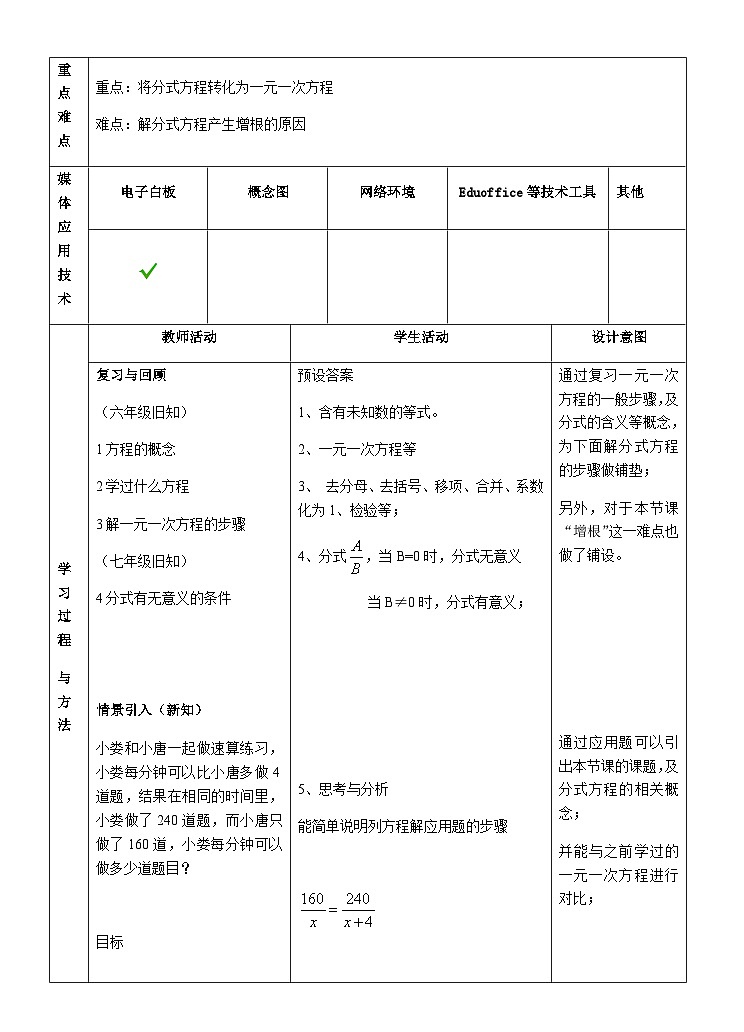
重点：将分式方程转化为一元一次方程
难点：解分式方程产生增根的原因
媒体应用技术
电子白板
概念图
网络环境
Eduffice等技术工具
其他
学习过程
与方法
教师活动
学生活动
设计意图
复习与回顾
（六年级旧知）
1方程的概念
2学过什么方程
3解一元一次方程的步骤
（七年级旧知）
4分式有无意义的条件
情景引入（新知）
小娄和小唐一起做速算练习，小娄每分钟可以比小唐多做4道题，结果在相同的时间里，小娄做了240道题，而小唐只做了160道，小娄每分钟可以做多少道题目？
目标
1根据题意，建立等量关系
2引导学生建立分式方程
3理解分式方程的含义
4辨析分式方程与整式方程
新知探索
1、观察分式方程
思考解分式方程的基本步骤
提出“转化”的思想
3、提示学生检验结果的正确性
（提问：检验是否一定需要。）
4、小结：解分式方程的步骤
深化新知
例1：解方程
例2：解方程
引出增根的含义
例2的结果使分式无意义，即分式方程无解。
问题1：增根产生的原因？
提示：
1、观察方程的结果和方程中分式的分母，发现什么？
分式方程本身隐藏的条件是什么？
3、分式方程转化为整式方程后，方程的取值范围扩大。
问题2：检验分式方程的解，除了代入原方程外，还可以代入哪里？
对于解可化为一元一次方程的分式方程的步骤进行总结；

层层深入
例3解方程：
解方程：
解方程：
解方程：
提高（选做）若分式方程：
的解x=，a=_______?
预设答案
1、含有未知数的等式。
2、一元一次方程等
3、 去分母、去括号、移项、合并、系数化为1、检验等；
4、分式，当B=0时，分式无意义
当B≠0时，分式有意义；
思考与分析
能简单说明列方程解应用题的步骤
预设答案：
能设元及建立分式方程；
分式方程：分母中含有未知数的方程
对比整式方程，完成相应判断题（ppt）
预设答案：1、去分母
2、用“比例”的方法
注意：本质还是去分母的思想。
3、分式方程通过去分母转化为整式方程（一元一次方程）
独立完成、板书演示
对比例题，发现问题
3、通过预习，引导学生给出增根的含义
小组讨论
回答
小组讨论
回答
注意解题格式
通过复习一元一次方程的一般步骤，及分式的含义等概念，为下面解分式方程的步骤做铺垫；
另外，对于本节课“增根”这一难点也做了铺设。
通过应用题可以引出本节课的课题，及分式方程的相关概念；
并能与之前学过的一元一次方程进行对比；
通过师生，生生交流明确本节课的第一个知识难点：去分母，也就是要找出最简公分母。提示学生检验，为下文引出增根做好铺垫。
根据教师的板书，注意格式，解题步骤等；提高学生的学习积极性。
对于分式方程，当分式中，分母的值为零时，无意义，所以分式方程，不允许未知数取那些使分母的值为零的值，即分式方程本身就隐含着分母不为零的条件。当把分式方程转化为整式方程以后，这种限制取消了，换言之，方程中未知数的值范围扩大了，如果转化后的整式方程的根恰好是原方程未知数的允许值之外的值，那么就会出现增根。
课堂小结
这节课学到了什么？
1解可化为一元一次方程的分式方程的步骤
2增根产生的原因等；
作业布置
完成练习册
课后反思
见附页