初中数学人教版八年级上册第十三章 轴对称13.3 等腰三角形13.3.2 等边三角形达标测试

这是一份初中数学人教版八年级上册第十三章 轴对称13.3 等腰三角形13.3.2 等边三角形达标测试，共10页。试卷主要包含了判断下列说法是否正确，已知等内容，欢迎下载使用。
1、判断下列说法是否正确：
1）直角三角形中30°角所对的直角边等于另一直角边的一半．（ ）
2）三角形中30°角所对的边等于最长边的一半。（ ）
3）直角三角形中较短的直角边是斜边的一半。（ ）
4）直角三角形的斜边是30°角所对直角边的2倍．（ ）
2、如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，CD是斜边AB上的高，AD＝3cm，则AB的长度是( )
A．3cm B．6cm C．9cm D．12cm
如图，∠AOP＝∠BOP＝15°，PC∥OA交OB于C，PD⊥OA于D，若PC＝3，则PD等于( )
A．3 B．2 C.1.5 D．1
4、如图，在△ABC中，∠C＝90°，AD是∠BAC的平分线，过点D作DE⊥AB.DE恰好是∠ADB的平分线．CD与DB有怎样的数量关系？请说明理由．
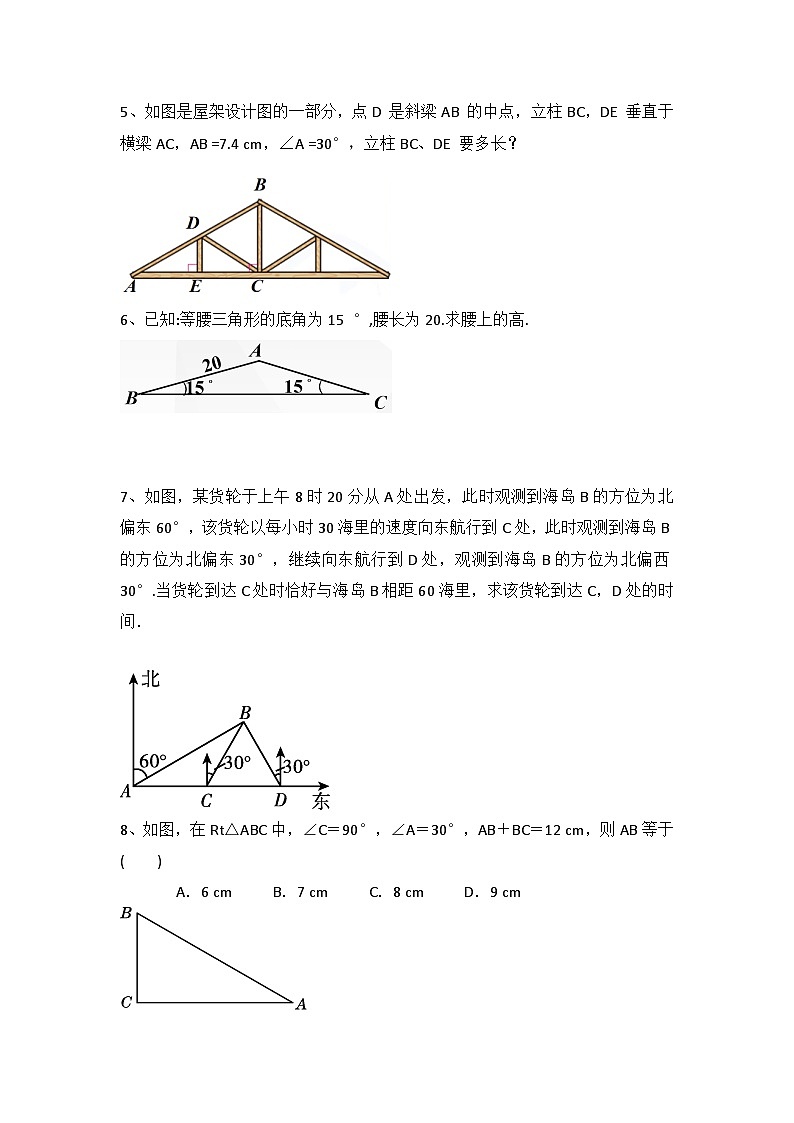
5、如图是屋架设计图的一部分，点D 是斜梁AB 的中点，立柱BC，DE 垂直于横梁AC，AB =7.4 cm，∠A =30°，立柱BC、DE 要多长？
6、已知:等腰三角形的底角为15 °,腰长为20.求腰上的高.
7、如图，某货轮于上午8时20分从A处出发，此时观测到海岛B的方位为北偏东60°，该货轮以每小时30海里的速度向东航行到C处，此时观测到海岛B的方位为北偏东30°，继续向东航行到D处，观测到海岛B的方位为北偏西30°.当货轮到达C处时恰好与海岛B相距60海里，求该货轮到达C，D处的时间．
8、如图，在Rt△ABC中，∠C＝90°，∠A＝30°，AB＋BC＝12 cm，则AB等于( )
A．6 cm B．7 cm C．8 cm D．9 cm
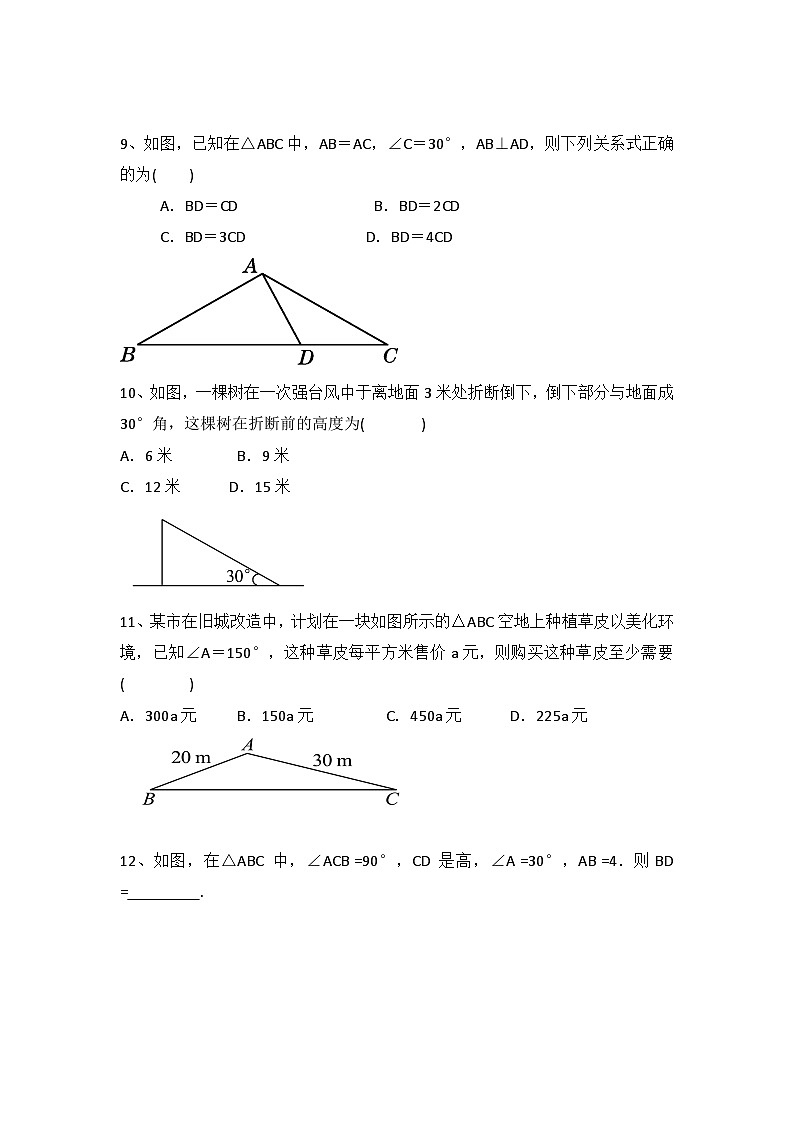
9、如图，已知在△ABC中，AB＝AC，∠C＝30°，AB⊥AD，则下列关系式正确的为( )
A．BD＝CD B．BD＝2CD
C．BD＝3CD D．BD＝4CD
10、如图，一棵树在一次强台风中于离地面3米处折断倒下，倒下部分与地面成30°角，这棵树在折断前的高度为( )
A．6米 B．9米
C．12米 D．15米
11、某市在旧城改造中，计划在一块如图所示的△ABC空地上种植草皮以美化环境，已知∠A＝150°，这种草皮每平方米售价a元，则购买这种草皮至少需要( )
A．300a元 B．150a元 C．450a元 D．225a元
12、如图，在△ABC 中，∠ACB =90°，CD 是高，∠A =30°，AB =4．则BD = .
13、在△ABC中,∠A: ∠B: ∠C=1:2:3,若AB=10,则BC = .
14、如图，Rt△ABC中，∠A= 30°，AB+BC=12cm，则AB=______.
15、在△ABC中，∠C=90°，∠B=15°，DE是AB的垂直平分线，BE=5，则求AC的长．
16、在△ABC中 ，AB=AC，∠BAC=120° ，D是BC的中点，DE⊥AB于E点，求证：BE=3EA.
17、如图，已知△ABC是等边三角形，D,E分别为BC、AC上的点，且CD=AE，AD、BE相交于点P，BQ⊥AD于点Q,求证:BP=2PQ.
18、如图，在 △ABC 中， ∠B=30∘ ， BC 的垂直平分线交 AB 于点 E ，垂足为 D ， CE 平分∠ACB .若 BE=8 ，则AE的长为( )
A. 4.5B. 5.5C. 4 D. 3.5
19、如图，在 △ABC 中， AB=AC ， ∠BAC=120∘，AD⊥AC 交 BC 于点 D .求证： BC=3AD .
20、含 30∘ 角的直角三角板与直线 L1 ， L2 的位置如图所示.已知 L1//L2 ， ∠A=30∘ ， ∠1=60∘ .若 AB=6 ，则 CD 的长为___.
21、如图，已知 ∠AOB=60∘，点P在边 OA 上，OP=12 ，点 M ，N 在边 OB 上，PM=PN .若MN=2，则OM= ( )
A. 3 B. 4 C. 5 D. 6
22、如图，灯塔 C 在海岛 A 北偏东 75∘ 方向上，某天上午8时，一艘船从海岛 A 出发，以15海里/时的速度由西向东航行，10时整到达 B 处，此时测得灯塔 C 在 B 处北偏东 60∘方向上.
B 处到灯塔 C 的距离为____海里.
（2）已知在以灯塔 C 为中心，周围16海里的范围内均有暗礁，若该船继续由西向东航行，是否有触礁危险？请说明理由.
23、如图，在四边形 ABCD 中， AD=4 ， BC=1 ， ∠A=30∘ ， ∠B=90∘ ， ∠ADC=120∘，则CD的长为___.
30°的直角三角形专项练习题答案
×，×，×，√
D
C
解：CD=DB
理由如下：∵DE⊥AB，
∴∠AED＝∠BED＝90°.∵DE是∠ADB的平分线，
∴∠ADE＝∠BDE.
又∵DE＝DE，
∴△AED≌△BED(ASA)，
∴AD＝BD，∠DAE＝∠B.
∵∠BAD＝∠CAD＝∠BAC，
∴∠BAD＝∠CAD＝∠B.
∵∠BAD＋∠CAD＋∠B＝90°，
∴∠B＝∠BAD＝∠CAD＝30°.
在Rt△ACD中，∵∠CAD＝30°，
∴CD＝AD＝BD，即CD＝DB.
解：∵DE⊥AC,BC ⊥AC, ∠A=30 °，
∴BC=AB, DE=AD.
∴BC=AB=×7.4=3.7(m).
又AD=AB,
∴DE=AD=×3.7=1.85 (m).
答：立柱BC的长是3.7m，DE的长是1.85m.
解:过C作CD⊥BA,交BA的延长线于点D.
∵∠B=∠ACB=15° (已知),
∴∠DAC=∠B+∠ACB= 15°+15°=30°，
∴CD=AC=×20=10.
解：由已知，
得∠BAC＝90°－60°＝30°，
∠ACB＝90°＋30°＝120°，
∠BCD＝∠BDC＝60°，
∴∠ABC＝∠BCD－∠BAC＝30°，
∠CBD＝180°－∠BCD－∠BDC＝60°，
∴∠ABC＝∠BAC＝30°，
∴AC＝BC＝60 海里，
∴货轮从A处到C处所需时间为60÷30＝2(小时)．
∵∠CBD＝∠BCD＝∠BDC ＝60°，
∴△BCD是等边三角形，
∴CD＝BC＝60海里，
∴货轮从C处到D处所需时间为60÷30＝2(小时)，
∴货轮 从A处到D处所需时间为2＋2＝4(小时)．
答：该货轮到达C处的时间是上午10时20分，到达D处的时间是中午12时20分．
C
B
B
B
1
5
8
解：连接AE，
∵DE是AB的垂直平分线，
∴BE=AE，
∴∠EAB=∠B=15°，
∴∠AEC=∠EAB+∠B=30°．
∵∠C=90°，
∴AC=AE=BE=2.5．
证明：∵AB=AC，∠BAC=120°， ∴∠B=∠C=30°.
∵ D是BC的中点，∴AD⊥BC
∴∠ADC=90°，∠BAD=∠DAC=60°.
∴AB=2AD.
∵DE⊥AB，∴∠AED=90°，
∴∠ADE=30°，∴AD=2AE.
∴AB=4AE，∴BE=3AE.
证明：∵△ABC为等边三角形，
∴ AC=BC=AB ,∠C=∠BAC=60°，
∵CD=AE，
∴△ADC≌△BEA.
∴∠CAD=∠ABE.
∵∠BAP+∠CAD=60°，∴∠ABE+∠BAP=60°.
∴∠BPQ=60°.
又∵ BQ⊥AD，
∴∠BQP=90°，
∴∠PBQ=30°，
∴BP=2PQ.
C
证明： ∵AB=AC ， ∠BAC=120∘ ，
∴∠B=∠C=30∘. ∵AD⊥AC ， ∴∠DAC=90∘. ∴CD=2AD ，
∠BAD=∠B=30∘. ∴AD=BD .
∴BC=CD+BD=3AD .
3
C
（1）30
（2）
解：有触礁危险.理由：过点 C 作 CD⊥AB 交 AB 的延长线于点 D .
∵∠CBD=90∘−60∘=30∘ ，
∠CAB=90∘−75∘=15∘ ， ∠CBD=∠ACB+∠CAB ，
∴∠CAB=∠ACB=15∘. ∴BC=AB=15×2=30 （海里） .
∴ 在 Rt△BCD 中， CD=1/2BC=15 海里 . ∵15