初中数学湘教版九年级上册4.3 解直角三角形精品课后作业题

这是一份初中数学湘教版九年级上册4.3 解直角三角形精品课后作业题，文件包含专题14模型构建专题解直角三角形应用中的基本模型压轴题六种模型全攻略原卷版docx、专题14模型构建专题解直角三角形应用中的基本模型压轴题六种模型全攻略解析版docx等2份试卷配套教学资源，其中试卷共41页， 欢迎下载使用。

目录
TOC \ "1-3" \h \u \l "_Tc10838" 【典型例题】 PAGEREF _Tc10838 \h 1
\l "_Tc24713" 【类型一 含特殊角（“30°，45°，60°”）的非直角三角形】 PAGEREF _Tc24713 \h 1
\l "_Tc29084" 【类型二 不含特殊角的非直角三角形】 PAGEREF _Tc29084 \h 6
\l "_Tc593" 【类型三 “独立”型】 PAGEREF _Tc593 \h 11
\l "_Tc10132" 【类型四 “背靠背”型】 PAGEREF _Tc10132 \h 14
\l "_Tc2067" 【类型五 “叠合”型】 PAGEREF _Tc2067 \h 20
\l "_Tc12911" 【类型六 “斜截”型】 PAGEREF _Tc12911 \h 24
【典型例题】
【类型一 含特殊角（“30°，45°，60°”）的非直角三角形】
例题：（2023春·江西九江·八年级校考期中）如图，A，B两地之间有一座山，汽车原来从A地到B地时需经过C地沿折线行驶，开通隧道后，汽车直接沿直线行驶．已知，，，隧道开通后，汽车从A地到B地行驶的直线距离为多少千米?

【答案】汽车从A地到B地比原来少走千米
【分析】过C作于D，在中，根据，，解直角三角形求出、的长度，然后在中，求出、的长度，用即可求解．
【详解】解：过C作于D，如图所示：

在中， ∵，，
∴，，
在中， ∵，
∴为等腰直角三角形，
∴，，
则．
答：汽车从A地到B地比原来少走．
【点睛】本题考查了解直角三角形的应用，难度适中，解答本题的关键是作三角形的高建立直角三角形幷解直角三角形．
【变式训练】
1．（2023春·江苏无锡·八年级校考阶段练习）如图，在四边形中，，，，，，则的长为 ．

【答案】
【分析】过点作，交于点，过点作，交于点，可证得四边形为矩形，根据在直角三角形中，如果一个锐角等于， 那么它所对的直角边等于斜边的一半，结合勾股定理，可求得，的长度．
【详解】如图所示，过点作，交于点，过点作，交于点，则．
∵，
∴．
∴．
∴四边形为矩形．
∴，．
∵
∴．
∴．
∴．
∴．
∵，
∴．
∴．
∴．
故答案为：10
【点睛】本题主要考查矩形的判定及性质、勾股定理，牢记矩形的判定方法和性质是解题的关键．
2．（2023秋·浙江·八年级专题练习）如图，一条船上午8时从海岛A出发，以15海里/时的速度向正北方向航行，上午10时到达海岛B处，分别从A，B处望灯塔C，测得．
(1)求海岛B到灯塔C的距离；
(2)若这条船到达海岛B处后，继续向正北方向航行，问还要经过多长时间，小船与灯塔C的距离最短？
【答案】(1)30海里
(2)1小时
【分析】（1）根据，可得等腰，再根据等腰三角形的性质即可解答；
（2）点作于点，的长度即为小船与灯塔的最短距离；然后求出的长度,最后求出时间即可解答．
【详解】（1）解：由题意得：（海里）．
∵，
∴．
∴．
∴（海里）．
∴从海岛B到灯塔C的距离为30海里．
（2）解：如图，过点C作于点P．
∴根据垂线段最短，线段的长为小船与灯塔C的最短距离，．
又∵，
∴．
在中，，
∴（海里）．
∴航行的时间为（时）．
∴这条船到达海岛B处后，继续向正北方向航行，要经过1小时，小船与灯塔C的距离最短．
【点睛】本题主要考查了等腰三角形的性质、含30°的直角三角形的性质等知识点，熟练掌握在直角三角形中所对的直角边是斜边的一半是解题的关键．
3．（2023·辽宁葫芦岛·统考二模）如图，小明在游玩时想利用手中的无人机测量一山崖（垂直于地面）的高度，小明从点看向无人机的仰角为．从无人机处测得看山崖顶端的仰角为，测得看山崖底部处的俯角为，无人机与山崖的水平距离为50米．（图中各点均在同一平面内）．

(1)求山崖的高度（结果保留根号）；
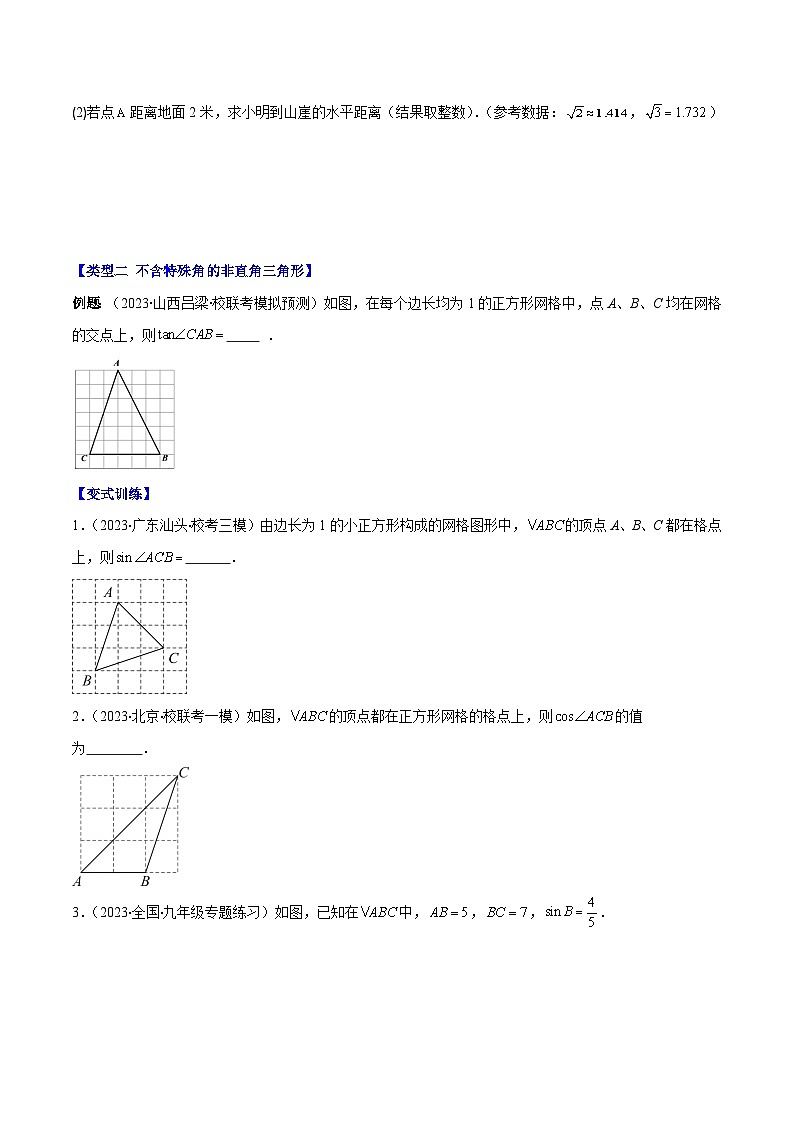
(2)若点距离地面2米，求小明到山崖的水平距离（结果取整数）．（参考数据：，）
【答案】(1)米
(2)135米
【分析】（1）利用锐角三角函数求得和，根据，即可得到答案；
（2）过点作于点，过点作于点，得矩形，进而求得，利用锐角三角函数求得，即可得到答案．
【详解】（1）解：由题意可知：，，，
在中，，
，
在中，，
，
米
答：山崖的高度约为米；
（2）解：如图，过点作于点，过点作于点，得矩形，

则，，
，
在中，，
，
，
米，
答：小明到山崖的距离约为135米．
【点睛】本题考查了解直角三角形的应用-仰俯角问题，根据题目的已知条件并结合图形添加适当辅助线是解题的关键．
【类型二 不含特殊角的非直角三角形】
例题：（2023·山西吕梁·校联考模拟预测）如图，在每个边长均为1的正方形网格中，点A、B、C均在网格的交点上，则 ．
【答案】1
【分析】取格点D，连接，根据勾股定理的逆定理得到是直角三角形，根据，得到．
【详解】解：如图所示，取格点D，连接，
∵，，，
，
∴是直角三角形，，
∵，
∴．
故答案：1．
【点睛】本题主要考查了勾股定理的逆定理，锐角三角函数等， 添加辅助线，熟练掌握勾股定理解直角三角形，勾股定理的逆定理判定直角三角形，正切的定义，是解决问题的关键．
【变式训练】
1．（2023·广东汕头·校考三模）由边长为1的小正方形构成的网格图形中，的顶点A、B、C都在格点上，则 ．

【答案】
【分析】先根据勾股定理求出，，，可知，再过点B作，然后根据勾股定理求出，即可得出答案．
【详解】根据勾股定理，得，，，
∴．
过点B作，交于点D，
∴．
在中，，
∴．
故答案为：．

【点睛】本题主要考查了锐角三角函数，勾股定理，等腰三角形的性质等，构造直角三角形是解题的关键．
2．（2023·北京·校联考一模）如图，的顶点都在正方形网格的格点上，则的值为 ．
【答案】
【分析】取格点D，连接，根据勾股定理分别求出，，，即得出，说明为直角三角形，最后根据余弦的定义求解即可．
【详解】解：如图，取格点D，连接．
∴，，，
∴，
∴为直角三角形，
∴．
故答案为：．
【点睛】本题考查勾股定理及其逆定理，余弦的定义．正确的连接辅助线是解题关键．
3．（2023·全国·九年级专题练习）如图，已知在中，，，．
(1)求；
(2)求．
【答案】(1)1
(2)
【分析】（1）过点作于点，利用，求出，利用勾股定理求出，再利用求出，进而求出；
（2）利用勾股定理求出即可．
【详解】（1）解：过点作于点，
则，
∵，
∴，
∴，
∴，
∴；
（2）解：由（1）知，在中，
．
【点睛】本题考查解直角三角形．通过作高，构造直角三角形是解题的关键．
4．（2022·湖南·统考中考真题）阅读下列材料：
在中，、、所对的边分别为、、，求证：．
证明：如图1，过点作于点，则：
在中， CD=asinB
在中，
根据上面的材料解决下列问题：
(1)如图2，在中，、、所对的边分别为、、，求证：；
(2)为了办好湖南省首届旅游发展大会，张家界市积极优化旅游环境．如图3，规划中的一片三角形区域需美化，已知，，米，求这片区域的面积．（结果保留根号．参考数据：，
【答案】(1)见解析
(2)
【分析】（1）作BC边上的高，利用三角函数表示AD后，即可建立关联并求解；
（2）作BC边上的高，利用三角函数分别求出AE和BC，即可求解．
【详解】（1）证明：如图2，过点作于点，
在中，，
在中，，
，
；
（2）解：如图3，过点作于点，
，，
，
在中，
又，
即，
，
．
【点睛】本题考查了解直角三角形的应用，掌握直角三角形的边角关系，即锐角三角函数的定义是解决问题的前提．
【类型三 “独立”型】
例题：（2023春·吉林长春·九年级校考阶段练习）如图，某校无人机兴趣小组借助无人机测量教学楼的高度，无人机在离教学楼底部处米的处垂直上升米至处，测得教学楼顶处的俯角为，则教学楼的高度约为 米．（结果精确到米）【参考数据：，，】

【答案】
【分析】过作于点，可得，根据题意可知米，米，由作图知，米，在中利用三角函数可求出的长，即可求得的长
【详解】过作于点，

，米，米，，米，
在中，，
，
米，
米，
答：教学楼的高度约为米．
【点睛】本题考查了解直角三角形的应用，借助仰角构造出直角三角形，然后利用三角函数进行求解是关键．
【变式训练】
1．（2023春·安徽淮南·九年级校联考阶段练习）如图，甲乙两楼相距30米，乙楼高度为36米，自甲楼楼顶A处看乙楼楼顶B处仰角为30°，则甲楼高度为 米；

【答案】
【分析】在中，由可求，再由，即可求解．
【详解】解：如图，

由题意得：米，米，，
在中，，
，
，
甲楼的高为（）米；
故答案：．
【点睛】本题主要考查了解直角三角形的应用，掌握解法是解题的关键．
2．（2019秋·广东佛山·九年级佛山市禅城区澜石中学校考期中）如图，小明在公园放风筝，拿风筝线的手离地面高度为，风筝飞到处时的线长为，这时测得，求此时风筝离地面的高度．（精确到，）

【答案】此时风筝离地面的高度为
【分析】根据矩形的判定和性质，直角三角形的性质，三角函数的计算方法即可求解．
【详解】解：如图所示，，，

由图可知，人垂直于地面，即垂直于地面，点到地面的高度为，即垂直于地面，且，
∴四边形是矩形，
∴，
在中，，，
∴，
∴，
∴，
∴此时风筝离地面的高度为．
【点睛】本题主要考查直角三角形的性质，矩形的判定和性质，三角函数的计算方法，掌握以上知识的运用是解题的关键．
【类型四 “背靠背”型】
例题：（2023春·山东青岛·九年级统考开学考试）科技改变生活，手机导航极大方便了人们的出行，如图，小明一家自驾到古镇C游玩，到达A地后，导航显示车辆应沿北偏西67°方向行驶4千米至B地，再沿北偏东23°方向行驶一段距离到达古镇C，小明发现古镇C恰好在A地的正北方向，求B，C两地的距离（结果保留整数）（参考数据：，，，，）．

【答案】B，C两地的距离约是10千米．
【分析】根据平行线的性质可知，推出，再根据正切的定义求出的长．
【详解】解：如图：

∵，
∴，
∴，
∴（千米）．
答：B，C两地的距离约是10千米．
【点睛】此题考查了方向角问题．此题难度适中，解此题的关键是将方向角问题转化为解直角三角形的知识，利用三角函数的知识求解．
【变式训练】
1．（2023春·江苏南通·九年级校考阶段练习）如图，一艘船由A港沿北偏东方向航行至B港，然后再沿北偏西方向航行至C港，C港在A港北偏东方向，则A，C两港之间的距离为 ．

【答案】
【分析】根据题意得，，，，过B作于E，解直角三角形即可得到结论．
【详解】解：根据题意得，，，，过B作于E，

∴，
在中，
∵，，
∴，
在中，
∵，
∴，
∴，
∴，
∴A，C两港之间的距离为，
故答案为：．
【点睛】本题考查了解直角三角形的应用-方向角问题，正确作出辅助线构造直角三角形是解答本题的关键．
2．（2023春·海南省直辖县级单位·九年级统考期中）某校举办以“测量”为主题的数学实践活动，该校数学兴趣小组准备借助无人机来测量小区内的一座大楼高度．如图所示，无人机从地面点A处沿着与地面垂直的方向上升，至点B处时，测得大楼底部C的俯角为30°，E测得大楼顶部D的仰角为45°．无人机保持航向不变继续上升50米到达点E处，此时测得大楼顶部D的俯角为60°．已知A、C两点在同一水平线上．

(1)填空：＝_________度，＝_________度；
(2)求A、C两点间的距离：（结果保留根号）
(3)求这座大楼的高度．（结果保留根号）
【答案】(1)；
(2)米
(3)米
【分析】（1）根据俯角和仰角的定义求解即可；
（2）设，在中可得，在中可得，在中可得，最后由列方程求解即可；
（3）由求解即可．
【详解】（1）如图，

由题意可得，，，，，，，
∴,，
故答案为：；；
（2）设，则，
在中可得，
在中可得，
在中可得，
∴
解得：，
∴；
（3）由（2）可得，，
∴
【点睛】本题考查解直角三角形-仰角俯角问题，解题的关键是作辅助线，构造直角三角形解决问题．
3．（2023·黑龙江大庆·统考一模）如图，某无人机兴趣小组在操场上展开活动，此时无人机在离地面30米的D处，无人机测得操控者A的俯角为，测得教学楼顶端点C处的俯角为，又经过人工测量测得操控者A和教学楼之间的距离为57米．（点A，B，C，D都在同一平面上，结果保留根号）

(1)填空： ______度， ______度；
(2)求此时无人机与教学楼之间的水平距离的距离；
(3)求教学楼的高度．
【答案】(1)105，135
(2)无人机与教学楼BC之间的水平距离BE的距离为米
(3)教学楼BC的高度为米
【分析】（1）延长交于点，根据题意可得，，，则，再根据三角形的外角定理求出即可；
（2）过点A作，垂足为F．根据题意可得，米，米，则，再根据即可求解；
（3）在中，，则，即可求解．
【详解】（1）解：如图：延长交于点，

由题意得：，，，
∴，
∵是的一个外角，
∴，
故答案为：105，135；
（2）解：过点A作，垂足为F．

由题意得：，米，米，
在中，，
（米），
∴米，
∴米，
∴此时无人机与教学楼之间的水平距离BE的距离为米；
（3）解：在中，，米，
∴米，
∴米，
∴教学楼的高度为米．
【点睛】本题主要考查了解直角三角形的实际应用，解题的关键是正确画出辅助线，构造直角三角形，熟练掌握解直角三角形的方法和步骤．
【类型五 “叠合”型】
例题：（2023春·河南驻马店·九年级统考阶段练习）文峰塔位于河南省安阳市古城内西北隅，因塔建于天宁寺内，又名天宁寺塔；文峰塔建于五代后周广顺二年，已有一千余年历史，风格独特，具有上大下小的特点．由下往上一层大于一层，逐渐宽敞，是伞状形式，这种平台、莲座、辽式塔身、藏式塔刹的形制世所罕见．
活动课上，数学社团的学生计划测量文峰塔的高度．如图所示，先在点C处用高1.6m的测角仪测得塔尖A的仰角为37°，向塔的方向前进12m到达F处，在F处测得塔尖A的仰角为45°，请你相关数据求出文峰塔的高度．（结果精确到1m，参考数据：，，，．）

【答案】文峰塔的高度约为38米
【分析】延长交于点G，设米，在中，求出的长，进而得出的长，中，利用，进行求解即可．
【详解】解：延长交于点G．

由题意得：米，米，．
设米．在中，，
∴（米）．
∴米．
在中，，
∴，解得．
经检验：是原方程的根．
∴（米）．
答：文峰塔的高度约为38米．
【点睛】本题考查解直角三角形的应用，解题的关键是构造直角三角形，熟记锐角三角函数的定义．
【变式训练】
1．（2023春·湖南株洲·九年级统考期中）小军和小明在同一个班，他们都是数学爱好者，并且住在同一个小区的A栋楼，学完解直角三角形后，他们决定用所学知识来求距离，如图：A、B两栋楼，他们站在自家阳台上测得对面B栋楼的楼顶P点的仰角分别为．已知小军家与小明家阳台垂直距离为30米．
（参考数据：）

(1)求A、B两栋楼的楼间距为多少米？（结果精确到米）
(2)已知小明家阳台与地面的垂直距离为6米，求对面B栋楼的高度．（结果精确到米）
【答案】(1)A、B两栋楼的楼间距约为米；
(2)对面B栋楼的高度约为米．
【分析】（1）过点P作，交的延长线于点E，根据题意得，，根据三角形的外角性质得，从而可得米，然后在中，利用锐角三角函数的定义求出的长，即可解答；
（2）根据题意可得：米，米，，然后在中，利用锐角三角函数的定义求出的长，从而利用线段的和差关系，进行计算即可解答．
【详解】（1）解：过点P作，交的延长线于点E，

由题意得：，，
∵是的一个外角，
∴，
∴，
∴米，
在中，（米），
∴米，
∴A、B两栋楼的楼间距约为米；
（2）解：如图：

由题意得：米，米，，
在中，，
∴（米），
∴（米），
∴对面B栋楼的高度约为米．
【点睛】本题考查了解直角三角形的应用-仰角俯角问题，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
2．（2023·江苏苏州·校考二模）如图，某中学数学课题学习小组在“测量物体高度”的活动中，欲测量一棵古树的高度，他们在这棵古树的正前方一平房顶点处测得古树顶端的仰角为，在这棵古树的正前方处，测得古树顶端的仰角为，在点处测得点的俯角为，已知为米，且、、三点在同一条直线上．

(1)求平房的高度；
(2)请求出古树的高度．（根据以上条件求解时测角器的高度忽略不计）
【答案】(1)
(2)
【分析】（）在中，已知 ， ，利用角的正切可得出结果
（）在中，由正切函数的定义求出的长，最后解，即可求出的长，即古树的高度．
【详解】（1）由题意知，，
，
（2），，
∴，
，，，
，，
，
在中，．
【点睛】本题考查的是解直角三角形的应用仰角、俯角问题，熟记锐角三角函数的定义是解答此题的关键．
【类型六 “斜截”型】
例题：（2023春·辽宁阜新·九年级校考阶段练习）如图，在南北方向的海岸线上，有A，B两艘巡逻船，现均收到故障船C的求救信号，已知A，B两船相距海里，船C在船A的北偏东方向上，船C在船B的东南方向上，上有一观测点D，测得船C正好在观测点D的南偏东方向上．

(1)求出A与C之间的距离．
(2)已知距观测点D处100海里范围内有暗礁．若巡逻船A沿直线去营救船C，在去营救的途中有无触暗礁危险？（参考数据：，）
【答案】(1)200海里
(2)无触暗礁危险
【分析】（1）作于点E，设海里，则海里，根据可列出方程求得的值后即可求得的长；
（2）根据（1）中结论得出的长，再与100比较即可得到答案．
【详解】（1）解：作于点E，

由题意得：，，
设海里，
在中，，
在中，，
，
解得：，
，
与C之间的距离等于（海里）；
（2）解：由（1）知，（海里），
，
所以巡逻船A沿直线去营救船C，在去营救的途中无触暗礁危险．
【点睛】本题考查的是解直角三角形的应用—方向角问题，根据题意作出辅助线，构造出直角三角形是解题关键．
【变式训练】
1．（2023·内蒙古·统考中考真题）某数学兴趣小组借助无人机测量一条河流的宽度．如图所示，一架水平飞行的无人机在处测得河流左岸处的俯角为，无人机沿水平线方向继续飞行12米至处，测得河流右岸处的俯角为，线段米为无人机距地面的铅直高度，点，，在同一条直线上，其中．求河流的宽度（结果精确到1米，参考数据：）．
【答案】河流的宽度约为64米
【分析】过点作于点，分别解、即可．
【详解】解：过点作于点．则四边形是矩形．
∴，
∵
∴
在中，
∴，
∴
∴
在中，，
∴，∴
，
∴
∴米
答：河流的宽度约为64米．
【点睛】本题考查了关于俯仰角的解直角三角形的问题．作垂线构造直角三角形是解题关键．
2．（2023·江苏盐城·校考二模）如图，是某景区一段坡度的上坡路段，为竖直（与水平面垂直）的监控立杆，点D处安装了摄像头，点A、B分别为摄像头的测速起点与终点．安装调试摄像头时，在摄像头D处测得点A的俯角为，点B的俯角为．已知米，点O、A、B、C、D、E、在同一平面内．

(1)求杆的高度；（精确到个位）
(2)一辆小汽车从A点驶向B点，摄像头两次测速抓拍的时间间隔为秒．若，此路段的限速是40千米/小时，试判断这辆小汽车是否超速违章，并说明理由．（参考数据：，，，）
【答案】(1)杆的高度约为9米；
(2)小汽车没有超速违章，理由见解析
【分析】（1）过点D作，过点B作交的延长线于点M，设为x，则为7x，由勾股定理求得米，米，进而得到为9米；
（2）过点C作于点N，由推导出，进而得到米，米，米，推导出小汽车的速度为千米/小时，进而得出结论．
【详解】（1）解：如图，过点D作，过点B作交的延长线于点M，

∵是坡度的公路，
∴设为x米，则为7x米，
由勾股定理得：，
∵米，
∴，
∴，即（米），
∵，
∴（米），
∴（米），
答：杆的高度约为9米；
（2）小汽车没有超速违章．理由如下： 如图，过点C作于点N，

由题可知，，
∵，
∴，
由（1）得米，
∴（米），
∵，
∴（米），
∴（米），
∴此时小汽车的速度为（米/秒）（千米/小时），
∵，
∴小汽车没有超速违章．
【点睛】本题考查了解直角三角形的应用，作出合适的辅助线构建直角三角形，熟练掌握锐角三角函数的正弦，余弦，正切是解题的关键．