宁夏石嘴山市第三中学2022-2023学年高一上学期期中数学试题（Word版附解析）

这是一份宁夏石嘴山市第三中学2022-2023学年高一上学期期中数学试题（Word版附解析），共16页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1. 设集合，，则（ ）
A. B. C. D.
【答案】A
【解析】
【分析】利用并集的定义直接求解．
【详解】解：∵集合，，
∴．
故选：A．
2. 若函数是函数（且）的反函数，且，则（ ）
A. B. C. D.
【答案】B
【解析】
分析】
由题意可得出，结合可得出的值，进而可求得函数的解析式.
【详解】由于函数是函数（且）的反函数，则，
则，解得，因此，.
故选：B.
3. 若函数的一个零点（正数）附近的函数值用二分法逐次计算，参考数据如下表：那么方程的一个近似解（精确度0.04）为（ ）
A. 1.5B. 1.25C. 1.375D. 1.4375
【答案】D
【解析】
【分析】根据零点存在定理判断求解．
【详解】由表格结合零点存在定理知零点在上，区间长度为0.03125，满足精度要求，观察各选项，只有D中值1.4375是该区间的一个端点，可以作为近似解，
故选：D．
4. 函数的零点所在区间为（ ）
A. B. C. D.
【答案】A
【解析】
【分析】判断出所给区间的端点值的乘积小于0可得答案.
【详解】；；
；；；
所以.
故选：A.
5. 已知，则（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据指对数函数的单调性即可判断a、b、c的大小.
【详解】由，
∴.
故选：B.
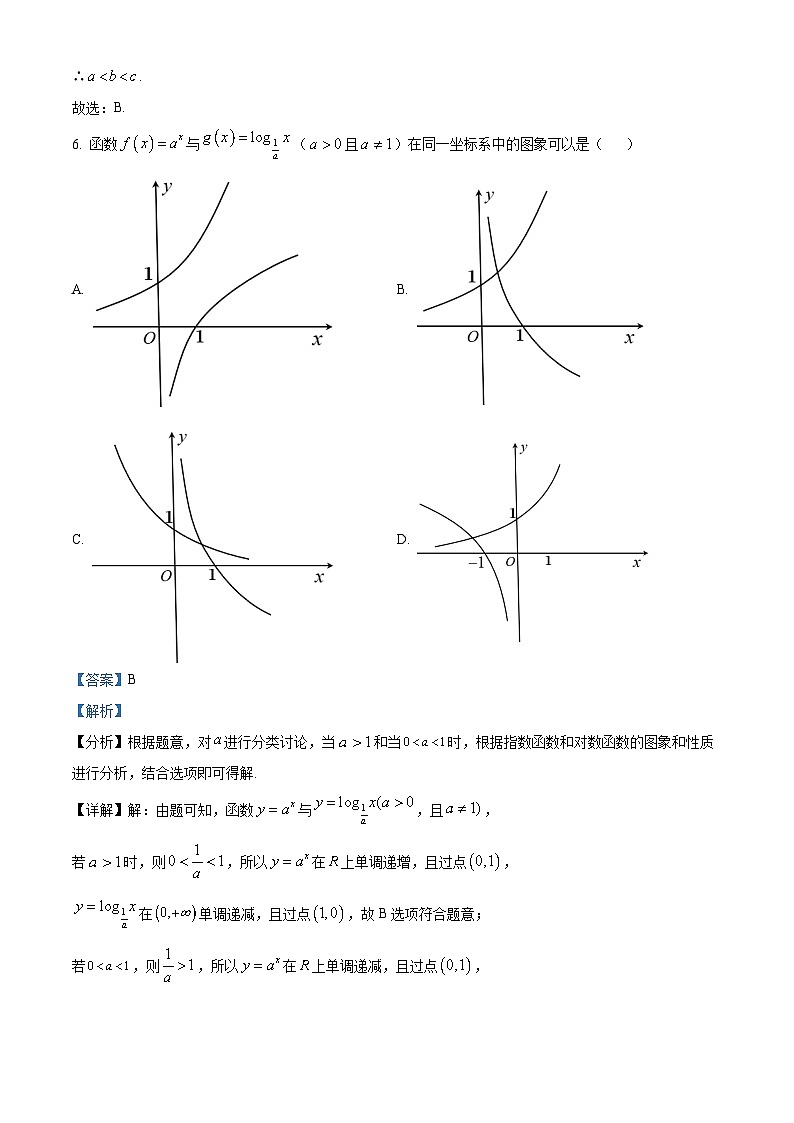
6. 函数与（且）在同一坐标系中的图象可以是（ ）
A. B.
C. D.
【答案】B
【解析】
【分析】根据题意，对进行分类讨论，当和当时，根据指数函数和对数函数的图象和性质进行分析，结合选项即可得解.
【详解】解：由题可知，函数与，且，
若时，则，所以在上单调递增，且过点，
在单调递减，且过点，故B选项符合题意；
若，则，所以在上单调递减，且过点，
在单调递增，且过点，没有符合题意的选项.
故选：B.
7. 已知函数（且），是R上的减函数，则实数a的取值范围为（ ）
A B. C. D.
【答案】C
【解析】
【分析】根据分段函数的单调性即可求解.
【详解】解：因为（且），是R上的减函数
所以满足：
解得：
所以实数a的取值范围为：
故选：C.
8. 已知函数，若，，均不相等，且= =，则的取值范围是（ ）
A. （1，10）B. (5，6)C. (10，12)D. (20，24)
【答案】C
【解析】
【分析】画出函数图象，根据，不妨设，结合图象可求出范围
【详解】函数的图象如图所示，
不妨设，则，
所以，，
所以，，
所以，
故选：C
二、多项选择题：本属共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，有选错的得0分，部分选对的得2分．
9. 下列各图中，是函数图象的是（ ）
A. B.
C. D.
【答案】BD
【解析】
【分析】根据函数的定义，进行分析判断即可得解.
【详解】根据函数的定义可知，定义域内的每一个只有一个和它对应，
满足条件的只有BD.
故选：BD
10. 已知函数是一次函数，满足，则的解析式可能为（ ）
A. B.
C. D.
【答案】AD
【解析】
【分析】
设，表示出，根据对应系数相等求解和的值.
【详解】设，则，则，所以，得或，所以或.
故选：AD.
11. 下列说法正确的是（ ）
A. 若的定义域为，则的定义域为
B. 函数的值域为
C. 函数的值域为
D. 函数在上的值域为
【答案】AC
【解析】
【分析】根据抽象函数的定义域的求解判断A；利用分离常数化简函数解析式，结合反比型函数的值域判断B；利用换元法，结合二次函数的性质求得其值域，判断C；利用配方法，结合二次函数的性质判断D.
【详解】对于A，因为的定义域为，所以，
解得，即的定义域为，故A正确；
对于B，，
所以，即函数的值域为，故B不正确；
对于C，令，则，，
所以，，
所以当时，该函数取得最大值，最大值为，
所以函数的值域为，故C正确；
对于D，，其图象的对称轴为直线，且，，
所以函数在上的值域为，故D不正确．
故选：AC．
12. 某医药研究机构开发了一种新药，据监测，如果患者每次按规定的剂量注射该药物，注射后每毫升血液中的含药量y（微克）与时间t（小时）之间的关系近似满足如图所示的曲线．据进一步测定，当每毫升血液中含药量不少于0.125微克时，治疗该病有效，则（ ）
A.
B. 注射一次治疗该病的有效时间长度为6小时
C. 注射该药物小时后每毫升血液中的含药量为0.4微克
D. 注射一次治疗该病的有效时间长度为时
【答案】AD
【解析】
【分析】利用图象分别求出两段函数解析式，再进行逐个分析，即可解决．
【详解】由函数图象可知，
当时，，即，解得，
，故正确，
药物刚好起效的时间，当，即，
药物刚好失效的时间，解得，
故药物有效时长为小时，
药物的有效时间不到6个小时，故错误，正确；
注射该药物小时后每毫升血液含药量为微克，故错误，
故选：．
三、填空题：本大题共4小题，每小题5分，满分20分．
13. 已知幂函数的图象经过点，则的值为__________.
【答案】
【解析】
【分析】
设幂函数的解析式为，代入点，求得，即可求解的值，得到答案.
【详解】设幂函数的解析式为，
因为幂函数的图象经过点，
可得，解得，即，
所以.
故答案：.
14. 若，则实数a的取值范围是_______．
【答案】（0，）∪（1，＋∞）
【解析】
【分析】对分类讨论，再解不等式即得解.
【详解】当时，不等式为.
当时，不等式为.
综上所述，实数a的取值范围是（0，）∪（1，＋∞）
故答案为（0，）∪（1，＋∞）
【点睛】本题主要考查对数函数的图像和性质，意在考查学生对这些知识的理解掌握水平和分析推理能力.
15. 关于的不等式的解集为，且，则实数______．
【答案】##
【解析】
【分析】根据一元二次不等式与对应一元二次方程的关系求解即可.
【详解】由题意，的两根为，
所以，
解得，或，
当时，故，
由知，所以解得，
当时，不合题意.
故答案为：
16. 给出下列结论：
①；
②，，的值域是；
③幂函数图像一定不过第四象限；
④函数的图像过定点；
⑤若成立，则的取值范围是，其中正确的序号是___________.
【答案】③④
【解析】
【分析】①偶次开根，结果非负；
②二次函数值域，数形结合求解；
③幂函数自变量为正时，指数幂的底数为正，函数值为正，即图像在第一象限，不过第四象限；
④指数型函数过定点，令的指数部分f(x)＝0；
⑤对数的真数部分大于零﹒
【详解】①2，因此①不正确；
②y＝x2+1，x∈[﹣1，2]，y的值域是[1，5]，因此②不正确；
③幂函数自变量为正时，指数幂的底数为正，函数值为正，即图像在第一象限，不过第四象限，因此③正确；
④当x＝﹣1时，f（﹣1）＝a0﹣2＝﹣1，∴函数f（x）＝ax+1﹣2（a＞0，a≠1）的图象过定点（﹣1，﹣1），因此④正确；
⑤若lna＜1成立，则a的取值范围是（0，e），因此⑤不正确．
故答案为：③④．
四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．
17. 计算：
（1）；
（2）
【答案】（1）4； （2）.
【解析】
【分析】（1）应用有理指数幂的运算性质化简求值即可.
（2）应用对数的运算性质化简求值即可.
【小问1详解】
原式=.
【小问2详解】
原式=.
18. 已知函数，且.
（1）求的解析式；
（2）用单调性的定义证明函数在其定义域上为增函数；
（3）解关于的不等式 .
【答案】（1）
（2）证明见解析 （3）
【解析】
【分析】(1)由题意结合函数的解析式可求得m=1，则可确定函数的解析式；(2)根据单调性的定义证明；(3)由题意结合函数的单调性，得到关于实数x的不等式组，运算求解.
【小问1详解】
由题意：，即.
∴的解析式.
【小问2详解】
对任意，令，则有：
，
∵
∴，即
故在定义域(0,+∞)上为增函数；
【小问3详解】
由(2)可知在定义域(0,+∞)上为增函数
则原不等式等价于，即，
则可得：，解得：.
故不等式的解集为.
19. 已知函数，其中.且.
（1）求函数的定义域；
（2）判断的奇偶性，并说明理由；
（3）若，求使成立的的集合.
【答案】（1）
（2）奇函数，理由见解析
（3）
【解析】
【分析】（1）根据对数函数的定义求函数的定义域；
（2）由奇偶性性定义判断；
（3）由函数值求得值，然后根据对数函数的性质解不等式．
【小问1详解】
要使函数有意义，则，
解得，
即函数的定义域为；
【小问2详解】
，
是奇函数.
【小问3详解】
若，
解得：，
若，则，
，解得，
故不等式的解集为.
20. 今年的新冠肺炎疫情是21世纪以来规模最大的突发公共卫生事件，疫情早期，武汉成为疫情重灾区，据了解，为了最大限度保障人民群众的生命安全，现需要按照要求建造隔离病房和药物仓库.已知建造隔离病房的所有费用（万元）和病房与药物仓库的距离（千米）的关系为：.若距离为1千米时，隔离病房建造费用为100万元.为了方便，隔离病房与药物仓库之间还需修建一条道路，已知购置修路设备需5万元，铺设路面每公里成本为6万元，设为建造病房与修路费用之和.
（1）求的表达式；
（2）当隔离病房与药物仓库距离多远时，可使得总费用最小？并求出最小值
【答案】（1）；
（2）当时，费用取得最小，最小值为75万元.
【解析】
【分析】(1)根据距离为1km时隔离病房建造费用为100万元，求出k的值，由此可得的表达式；
(2)由(1)可得，利用基本不等式计算即可求解.
【小问1详解】
由题意知，距离为1km时，隔离病房建造费用为100万元，
所以，得，
所以；
【小问2详解】
由(1)知，
，
当且仅当即时，等号成立，
即当时，函数取到最小值75万元，
所以隔离病房与药物仓库距离5km时，可使得总费用最小，最小值为75万元.
21. 已知函数（）．
（1）若函数在上是减函数，求的取值范围；
（2）当时，设函数的最小值为，最大值为，求函数与的表达式．
【答案】（1）
（2）；
【解析】
【分析】（1）根据单调区间与对称轴的关系求解；
（2）分对称轴与区间的关系求函数最小值，根据对称轴与0的大小关系分类求最大值即可.
【小问1详解】
因为函数在上是减函数，且其对称轴为，
所以．
【小问2详解】
①当时，函数单调递增，；
②当时，函数先减后增；
③当时，函数单调递减．
故；
当时，；当时，
故
22. 设函数且是定义域为R的奇函数．
求k值；
若，试判断函数单调性并求使不等式恒成立的t的取值范围；
若，且在上最小值为，求m的值．
【答案】（1）2；（2）；（3）2
【解析】
【详解】试题分析：（1）根据奇函数的性质可得f（0）=0，由此求得k值；（2）由（a＞0且a≠1），f（1）＜0，求得1＞a＞0，f（x）在R上单调递减，不等式化为，即恒成立，由△＜0求得t的取值范围；（3）由求得a的值，可得 g（x）的解析式，令，可知为增函数，t≥f（1），令，分类讨论求出h（t）的最小值，再由最小值等于2，求得m的值
试题解析：（1）∵f（x）是定义域为R的奇函数，∴f（0）＝0，∴1－（k－1）＝0，
∴k＝2，
（2）
单调递减，单调递增，故f（x）在R上单调递减．
不等式化为
，
解得
（3）
，
由（1）可知为增函数,
令h（t）＝t2－2mt＋2＝（t－m）2＋2－m2（t≥）
若m≥，当t＝m时，h（t）min＝2－m2＝－2，∴m＝2
若m<，当t＝时，h（t）min＝－3m＝－2，解得m＝>，舍去
综上可知m＝2．
考点：1．指数函数综合题；2．函数奇偶性的性质