数学北师大版4 数据的离散程度教学ppt课件

这是一份数学北师大版4 数据的离散程度教学ppt课件，共22页。PPT课件主要包含了学习目标，复习导入，探究新知，甲的平均成绩比乙好，典例精讲，课堂练习，课堂小结等内容，欢迎下载使用。

1．通过更为丰富的例子，让学生较为全面地理解方差及其在现实生活中的应用。2．通过实例，让学生体会数据的离散程度在现实生活中广泛存在，应视情况分析方差或标准差对于问题的影响。
回顾：什么是极差、方差、标准差？方差的计算公式是什么？一组数据的方差与这组数据的波动有怎样的关系？
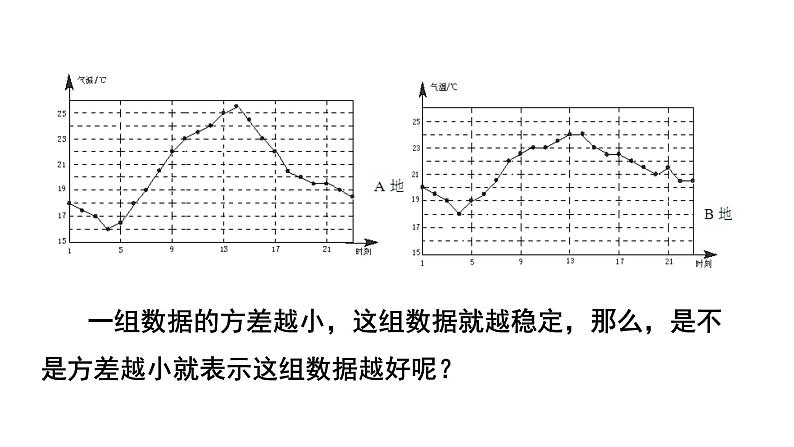
试一试：如图是某一天A、B两地的气温变化图，请回答下列问题：（1）不进行计算，说说A、B两地这一天气候的特点（2）分别计算这一天A、B两地气温的平均数和方差，与你刚才的看法一致吗？
A、B两地平均气温相近，但A地日温差较大，B地日温差较小．
A地平均气温20.42 ℃，方差7.76； B地平均气温21.35 ℃，方差2.78．
一组数据的方差越小，这组数据就越稳定，那么，是不是方差越小就表示这组数据越好呢？
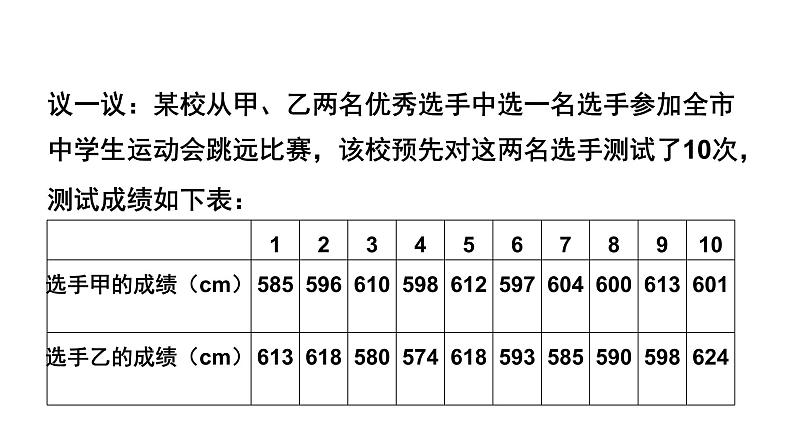
议一议：某校从甲、乙两名优秀选手中选一名选手参加全市中学生运动会跳远比赛，该校预先对这两名选手测试了10次，测试成绩如下表：
（1）他们的平均成绩分别是多少？（2）甲、乙这10次比赛成绩的方差分别是多少？（3）这两名运动员的运动成绩各有什么特点？
甲601.6 cm，乙599.3 cm。
甲65.84，乙284.21.
甲运动员成绩较稳定，因为极差、方差都比较小
乙较有潜质，因为乙的最远成绩比甲的最远成绩好
（4）历届比赛表明，成绩达到596cm就很可能夺冠，你认为为了夺冠应选谁参加这项比赛？（5）如果历届比赛表明，成绩达到610cm就能打破记录，你认为为了打破记录应选谁参加这项比赛？
在10次比赛中，甲运动员有9次超过596cm，而乙仅有5次，因此一般应选甲运动员参加这项比赛。
若要打破610cm的跳远记录，则一般应选乙运动员。
（1）两人一组，在安静的环境中，一人估计1分钟的时间，另一人记下实际时间，将结果记录下来．（2）在吵闹的环境中，再做一次这样的试验．（3）将全班的结果汇总起来，并分别计算安静状态和吵闹环境中估计结果的平均值和方差．（4）两种情况下的结果是否一致？说明理由．
　　某校从甲乙两名优秀选手中选一名选手参加全市中学生田径百米比赛（100米记录为12.2秒，通常情况下成绩为12.5秒可获冠军）．该校预先对这两名选手测试了8次，测试成绩如下表：　　根据测试成绩，请你运用所学过的统计知识做出判断，派哪一位选手参加比赛更好？为什么？
　　解：通过计算，得 S甲2=0.0775，S乙2=0.2525，　　推荐甲参加全市比赛更合适，理由如下：两人的平均成绩相等，说明实力相当；但甲的8次测试成绩的方差比乙小，说明甲发挥较为稳定，故推荐甲参加比赛更合适．
　　1．甲、乙两学生在一年里，学科平均分相等，但它们的方差不相等，正确评价他们的学习情况是（ 　 ）　　A．因为他们平均分相等，所以学习水平一样　　B．成绩虽然一样，方差较大的，说明潜力大，学习态度踏实　　C．表面上看这两个学生平均成绩一样，但方差小的学习成绩较稳定　　D．平均分相等，方差不等，说明学习水平不一样，方差较小的同学学习较稳定
2．甲、乙、丙三名射击运动员在某场测试中各射击20次，3人的测试成绩如下表
则甲、乙、丙3名运动员测试成绩最稳定的是（ ） A．甲 B．乙 C．丙 D．3人成绩稳定情况相同 3．甲、乙两人各射击6次，甲所中的环数是8，5，5，a，b，c，且甲所中的环数的平均数是6，众数是8；乙所中的环数的平均数是6，方差是4．根据以上数据，对甲、乙射击成绩的稳定的是 ．
5．水稻种植是嘉兴的传统农业．为了比较甲、乙两种水稻的长势，农技人员从两块试验田中，分别随机抽取5棵植株，将测得的苗高数据绘制成下图：
请你根据统计图所提供的数据，计算平均数和方差，并比较两种水稻的长势．
6．为了比较市场上甲、乙两种电子钟每日走时误差的情况，从这两种电子钟里，各随机抽取10台进行测试，两种电子钟每天走时误差的数据如下表（单位：s）：
（1）计算甲、乙两种电子钟走时误差的平均数；（2）计算甲、乙两种电子钟走时误差的方差；（3）根据经验，走时稳定性较好的的电子钟质量更优．若两种类型的电子钟价格相同，则你买哪种电子钟？为什么？
在本节课的学习中，你对方差的大小有什么新的认识？新认识：方差越小表示这组数据越稳定，但不是方差越小就表示这组数据越好，而是对具体的情况进行具体分析才能得出正确的结论．