初中数学人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.1 二次函数巩固练习

这是一份初中数学人教版九年级上册第二十二章 二次函数22.1 二次函数的图象和性质22.1.1 二次函数巩固练习，共38页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
一、单选题
1．如图，直线yx+3分别与x轴，y轴交于点A、点B，抛物线y=x2+2x﹣2与y轴交于点C，点E在抛物线y=x2+2x﹣2的对称轴上移动，点F在直线AB上移动，CE+EF的最小值是（ ）
A．4B．4.6C．5.2D．5.6
2．已知抛物线具有如下性质：抛物线上任意一点到定点F（0，2）的距离与到x轴的距离相等，点M的坐标为（3，6），P是抛物线上一动点，则△PMF周长的最小值是（ ）
A．5B．9C．11D．13
3．如图，在抛物线上有，两点，其横坐标分别为1，2；在轴上有一动点，当最小时，则点的坐标是（ ）
A．（0.0）B．（0，）C．（0，2）D．（0，）
4．如图，抛物线y＝﹣x2+2x+2交y轴于点A，与x轴的一个交点在2和3之间，顶点为B．下列说法：其中正确判断的序号是（ ）
①抛物线与直线y＝3有且只有一个交点；
②若点M（﹣2,y1），N（1,y2），P（2,y3）在该函数图象上，则y1＜y2＜y3；
③将该抛物线先向左，再向下均平移2个单位，所得抛物线解析式为y＝（x+1）2+1；
④在x轴上找一点D，使AD+BD的和最小，则最小值为．
A．①②④B．①②③C．①③④D．②③④
5．如图，在平面直角坐标系中，已知抛物线的对称轴为，且经过点A（2，1），点是抛物线上的动点，的横坐标为，过点作轴，垂足为，交于点，点关于直线的对称点为，连接，，过点A作AE⊥x轴，垂足为E，则当（ ）时，的周长最小.
A．1B．1.5C．2D．2.5
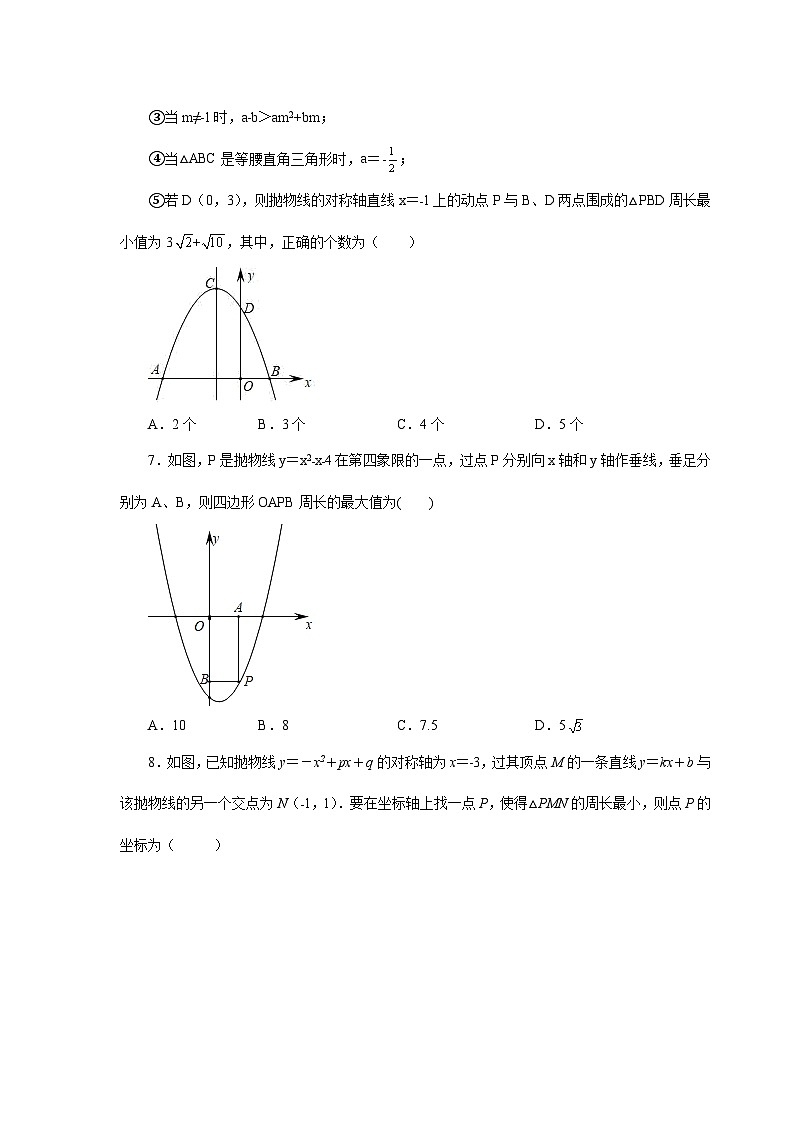
6．如图，抛物线y＝ax2+bx+c交x轴分别于点A（﹣3，0），B（1，0），交y轴正半轴于点D，抛物线顶点为C．下列结论
①2a﹣b＝0；
②a+b+c＝0；
③当m≠﹣1时，a﹣b＞am2+bm；
④当△ABC是等腰直角三角形时，a＝；
⑤若D（0，3），则抛物线的对称轴直线x＝﹣1上的动点P与B、D两点围成的△PBD周长最小值为3，其中，正确的个数为（ ）
A．2个B．3个C．4个D．5个
7．如图，P是抛物线y＝x2﹣x﹣4在第四象限的一点，过点P分别向x轴和y轴作垂线，垂足分别为A、B，则四边形OAPB周长的最大值为( )
A．10B．8C．7.5D．5
8．如图，已知抛物线y＝－x2＋px＋q的对称轴为x＝﹣3，过其顶点M的一条直线y＝kx＋b与该抛物线的另一个交点为N（﹣1，1）．要在坐标轴上找一点P，使得△PMN的周长最小，则点P的坐标为（ ）
A．（0，2）B．（，0）
C．（0，2）或（，0）D．以上都不正确
9．抛物线与直线交于A、B两点（点A在点B的左侧），动点P从A点出发，先到达抛物线的对称轴上的某点E，再到达x轴上的某点F，最后运动到点B．若使点P运动的总路径最短，则点P运动的总路径的长为（ ）
A．B．C．D．
二、填空题
10．如图，抛物线与x轴分别交于A、B两点（点A在点B的左侧），与y轴交于C，在其对称轴上有一动点M，连接MA、MC、AC，则当△MAC的周长最小时，点M的坐标是_____．
11．若抛物线y＝﹣x2+2x+m+1（m为常数）交y轴于点A，与x轴的一个交点在2和3之间，抛物线顶点为点B．
①抛物线y＝﹣x2+2x+m+1与直线y＝m+2有且只有一个交点；
②若点M（﹣2，y1）、点N（，y2）、点P（2，y3）在该函数图象上，则y1＜y2＜y3；
③将该抛物线向左平移2个单位，再向下平移2个单位，所得的抛物线解析式为y＝﹣（x+1）2+m；
④点A关于直线x＝1的对称点为C，点D、E分别在x轴和y轴上，当m＝1时，四边形BCDE周长的最小值为．
其中正确的是 ___．（填序号）
12．如图，在平面直角坐标系中，点A在抛物线y＝x2﹣2x＋2上运动．过点A作AC⊥x轴于点C，以AC为对角线作矩形ABCD，连接BD，则对角线BD的最小值为_____．
13．如图，抛物线与x轴交于A，B两点（点A在B的左侧），点C为抛物线上任意一点（不与A，B重合），为的边上的高线，抛物线顶点与点的最小距离为1，则抛物线解析式为______．
14．如图，在平面直角坐标系中，直线AC：y＝x+8与x轴交于点A，与y轴交于点C，抛物线y＝ax2+bx+c过点A，C，且与x轴的另一交点为B，又点P是抛物线的对称轴l上一动点．若△PAC周长的最小值为10+2，则抛物线的解析式为_____．
15．如图，抛物线y＝﹣x2+x+3与x轴交于点A，B（点A在点B的左边），交y轴于点C，点P为抛物线对称轴上一点．则△APC的周长最小值是_____．
16．已知抛物线yx22x3与x轴交于A、B两点，与y轴交于点C，P是抛物线对称轴l上的一个动点，则PAPC的最小值是__________．
17．已知二次函数y=x2+bx的图象过点A(4，0)，设点C(1，-3)，在抛物线的对称轴上求一点P，使|PA-PC|的值最大，则点P的坐标为____________。
18．点是抛物线的图象上一点，过向轴作垂线，垂足为点，当点在第一象限抛物线上运动的过程中，的值最大时，点的坐标________．
19．如图，抛物线y＝﹣x2+2x+3交x轴于A，B两点，交y轴于点C，点D为抛物线的顶点，点C关于抛物线的对称轴的对称点为E，点G，F分别在x轴和y轴上，则四边形EDFG周长的最小值为_____．
20．已知二次函数y=-x2-2x+3的图象与x轴分别交于A、B两点（如图所示），与y轴交于点C，点P是其对称轴上一动点，当PB+PC取得最小值时，点P的坐标为__________．
21．如图，已知点A（1，1）、B（3，2），且P为x轴上一动点，则△ABP的周长的最小值为_______．
三、解答题
22．如图，抛物线经过点，与轴交于点过点且平行于轴的直线交抛物线于点．
（1）求抛物线的解析式；
（2）求的面积；
（3）在该抛物线的对称轴上是否存在点，使得的周长最小？若存在，求出点的坐标；若不存在，请说明理由．
23．如图，抛物线y＝x2+x﹣2与x轴交于A、B两点，与y轴交于点C．
（1）求点A，点B和点C的坐标；
（2）抛物线的对称轴上有一动点P，求PB+PC的值最小时的点P的坐标．
24．如图，二次函数y=-x2+2x+3的图象过点A(−1，0)、点B(0，3)．
（1）该二次函数的顶点是 ；
（2）点C为点B关于抛物线对称轴的对称点，直线y=mx+n经过A、C两点，满足ax2+bx+c>mx+n的x的取值范围是 ．
（3）在对称轴上找一点M，使取得最大值，求出此时M的坐标．
25．如图，已知抛物线y＝ax2+bx+3经过A（﹣3，0），B（1，0）两点，其顶点为D，对称轴是直线l，l与x轴交于点H．
（1）求该抛物线的解析式；
（2）若点P是该抛物线对称轴l上的一个动点，求△PBC周长的最小值．
26．如图，抛物线y＝x2－2x－3与x轴交于A、B两点，与y轴交于点C，点P是抛物线对称轴上的一个动点，如果△PAC的周长最小，求点P的坐标．
27．如图，抛物线与直线分别相交于、两点，其中点在轴上，且此抛物线与轴的一个交点为．
（1）求抛物线的解析式
（2）在抛物线对称轴上找一点，使的周长最小，请求出这个周长的最小值．
参考答案
1．C
【分析】
C点关于对称轴对称的点C'，过点C'作直线AB的垂线，交对称轴与点E，交直线AB于点F，则C'F即为所求最短距离．
解：∵y=x2+2x﹣2的对称轴为，C(0，﹣2)，
∴C点关于对称轴对称的点C'(﹣2，﹣2)，
过点C'作直线AB的垂线，交对称轴与点E，交直线AB于点F，
∴CE=C'E，
则C'F=CE+EF=C'E+EF是CE+EF的最小值；
∵直线yx+3，
设直线C'F的解析式为，
将C'(﹣2，﹣2)代入得：，
解得：，
∴C'F的解析式为yx，
解方程组，
得：，
∴F(，)，
∴C'F．
故选：C．
【点拨】本题考查二次函数与一次函数的图象及性质；利用点的对称性，点到直线的垂线段最短，确定最短距离为线段C'F的长是解题的关键．
2．C
【分析】
如图所示过点P作PE⊥x轴于点E，由抛物线上任意一点到定点F（0，2）的距离与到x轴的距离相等，得到PE=PF，则△PMF的周长=FM+PM+PF，则要使△PMF周长最小，则PM+PF最小，即PM+PE最小，故当P、M、E三点共线时，PM+PE的值最小，最小为ME，由此求解即可．
解：如图所示过点P作PE⊥x轴于点E，
∵抛物线上任意一点到定点F（0，2）的距离与到x轴的距离相等，
∴PE=PF，
∴△PMF的周长=FM+PM+PF，
∴要使△PMF周长最小，则PM+PF最小，即PM+PE最小，
∴当P、M、E三点共线时，PM+PE的值最小，最小为ME，
∵M坐标为（3，6），
∴ME=6，
∴PF+PM=6
∵F（0，2），
∴
∴△PMF周长的最小值=ME+FM=6+5=11，
故选C．
【点拨】本题主要考查了二次函数的最短路径问题，两点距离公式，解题的关键在于能够准确读懂题意得到PE=PF．
3．D
解：如图，点A关于y轴的对称点A′的横坐标为﹣1，
连接A′B与y轴相交于点C，点C即为使AC+BC最短的点，
当x＝﹣1时，y＝﹣1，
当x＝2时，y＝﹣4，
所以，点A′（﹣1，﹣1），B（2，﹣4），
设直线A′B为



当x=0时，y=-2
即C（0，-2）
故选D
【点拨】本题考查了轴对称确定最短路线问题，二次函数的性质，熟记确定出最短路径的方法和二次函数的对称性确定出点C的位置是解题的关键．
4．C
【分析】
根据抛物线的性质和平移，以及一动点到两定点距离之和最小问题的处理方法，对选项进行逐一分析即可.
解：①抛物线的顶点，则抛物线与直线y＝3有且只有一个交点，正确，符合题意；
②抛物线x轴的一个交点在2和3之间，
则抛物线与x轴的另外一个交点坐标在x＝0或x＝﹣1之间，
则点N是抛物线的顶点为最大，点P在x轴上方，点M在x轴的下放，
故y1＜y3＜y2，故错误，不符合题意；
③y＝﹣x2+2x+2＝﹣（x+1）2+3，将该抛物线先向左，再向下均平移2个单位，
所得抛物线解析式为y＝（x+1）2+1，正确，符合题意；
④点A关于x轴的对称点，连接A′B交x轴于点D，
则点D为所求，距离最小值为BD′＝＝，
正确，符合题意；
故选：C．
【点拨】本题考查抛物线的性质、平移和距离的最值问题，其中一动点到两定点距离之和最小问题比较巧妙，属综合中档题.
5．A
【分析】
因为O与D关于直线PB的对称，所以PB垂直平分OD，则CO=CD，因为，△ACD的周长=AC+CD+AD=AC+CO+AD=AO+AD，AO=，所以当AD最小时，△ACD的周长最小；根据垂线段最短，可知此时点D与E重合，其横坐标为2，故m=1．
解：∵O与D关于直线PB的对称，
∴PB垂直平分OD，
∴CO=CD，
∵△ACD的周长=AC+CD+AD=AC+CO+AD=AO+AD，AO=，
∴当AD最小时，△ACD的周长最小；
∴此时点D与E重合，其横坐标为2，故m=1．
故选A.
【点拨】此题考查中心对称，垂直平分线的性质，垂线的性质，解题关键在于掌握运算法则.
6．D
【分析】
把A、B两点坐标代入抛物线的解析式并整理即可判断①②；
根据抛物线的顶点和最值即可判断③；
求出当△ABC是等腰直角三角形时点C的坐标，进而可求得此时a的值，于是可判断④；
根据利用对称性求线段和的最小值的方法（将军饮马问题）求解即可判断⑤.
解：把A（﹣3，0），B（1，0）代入y＝ax2+bx+c得到，消去c得到2a﹣b＝0，故①②正确；
∵抛物线的对称轴是直线x＝﹣1，开口向下，∴x＝﹣1时，y有最大值，最大值＝a﹣b+c，
∵m≠﹣1，∴a﹣b+c＞am2+bm+c，∴a﹣b＞am2+bm，故③正确；
当△ABC是等腰直角三角形时，C（﹣1，2），
可设抛物线的解析式为y＝a（x+1）2+2，把（1，0）代入解得a＝﹣，故④正确，
如图，连接AD交抛物线的对称轴于P，连接PB，则此时△BDP的周长最小，最小值＝PD+PB+BD＝PD+PA+BD＝AD+BD，
∵AD＝＝3，BD＝＝，
∴△PBD周长最小值为3，故⑤正确．
故选D．
【点拨】本题考查了二次函数的图象与性质、二次函数的图象与其系数的关系、待定系数法求二次函数的解析式和求三角形周长最小值的问题，熟练掌握二次函数的图象与性质是解题的关键.
7．A
【分析】
写出周长的解析式，用配方法表示顶点式，即可得出周长的最大值.
解：设P(x，x2﹣x﹣4)，
四边形OAPB周长＝2PA+2OA＝﹣2(x2﹣x﹣4)+2x＝﹣2x2+4x+8＝﹣2(x﹣1)2+10，
当x＝1时，四边形OAPB周长有最大值，最大值为10.
故选A．
【点拨】考核知识点：二次函数的最值运用.用配方法表示出顶点式，得出周长的最大值是解题的关键.
8．A
【分析】
抛物线y＝－x2＋px＋q的对称轴为x＝﹣3，可求得p=－6， 抛物线y＝－x2＋px＋q过点N（﹣1，1），可以求得：q=﹣4，得到抛物线解析式为：y＝－x2－6x﹣4，点M（﹣3,5），直线y＝kx＋b过M，N两点，其解析式为：y＝﹣2x＋3，作点A使得A与N关于y轴对称，连接MA，与y轴交于点P，易得P（0，2），作点B使得B与N关于x轴对称，连接MB，与x轴交于点Q，易得Q（），MA