人教版九年级数学上册 24.25 切线长定理（基础篇）（专项练习）

这是一份人教版九年级数学上册 24.25 切线长定理（基础篇）（专项练习），共25页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．用尺规作图作三角形的内切圆，用到了哪个基本作图（ ）
A．作一条线段等于已知线段B．作一个角等于已知角
C．作一个角的平分线D．作一条线段的垂直平分线
2．一个等腰直角三角形的内切圆与外接圆的半径之比为（ ）
A．B．C．D．
3．已知三角形的周长为12，面积为6，则该三角形内切圆的半径为（ ）
A．4B．3C．2D．1
4．如图，、是的切线，是的直径，，则的度数为（ ）
A．B．C．D．
5．如图，从⊙O外一点P引圆的两条切线PA，PB，切点分别是A，B，若∠APB＝60°，PA＝5，则弦AB的长是（ ）
A．B．C．5D．5
6．如图，PA和PB是⊙O的两条切线，A，B为切点，点D在AB上，点E，F分别在线段PA和PB上，且AD＝BF，BD＝AE．若∠P＝α，则∠EDF的度数为（ ）
A．90°﹣αB．αC．2αD．90°﹣α
7．如图，已知、是的两条切线，、为切点，连接交于，交于，连接、，则图中等腰三角形、直角三角形的个数分别为（ ）
A．1，2B．2，2
C．2，6D．1，6
8．若的外接圆半径为R，内切圆半径为，则其内切圆的面积与的面积比为（ ）
A．B．C．D．
9．已知△ABC中，∠ACB＝90°，CD、CE分别是△ABC中线和高线，则（ ）
A．D点是△ABC的内心B．D点是△ABC的外心
C．E点是△ABC的内心D．E点是△ABC的外心
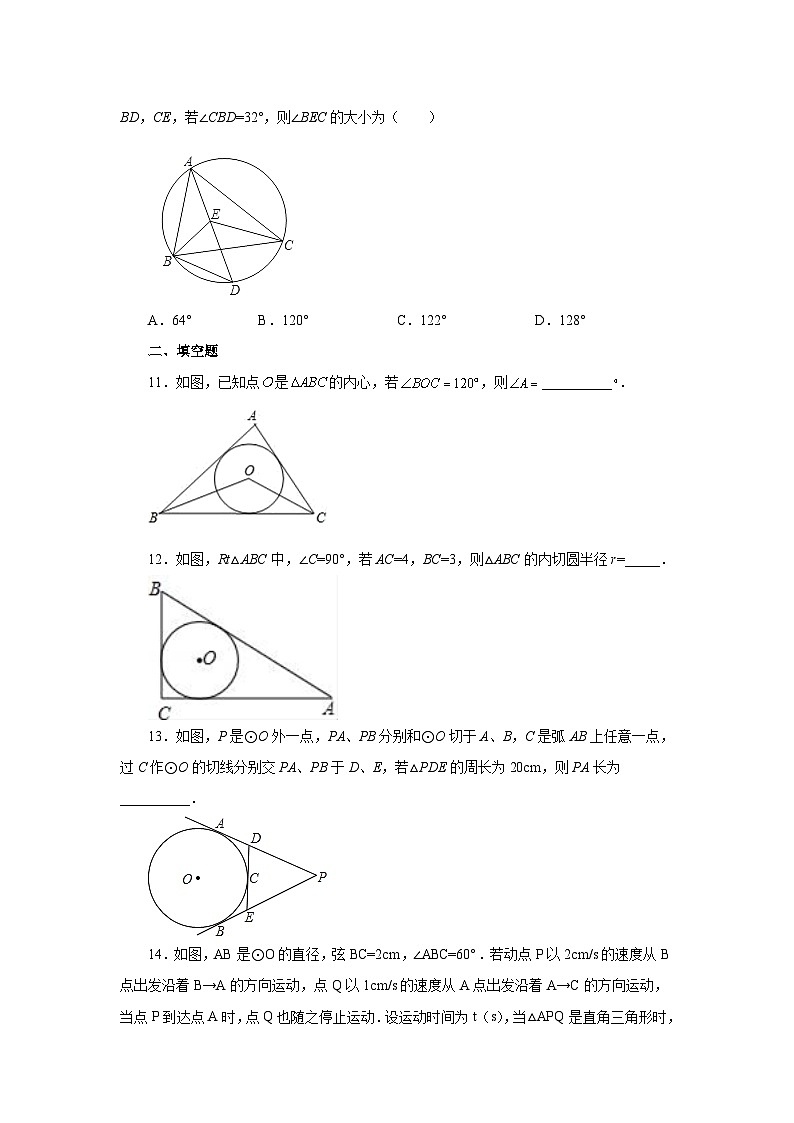
10．如图，点E是△ABC的内心，AE的延长线和△ABC的外接圆相交于点D，连接BD，CE，若∠CBD=32°，则∠BEC的大小为（ ）
A．64°B．120°C．122°D．128°
二、填空题
11．如图，已知点是的内心，若，则__________．
12．如图，Rt△ABC中，∠C=90°，若AC=4，BC=3，则△ABC的内切圆半径r=_____．
13．如图，P是⊙O外一点，PA、PB分别和⊙O切于A、B，C是弧AB上任意一点，过C作⊙O的切线分别交PA、PB于D、E，若△PDE的周长为20cm，则PA长为__________．
14．如图，AB是⊙O的直径，弦BC=2cm，∠ABC=60°．若动点P以2cm/s的速度从B点出发沿着B→A的方向运动，点Q以1cm/s的速度从A点出发沿着A→C的方向运动，当点P到达点A时，点Q也随之停止运动．设运动时间为t（s），当△APQ是直角三角形时，t的值为_________．
15．如图所示，AB、AC为⊙O的切线，B和C是切点，延长OB到D，使BD＝OB，连接AD．∠DAC＝78°，那么∠AOD等于_____度．
16．如图，是的切线，为切点，连接．若，则=__________．
17．在菱形ABCD中，对角线AC与BD相交于点O，AC=8、BD=6，则菱形ABCD的内切圆半径为 ________．
18．如图，四边形为的内接四边形，是的内心，点与点关于直线对称，则的度数是__________．
三、解答题
19．如图，中，，点O是的内心．求的度数．
20．如图，Rt中，，为上一点，以为圆心，长为半径的圆恰好与相切于点，交于点，连接，并延长交于点．
(1)求证：；
(2)若，，求的半径及的长．
21．如图，线段AB经过的圆心O，交圆O于点A，C，，AD为的弦，连接BD，，连接DO并延长交于点E，连接BE交于点M．
(1)求证：直线BD是的切线；
(2)求线段BM的长．
22．如图，点E是的内心，AE的延长线和的外接圆相交于点D，过D作直线DGBC．
(1)若，则______； ______．
(2)求证：；
(3)求证：DG是的切线C．
23．如图，在中，，以AB为直径的交BC于点P，交CA的延长线于点D，连接BD．
(1)求作的切线PQ，PQ交AC于点Q；（要求：尺规作图，不写作法，保留作图迹）
(2)在（1）的条件下，求证：．
24．如图，四边形ABCD是⊙O的内接四边形，AB = 6，BC = 8，∠ABC = 90°，弧AD = 弧DC．
(1)求边CD的长；
(2)已知△ABE与△ABD关于直线AB对称．
①尺规作图:作△ABE；（保留作图痕迹，不写作法）
②连接DE，求线段DE的长．
参考答案
1．C
【分析】
根据三角形内心的定义解答．
解：三角形的内切圆的圆心叫三角形的内心，是三角形三个角平分线的交点，
∴用尺规作图作三角形的内切圆，用到了作角的平分线的作法，
故选：C．
【点拨】此题考查了三角形内心的定义，正确理解定义是解题的关键．
2．D
【分析】
设等腰直角三角形的直角边是1，则其斜边是．根据直角三角形的内切圆半径是两条直角边的和与斜边的差的一半，得其内切圆半径是；其外接圆半径是斜边的一半，得其外接圆半径是．所以它们的比为=．
解：设等腰直角三角形的直角边是1，则其斜边是；
∵内切圆半径是，
外接圆半径是，
∴所以它们的比为=．
故选：D．
【点拨】本题考查三角形的内切圆与外接圆的知识，解题的关键是熟记直角三角形外接圆的半径和内切圆的半径公式：直角三角形的内切圆半径等于两条直角边的和与斜边的差的一半；直角三角形外接圆的半径是斜边的一半．
3．D
【分析】
设内切圆的半径为r，根据公式：，列出方程即可求出该三角形内切圆的半径．
解：设内切圆的半径为r
解得：r=1
故选D．
【点拨】此题考查的是根据三角形的周长和面积，求内切圆的半径，掌握公式：是解决此题的关键．
4．B
【分析】
(1)根据切线长定理推出AP=BP,根据等腰三角形性质和三角形的内角和定理求出
∠PAB=59°,求出∠BAC∠BOC即可.
解：PA,PB是⊙O的切线,
AP=BP,
∠P=62°,∠PAB==59°,
AC是⊙O的直径,
∠PAC=90°,
∠BAC=90°-59°=31°，
∠BOC=2∠BAC=62°，
故选B.
【点拨】本题考查了等腰三角形的性质,切线长定理,切线的性质,圆周角定理等知识点的应用,题型较好,综合性比较强,通过做此题培养了学生分析问题和解决问题的能力.
5．C
【分析】
先利用切线长定理得到PA=PB，再利用∠APB=60°可判断△APB为等边三角形，然后根据等边三角形的性质求解．
解：∵PA，PB为⊙O的切线，
∴PA=PB，
∵∠APB=60°，
∴△APB为等边三角形，
∴AB=PA=5．
故选：C．
【点拨】本题考查了切线长定理以及等边三角形的判定与性质．此题比较简单，注意掌握数形结合思想的应用．
6．D
【分析】
根据切线性质，证得≌，通过等量代换得出，再根据等腰三角形的性质，由∠P＝α，求得即可．
解： ∵PA和PB是⊙O的两条切线，A，B为切点，
∴PA=PB，
∴，即
在与中，
∵
∴≌（SAS），
∴，
在中，
,
∵，
∴，
∵，
∴，
∵∠P＝α，PA=PB，
∴
∴在中，，即，
∵，
∴
故选：D．
【点拨】本题考查了切线的性质，全等三角形的性质以及等腰三角形的性质，通过全等证明，等量代换求得是解题关键．
7．C
【分析】
根据切线长定理及半径相等得，△APB为等腰三角形，△AOB为等腰三角形，共两个；
根据切线长定理和等腰三角形三线合一的性质，直角三角形有：△AOC，△AOP，△APC，△OBC，△OBP，△CBP，共6个．
解：因为OA、OB为圆O的半径，所以OA＝OB，所以△AOB为等腰三角形，
根据切线长定理，PA＝PB，故△APB为等腰三角形，共两个，
根据切线长定理，PA＝PB，∠APC＝∠BPC，PC＝PC，所以△PAC≌△PBC，
故AB⊥PE，根据切线的性质定理∠OAP＝∠OBP＝90°，
所以直角三角形有：△AOC，△AOP，△APC，△OBC，△OBP，△CBP，共6个．
故选C．
【点拨】此题综合考查了切线的性质和切线长定理及等腰三角形的判定，有利于培养同学们良好的思维品质．
8．B
【分析】
画好符合题意的图形，由切线长定理可得：结合勾股定理可得：再求解直角三角形的面积，从而可得直角三角形的内切圆的面积与直角三角形的面积之比．
解：如图，由题意得：
，
由切线长定理可得：

设
，
，

而



故选B．
【点拨】本题考查的是三角形的内切圆与三角形的外接圆，切线长定理，勾股定理的应用，掌握以上知识是解题的关键．
9．B
【分析】
根据直角三角形斜边上的中线等于斜边的一半，可得是△ABC的外心，据此即可求解．
解：在△ABC中，∠ACB＝90°，
∵CD是△ABC中线，
∴D点是△ABC的外心．
故选：B．
【点拨】本题考查了三角形的外心，直角三角形斜边上的中线等于斜边的一半，掌握以上知识是解题的关键．
10．C
【分析】
根据圆周角定理可求∠CAD=32°，再根据三角形内心的定义可求∠BAC，再根据三角形内角和定理和三角形内心的定义可求∠EBC+∠ECB，再根据三角形内角和定理可求∠BEC的度数．
解：在⊙O中，
∵∠CBD=32°，
∴∠CAD=32°，
∵点E是△ABC的内心，
∴∠BAC=64°，
∴∠EBC+∠ECB=(180°-64°)÷2=58°，
∴∠BEC=180°-58°=122°．
故选：C．
【点拨】本题考查了三角形的内心，圆周角定理，三角形内角和定理，关键是得到∠EBC+∠ECB的度数．
11．60
【分析】
先利用，可求出∠OBC＋∠OCB，再利用三角形的内心即为三个内角角平分线的交点，可求出∠ABC＋∠ACB，然后就可求出∠A.
解：∵
∴∠OBC＋∠OCB=180°－∠BOC =60°
又∵点是的内心
∴BO、CO分别平分∠ABC和∠ACB
∴∠ABC＋∠ACB=2（∠OBC＋∠OCB） =120°
∴∠A=180°－（∠ABC＋∠ACB） =60°
故答案为60
【点拨】此题考查的是三角形内心的定义和三角形内角和定理.
12．1
解：如图，设△ABC的内切圆与各边相切于D，E，F，连接OD，OE，OF，
则OE⊥BC，OF⊥AB，OD⊥AC，
设半径为r，CD=r，
∵∠C=90°，AC=4，BC=3，
∴AB=5，
∴BE=BF=3﹣r，AF=AD=4﹣r，
∴4﹣r+3﹣r=5，
∴r=1，
∴△ABC的内切圆的半径为 1，
故答案为1．
13．10cm
【分析】
根据切线长定理，可将△PDE的周长转化为两条切线长的和，已知了△PDE的周长，即可求出切线的长．
解：根据切线长定理得：
AD＝CD，CE＝BE，PA＝PB，
则△PDE的周长＝
2PA＝20，
PA＝10．
故答案为：
【点拨】本题考查的是切线长定理，三角形的周长的计算，掌握切线长定理是解题的关键
14．或3-
解：因为AB是⊙O的直径，所以∠ACB=90°，又因为BC=2，∠ABC=60°；所以AB=2BC=4cm；因为运动时间为t（s），所以AQ=t，BP=2t，所以AP=4-2t，
①当∠AQP=90°时， 因为∠A=30°，AP=4-2t，所以PQ=2-t，AQ=PQ，所以t=（2-t），所以t=3-；②当∠APQ=90°时，PQ=AQ，AP=PQ，所以4-2t=，解得t=，
综上所述，当t的值为或3-时，△APQ是直角三角形．
【点拨】1．圆的性质；2．直角三角形的判定与性质．
15．64
【分析】
由已知条件推导出∠CAO=∠OAB=∠BAD，∠ABD=90°，由此根据∠DAC=78°，能求出∠AOD的大小．
解：∵AB、AC为⊙O的切线，B和C是切点，BD=OB，
垂直平分,∠CAO=∠OAB
∠OAB=∠BAD，
∴∠CAO=∠OAB=∠BAD，∠ABD=90°，
∵∠DAC=78°，
∴∠BAO=∠DAC=26°，
∴∠AOD=90°-26°=64°．
故答案为：64．
【点拨】本题考查角的大小的求法，解题时要认真审题，注意切线性质的灵活运用是解题的关键．
16．65°
【分析】
根据切线长定理即可得出AB=AC，然后根据等边对等角和三角形的内角和定理即可求出结论．
解：∵是的切线，
∴AB=AC
∴∠ABC=∠ACB=（180°－∠A）=65°
故答案为：65°．
【点拨】此题考查的是切线长定理和等腰三角形的性质，掌握切线长定理和等边对等角是解决此题的关键．
17．##2.4
【分析】
根据菱形的性质，可得AC⊥BD， ，再由勾股定理可得，然后设菱形ABCD的内切圆半径为r，根据三角形的面积，即可求解．
解：在菱形ABCD中，AC⊥BD， ，
∵AC=8、BD=6，
∴AO=4，DO=3，
∴ ，
设菱形ABCD的内切圆半径为r，
∴ ，
∵，
∴ ，解得： ，
即菱形ABCD的内切圆半径为．
故答案为：
【点拨】本题主要考查了菱形的性质，内切圆，熟练掌握菱形的性质是解题的关键．
18．
【分析】
连接OB、OD、BI、DI，利用轴对称的性质证得四边形OBID是菱形，得到∠BOD=∠BID，∠OBD=∠BDO=∠IBD=∠IDB，根据圆周角定理得到∠BOD=2∠A，由圆内接四边形性质得到，求出∠BID=180°-，由此得到2∠A=180°-，求出∠A=．
解：连接OB、OD、BI、DI，
∵点与点关于直线对称，
∴OB=BI，OD=DI，
∵OB=OD，
∴OB=BI=OD=DI，
∴四边形OBID是菱形，
∴∠BOD=∠BID，∠OBD=∠BDO=∠IBD=∠IDB，
∵∠BOD=2∠A，∠BID=180°-（∠IBD+∠IDB），
∵∠IBD+∠IDB=，,
∴ ∠IBD+∠IDB=，
∴∠BID=180°-，
∴2∠A=180°-，
解得∠A=，
故答案为：．
【点拨】此题考查了圆内接四边形对角互补的性质，三角形内心定义，菱形的判定及性质，三角形内角和定理，轴对称的性质，熟记各知识点是解题的关键．
19．117.5°
【分析】
由点是的内心，，，根据三角形的内心是三角形三条角平分线的交点，即可求得与的度数，又由三角形内角和定理，即可求得的度数．
解：点是的内心，，，
，，
．
【点拨】此题考查了三角形内心的性质．此题难度不大，解题的关键是掌握三角形的内心是三角形三条角平分线的交点．
20．(1)见分析(2)的半径为1.5，
【分析】
（1）连接DE，根据切线长定理可得∠BAO=∠DAO，∠PDC=90°，从而得到∠BAO=∠BAD，从而得到∠BAO==∠F，即可求证；
（2）根据切线长定理可得AB=AD=3，再由勾股定理可得BC=4，设的半径为x，则OD=x，OC=4-x，在中，由勾股定理可得的半径为1.5，由（1）可得，在中，由勾股定理，即可求解．
(1)证明：如图，连接DE，
∵，
∴AB与相切，
∵AD与相切，
∴∠BAO=∠DAO，∠PDC=90°，
∴∠BAO=∠BAD，
∵∠BAD=90°-∠C，∠C=90°-∠COD，
∴∠BAO==∠F；
(2)解：∵AB与相切，AD与相切，
∴AB=AD=3，
∵CD=2，
∴AC=5，
∴BC=4，
设的半径为x，则OD=x，OC=4-x，
在中，由勾股定理得：，
∴，解得：x=1.5，
∴的半径为1.5，即OB=1.5，
∵DF为直径，DF=3，
∴∠DEF=90°，
∵，
∴，
∴EF=2DE，
在中，由勾股定理得：，
∴，解得：或（舍去）．
【点拨】本题主要考查了切线长定理，圆周角定理，勾股定理，熟练掌握切线长定理，圆周角定理是解题的关键．
21．(1)见分析(2)
【分析】
（1）根据圆周角定理可得，从而得到 ，即可求证；
（2）连接DM，Rt△BOD中，根据直角三角形的性质可得 BO=2OD，从而得到，，再由的直径，可得，，从而得到，再由，可得，再由勾股定理，即可求解．
(1)证明：∵∠BOD=2∠BAD，
∴，
又∵，
∴ ，即，
又∵为的半径，
∴直线BD是的切线；
(2)解：如图，连接DM，
Rt△BOD中，，
∴，
又，，
∴，
∴，
∵的直径，
∴，，
在Rt△BDE中，，
∵，
∴，
在Rt△BDM中，．
【点拨】本题主要考查了切线的判定，圆周角定理，直角三角形的性质，勾股定理等知识，熟练掌握切线的判定，圆周角定理，直角三角形的性质，勾股定理是解题的关键．
22．(1)80°，130°；(2)见分析过程；(3)见分析过程．
【分析】
（1）由圆周角定理可得∠ACB＝∠ADB＝70°，由三角形的内心的性质可得∠AEB＝125°；
（2）由三角形的内心的性质可得AE平分∠BAC，BE平分∠ABC，可得∠BAE＝∠CAE，∠ABE＝∠CBE，由外角的性质可得∠BED＝∠DBE，可证DE＝CD；
（3）由垂径定理可得OD⊥BC，由平行线的性质可得OD⊥DG，可得结论．
(1)解：如图，连接BD，OD，
∵，
∴∠ACB＝∠ADB＝80°，
∴∠ABC+∠BAC＝100°，
∵点E是△ABC的内心，
∴AE平分∠BAC，BE平分∠ABC，
∴∠BAE＝∠CAE，∠ABE＝∠CBE，
∴∠BAE+∠ABE＝50°，
∴∠AEB＝130°，
故答案为：80°，130°；
(2)证明：∵∠BAE＝∠CAE，
∴＝，
∴BD＝CD，
∵∠BAE＝∠CAE＝∠CBD，∠ABE＝∠CBE，
∴∠BED＝∠BAE+∠ABE＝∠CBD+∠CBE＝∠DBE，
∴BD＝DE，
∴DE＝CD；
(3)证明：∵＝，
∴OD⊥BC，
∵DG∥BC，
∴OD⊥DG，
又∵OD是半径，
∴DG是⊙O的切线．
【点拨】本题考查了三角形的内心，圆的有关性质，切线的判定和性质，灵活运用这些性质解决问题是解题的关键．
23．(1)见详解；(2)见详解．
【分析】
（1）作射线OP，以点P为圆心，任意长为半径画弧交射线于M，N，以点M，N为圆心，大于为半径画弧，两弧交于点E，作直线PE，交AC于点Q，则直线PQ即为所求；
（2）如图，连接AP，则BP=PC，根据中位线的性质证得，由切线的性质，平行线的性质证，根据直径所对的圆周角是直角，得，证得问题得证．
(1)解：如图所示，直线PQ即为所求；
(2)证明：如图，连接AP，
，
，
，
，
是的切线，
，
，
是的直径，
，，
，
，
.
【点拨】本题考查了圆的综合题、圆的半径相等、切线的判定和性质、直径所对的圆周角是直角、三角形中位线的判定和性质、平行线的判定和性质、等腰三角形的性质等知识，作辅助线是解决本题的关键．
24．(1)(2)①图见分析②14
【分析】
（1）先求出直径AC，再得到△ADC是等腰直角三角形，利用勾股定理即可求解；
（2）①以B点为圆心，BD为半径，和以A点为圆心，AD为半径画弧，交点为E点，再顺次连接即可；
②过A点作AH⊥BD，先求出BD的长，再证明△BDE是等腰直角三角形，故可求出DE的长．
解：(1)∵AB = 6，BC = 8，∠ABC = 90°，
∴AC=，AC是⊙O的直径
∴∠ADC=90°
∵弧AD = 弧DC
∴AD=CD
∴△ADC是等腰直角三角形
∴AD2+CD2=AC2
解得CD=；
(2)①如图，△ABE为所求；
②过A点作AH⊥BD，
∵弧AD = 弧DC
∴∠ABD=∠CBD=∠ABC=45°
∴△ABH是等腰直角三角形
∵AB2=BH2+AH2，AH=BH
∴AH=BH=3
∵AD=CD=5
∴在Rt△ADH中，DH=
∴BD=BH+DH=
∵△ABE与△ABD关于直线AB对称
∴∠EBD=2∠ABD=90°，BE=BD=
∴△BDE是等腰直角三角形
∴DE=．
【点拨】此题主要考查圆内的线段长度求解、尺规作图，解题的关键是熟知圆周角的性质、等腰直角三角形的判定与性质及对称性的应用．