人教版八年级上册11.3.2 多边形的内角和教学课件ppt

这是一份人教版八年级上册11.3.2 多边形的内角和教学课件ppt，共32页。PPT课件主要包含了情景引入，八卦阵简介，新知探究，典例精析，根据上面的求法填表，多边形内角和，···，n-3，n-2，多边形的内角和公式等内容，欢迎下载使用。

你能求出正八边形的内角和吗？
定义：古代中国的一种军事阵法起源：源自《易经》基本元素：八个方位，象征天地风雷水火山泽变阵：可根据实际情况进行变阵应用：在军事、文化、艺术等多领域有应用
三角形的内角和是多少？
三角形的内角和是 180°.
长方形的内角和是多少？
长方形的内角和是 360°.
任意四边形的内角和是多少？
猜想：四边形的内角和是 360°.
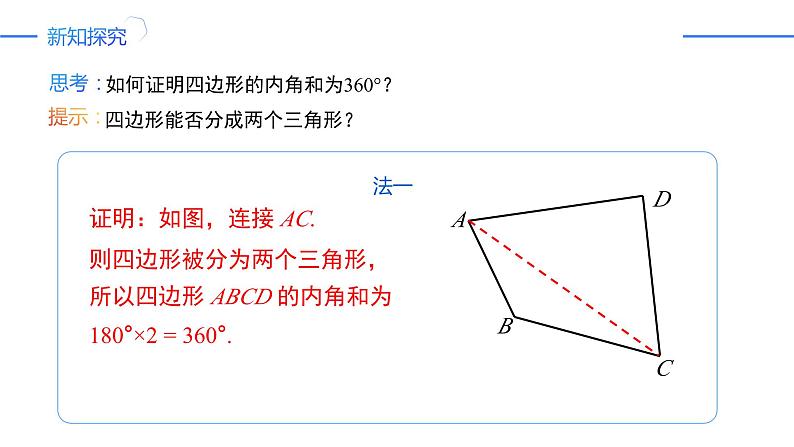
如何证明四边形的内角和为360°？
证明：如图，连接 AC.则四边形被分为两个三角形，所以四边形 ABCD 的内角和为180°×2 = 360°.
四边形能否分成两个三角形？
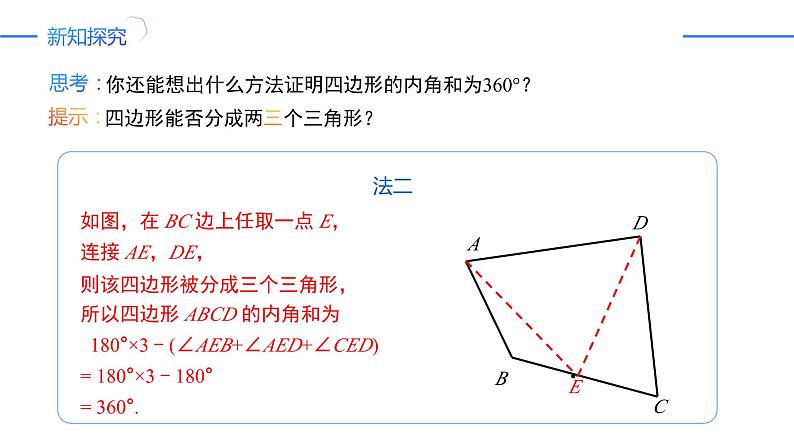
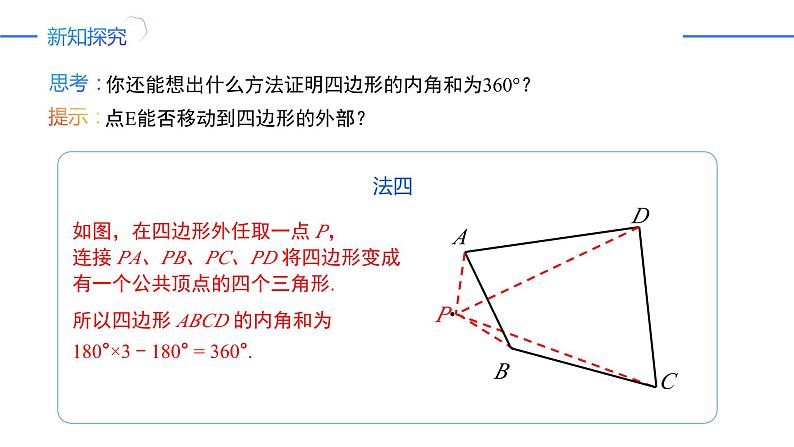
你还能想出什么方法证明四边形的内角和为360°？
四边形能否分成两三个三角形？
如图，在 BC 边上任取一点 E， 连接 AE，DE，则该四边形被分成三个三角形，所以四边形 ABCD 的内角和为 180°×3 - (∠AEB+∠AED+∠CED)= 180°×3 - 180°= 360°.
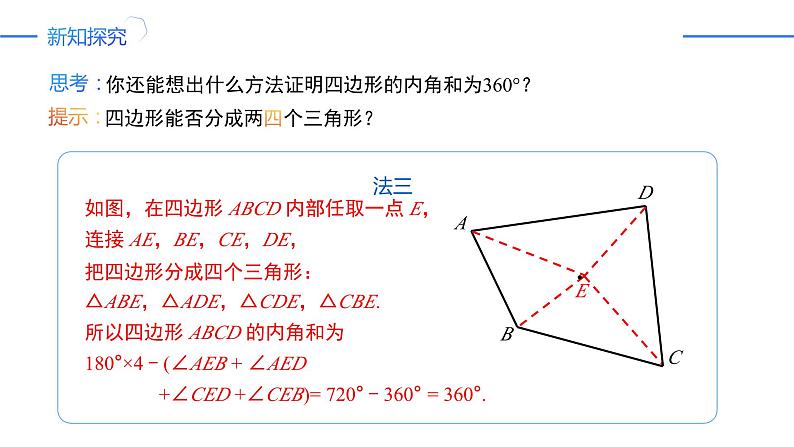
四边形能否分成两四个三角形？
如图，在四边形 ABCD 内部任取一点 E， 连接 AE，BE，CE，DE，把四边形分成四个三角形： △ABE，△ADE，△CDE，△CBE.所以四边形 ABCD 的内角和为180°×4 - (∠AEB + ∠AED +∠CED +∠CEB)= 720° - 360° = 360°.
点E能否移动到四边形的外部？
如图，在四边形外任取一点 P， 连接 PA、PB、PC、PD 将四边形变成 有一个公共顶点的四个三角形.
所以四边形 ABCD 的内角和为 180°×3 - 180° = 360°.
结论： 四边形的内角和为360°.
这四种方法都运用了转化与划归思想， 把四边形分割成三角形， 再用已学的三角形内角和定理求解.
求下列图形中 的值.
解：（1）根据四边形的内角和为360°可得，140+90+2x=360解得x=65（2）根据四边形的内角和为360°可得，120+80+75+x=360解得x=85
如图，在四边形 ABCD 中，∠A 与∠C 互补，BE 平分∠ABC，DF 平分∠ADC，若 BE∥DF，求证：△DCF 为直角三角形．
证明：∵ 在四边形 ABCD 中，∠A 与∠C 互补，∴∠ABC +∠ADC = 180°．∵ BE 平分∠ABC，DF 平分∠ADC，∴∠CDF +∠EBF = 90°．∵ BE∥DF，∴∠EBF = ∠CFD，∴∠CDF +∠CFD = 90°．∴△DCF 为直角三角形．
你能仿照求四边形内角和的方法，求五边形和六边形内角和吗?能否求出n边形的内角和？
内角和为 180°×3 = 540°.
把五边形分成3个三角形
3个三角形内角和是180°×3=540°
五边形内角和是540°
把六边形分成4个三角形
4个三角形内角和是180°×4=720°
六边形内角和是720°
内角和为 180°×4 = 720°.
分成的三角形个数都比多边形的边数少2。
可以把多边形分成若干个三角形，计算它的内角和。
分成了几个三角形，多边形的内角和就有几个180°。
你能用一个式子表示多边形内角和的计算方法吗？
（边数-2）×180 °
( n - 2 )·180°
1×180°=180°
2×180°=360°
3×180°=540°
4×180°=720°
回顾探索和发现规律的过程，说说你的体会.
多边形的内角和可以根据三角形的内角和推算出来.
从简单的问题想起、有序思考，是探索规律的有效方法.
可以把新的问题转化成能够解决的问题.
已知在一个十边形中，九个内角的和的度数是1290°，求这个十边形的另一个内角的度数.
解:这个十边形的内角和为（10－2）×180° =1440 °则十边形的另一个内角的度数为1440 °- 1290° =150 °
一个同学在进行多边形的内角和计算时，求得内角和为 1125°，当他发现错了以后，重新检查，发现少算了一个内角，问这个内角是多少度？他求的是几边形的内角和？
解：设此多边形的内角和为 x，则有 1125°＜x＜1125°＋180°，即 180°×6＋45°＜x＜180°×7＋45°.∵ x 为多边形的内角和，所以它是 180° 的倍数，∴ x＝180°×7＝1260°.∴ 7＋2＝9，1260°－1125°＝135°.因此，漏加的这个内角是 135°，这个多边形是九边形.
解题技巧：1°多边形的内角的度数在 0°~180° 之间. 2°多边形的内角和公式说明其内角和是180° 的整数倍.
每条边都相等的多边形我们称之为“正多边形”.正多边形的每个内角都相等，比如正三角形的每个内角都是60°，那么，正六边形的每个内角是多少度呢？
∴正六边形的每一个内角为720°÷6=120°答：正六边形的每个内角都是120°。
解：正六边形的内角和为（6-2）x180°=720°∵正六边形的每一个内角都相等
因为正多边形的每个角相等，所以知道正多边形的边数，就可以求出每一个内角的度数.
（n－2）×180°/ n
已知某正多边形的每个外角都是 72°，则这个多边形 是正____边形.
分析：因为正多边形的每一个外角都是72°，则这个正多边形的每一个内角都是180°-72°=108°，根据多边形内角和公式可得解得n =5因此这个多边形是正五边形.
( n - 2 )·180°=n ·108°
多边形的外角和它相邻的内角之间有什么关系？
如图所示五边形的外角和为多少？
5×180°-(5-2)×180°=360°
如图，在五边形的每个顶点处各取一个外角， 这些外角的和叫做五边形的外角和．
n 边形的外角和等于 360°.正n 边形的每一个外角都等于
－(n－2)×180°
= n 个平角和－ n 边形的内角和
n 边形的外角和又是多少呢？
外角和始终为定值，与边数无关
在 n 边形的每个顶点处各取一个外角，这些外角的和叫做 n 边形的外角和．
一个正多边形的一个外角比一个内角小90°，求这个多边形的每个内角的度数及边数．
解：设该正多边形的每个内角是 x°，相邻外角是 y°，则得到一个方程组 解得而任何多边形的外角和是 360°，则该正多边形的边数为 360÷45 = 8.故这个多边形的每个内角的度数是 135°，边数是八条．
如图，求∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7 的度数.
解：如图，∵∠3＋∠4＝∠8＋∠9，∴∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7＝∠1＋∠2＋∠8＋∠9＋∠5＋∠6＋∠7＝五边形的内角和＝540°.
(n - 2)×180° (n≥3 的整数)
1. 一个正多边形的内角和为 720°，则这个正多边形的每一个内角等于_____．
2.如图所示，小华从点 A 出发，沿直线前进 10 米后左转 24°，再沿直线前进 10 米，又向左转 24°，…，照这样走下去，他第一次回到出发地点 A 时，走的路程一共是______米．
3. 一个多边形的内角和不可能是（ ）A.450° B. 540° C. 720 ° D. 1980°
4. 一个多边形从一个顶点可引对角线 3 条，则这个多边形的内角和等于 ( )A. 360° B. 540° C. 720° D. 900°
5.求下列图形中的x的值.
解：x=[(5-2)×180-90-150-120]÷3=60
解：x=(5-2)×180-135-150-180=75
6.如果一个四边形的一组对角互补，那么另一组对角有什么关系？试说明理由.
如图，在四边形 ABCD 中， ∠A +∠C = 180°.
∠A +∠B +∠C +∠D = 360°，
∠B +∠D = 360° - (∠A +∠C ) = 360° - 180° = 180°.
如果一个四边形的一组对角互补，那么另一组对角也互补.
7.已知一个多边形，它的内角和等于外角和的 2 倍，求这个多边形的边数.
解： 设多边形的边数为 n. ∵ 它的内角和等于 (n－2) • 180°， 外角和等于 360°， ∴ (n－2) • 180° = 2×360°. 解得 n = 6. ∴ 这个多边形的边数为 6.