初中数学人教版八年级上册第十二章 全等三角形12.2 三角形全等的判定教课内容课件ppt

这是一份初中数学人教版八年级上册第十二章 全等三角形12.2 三角形全等的判定教课内容课件ppt，共25页。PPT课件主要包含了情景引入，知识回顾，新知探究，①只给一条边，不一定全等，②只给一个角，1三个角，2三条边，3两边一角，4两角一边等内容，欢迎下载使用。
学校举行艺术节，为了装扮会场，需要一定数量的用纸折成的玫瑰花，这些玫瑰花是有一些相同的三角形纸片折叠而成，为了准备这些三角形纸片，老师应该提供哪些数据才能保证所有同学剪裁的三角形纸片全等呢？
能够完全重合的两个三角形叫全等三角形.
全等三角形有什么性质：
全等三角形的对应边相等，对应角相等.
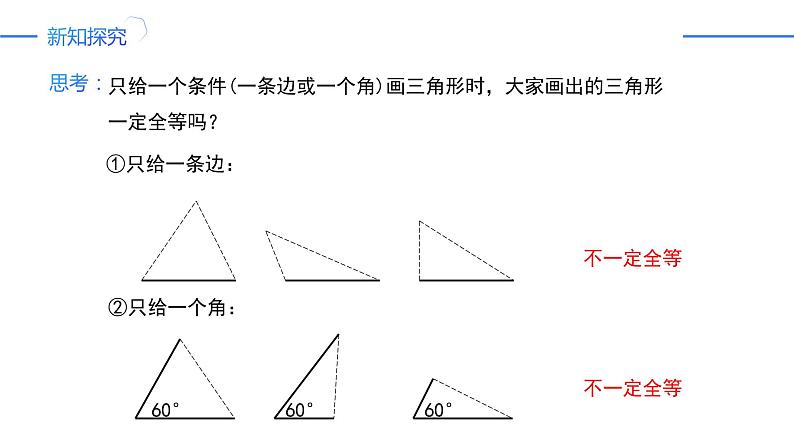
只给一个条件(一条边或一个角)画三角形时，大家画出的三角形 一定全等吗？
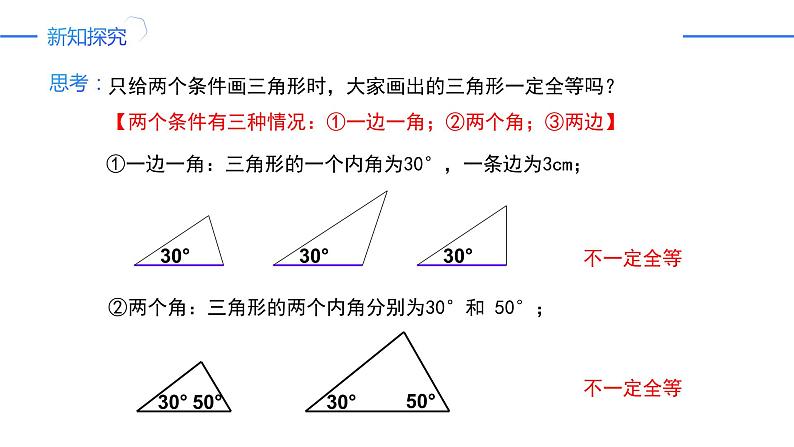
只给两个条件画三角形时，大家画出的三角形一定全等吗？【两个条件有三种情况：①一边一角；②两个角；③两边】
①一边一角：三角形的一个内角为30°，一条边为3cm；
②两个角：三角形的两个内角分别为30°和 50°；
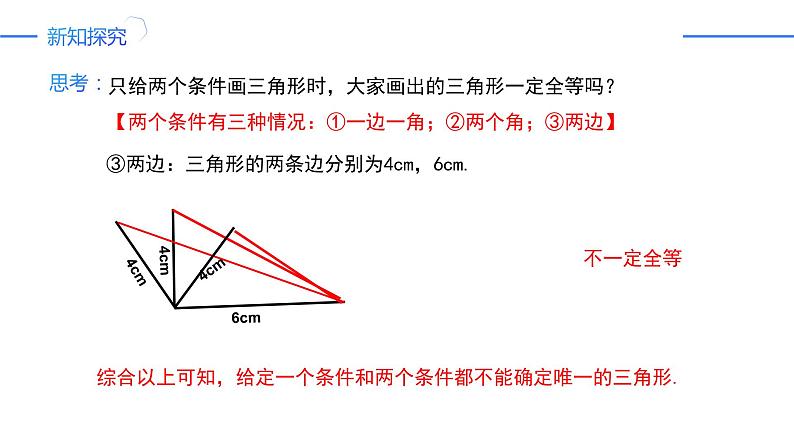
③两边：三角形的两条边分别为4cm，6cm.
综合以上可知，给定一个条件和两个条件都不能确定唯一的三角形.
如果给出三个条件画三角形，你能说出有哪几种可能的情况吗？
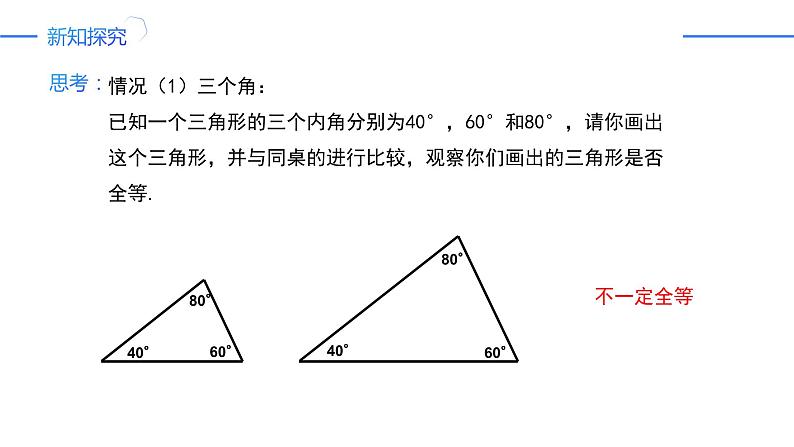
情况（1）三个角：已知一个三角形的三个内角分别为40°，60°和80°，请你画出这个三角形，并与同桌的进行比较，观察你们画出的三角形是否全等.
情况（2）三个边：已知一个三角形的三条边分别为4cm，5cm和7cm，请你画出这个三角形，并与同桌的进行比较，观察你们画出的三角形是否全等.
作图方法：(1) 画 线段 BC=7cm；(2) 分别以 B，C为圆心，4cm和5cm为半径画弧，两弧相交于点 A；(3) 连接 AB，AC.
通过作图我们发现，班上所有同学正确作出的三角形是全等的.
基本事实：三边分别相等的两个三角形全等． 简记为SSS. (或边边边)．
特别提醒：在做题时往往在相等的边或角上作相同的标记，方便辨别和判定全等三角形.
第一个三角形的名称和对应的判定条件
第二个三角形的名称和对应的判定条件
全等三角形的对应字母要写在对应的位置，顺序不能错
已知：如图，AB = AE，AC = AD，BD = CE.求证：△ABC≌△AED.
证明：∵ BD = CE，
∴ BD－CD = CE－CD.
∴ BC = ED.
在△ABC 和△AED 中，
AC = AD (已知)，AB = AE (已知)，BC = ED (已证)，
∴△ABC≌△AED (SSS).
1.有隐含条件的先找隐含条件
2.再找现有条件AB = AE，AC = AD
3.最后找准备条件BD = CEBC = ED
证全等时要用的条件要先证好
摆出三个条件用大括号括起来
已知: 如图，AC=AD ,BC=BD. 求证: ∠C＝∠D.
AC = FE (已知)， BC = DE (已知)， AB = FD (已证)，∴△ABC≌△FDE (SSS).
已知：如图 ，AC = FE，AD = FB，BC = DE.求证：(1)△ABC≌△FDE； (2) ∠C = ∠E.
证明：(1) ∵ AD = FB， ∴ AB = FD (等式的性质). 在△ABC 和△FDE 中，
(2)∵△ABC≌△FDE（已证）,
∴∠C =∠E (全等三角形的对应角相等).
已知：∠AOB．求作：∠A′O′B′ =∠AOB．
思考：如何用尺规作一个角等于已知角
作法： (1) 以点 O 为圆心，任意长为半径画弧， 分别交OA，OB 于点 C、D；(2) 画一条射线 O′A′，以点 O′ 为圆心，OC 长为 半径画弧，交 O′A′ 于点 C′；(3) 以点 C′ 为圆心，CD 长为半径画弧，与第 (2) 步中所画的弧交于点 D′；(4) 过点 D′ 画射线 O′B′，则∠A′O′B′ =∠AOB．
思考：以上尺规作图的依据是什么？
DO= D’O’(已知)， OC = O’C ’(已知)， DC = D’C ’ (已知)，∴△DOC≌△D’O’C ’ (SSS).
证明：在△DOC 和△D’O’C ’中，
∴∠O=∠O’ (全等三角形的对应角相等).
1.如图,E是AC上一点,AB=AD,BE=DE,可应用“SSS”证明三角形全等的是（ ） A. △ABC≌△ADC B. △ABE≌△ADE C. △CBE≌△CDE D. 以上选项都对
2. 如图，AB＝CD，AD＝BC，则下列结论： ①△ABC≌△CDB；②△ABC≌△CDA；③△ABD ≌△CDB；④ BA∥DC. 正确的个数是 ( ) A. 1 B. 2 C. 3 D. 4
3.如图，△ABC中，AD=DE，AB=BE，∠A=100°，则∠DEC= 度.
4.如图，在△ABC 和△FED中，AC = FD，BC = ED，利用“SSS”来判定△ABC和△FED全等时，下面的4个条件中：①AE=FB；②AB=FE；③AE=BE；④BF=BE，可利用的是_______.
5.如图，有一个三角形钢架，AB = AC，AD 是连接点 A 与 BC 中点 D 的支架.求证：(1)△ABD≌△ACD；(2)∠BAD = ∠CAD.
证明：∵ D 是 BC 中点， ∴ BD = CD． 在△ABD 与△ACD 中，
∴△ABD≌△ACD (SSS).
（2）由（1）得△ABD≌△ACD，∴ ∠BAD = ∠CAD (全等三角形对应角相等).
6.如图，点B，E，C，F在一条直线上，AB＝DE，AC＝DF，BE＝CF.证明：∠A＝∠D.
证明：∵BE＝CF，∴BE＋EC＝CF＋EC，即BC＝EF.在△ABC和△DEF中， 所以△ABC≌△DEF(SSS)．所以∠A＝∠D.
7.如图, 在四边形ABCD中，AD = CB，AB = CD. 求证：∠B = ∠D.
证明：在△ABC和△CDA 中，∵ CB = AD, AB = CD (已知)， AC = CA(公共边)，∴ △ABC≌△CDA().∴ ∠B =∠D(全等三角形的对应角相等).
8. 如图，AD＝BC，AC＝BD. 求证：∠C＝∠D.
证明：连接 A、B 两点.
∴△ABD≌△BAC (SSS).
AD = BC，BD = AC，AB = BA，
在△ABD 和△BAC 中，