初中数学人教版八年级上册13.1.1 轴对称复习课件ppt

这是一份初中数学人教版八年级上册13.1.1 轴对称复习课件ppt，共27页。PPT课件主要包含了思维导图，知识串讲，轴对称图形，对称轴，垂直平分线，x-y，-xy，1两腰相等，顶角平分线，等角对等边等内容，欢迎下载使用。
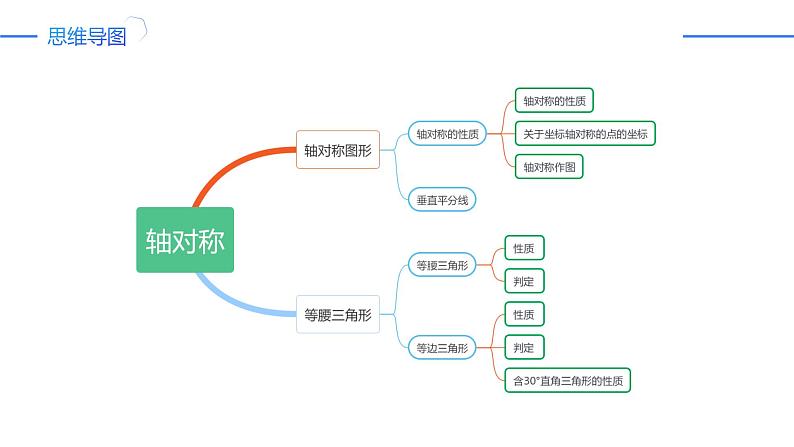
一、轴对称的相关定义和性质
(1) 如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做____________，这条直线就是它的_________.
(2) 将一个平面图形沿一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称，这条直线就是它们的对称轴.
(3) 轴对称图形的________，是任何一对对应点所连线段的垂直平分线.
(1) 关于某直线对称的两个图形是全等图形；
(2) 如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的____________；
二、垂直平分线的性质和判定
性质：线段垂直平分线上的点与这条线段两个端点的距离______.
判定：与线段两个______距离相等的点在这条线段的垂直平分线上．
点 (x，y) 关于 x 轴对称的点的坐标为 ；
三、平面直角坐标系中的轴对称
点 (x，y) 关于 y 轴对称的点的坐标为 .
四、等腰三角形的性质及判定
(4)___________、底边上的中线和底边上的高互相重合，简称“三线合一”.
(3) 两个_______相等，简称“等边对等角”；
(2) 是轴对称图形，等腰三角形的顶角平分线所在的直线是它的对称轴；
(1) 有两边相等的三角形是等腰三角形；
(2) 如果一个三角形中有两个角相等，那么这两个角所对的边也相等（简写成“____________”）.
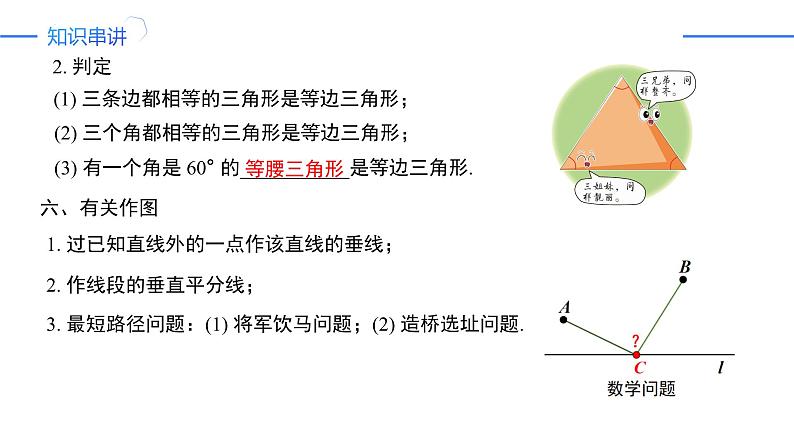
五、等边三角形的性质及判定
(1) 等边三角形的三边都相等；
(2) 等边三角形的三个内角都相等，并且每一个角都等于_____；
(3) 是轴对称图形，对称轴是三条高所在的直线；
(4) 任意角平分线、角对边上的中线、对边上的高互相重合，简称“三线合一”.
(5) 在直角三角形中，30° 角所对的直角边等于斜边的一半.
(1) 三条边都相等的三角形是等边三角形；
(2) 三个角都相等的三角形是等边三角形；
(3) 有一个角是 60° 的___________是等边三角形.
1. 过已知直线外的一点作该直线的垂线；
2. 作线段的垂直平分线；
3. 最短路径问题：(1) 将军饮马问题；(2) 造桥选址问题.
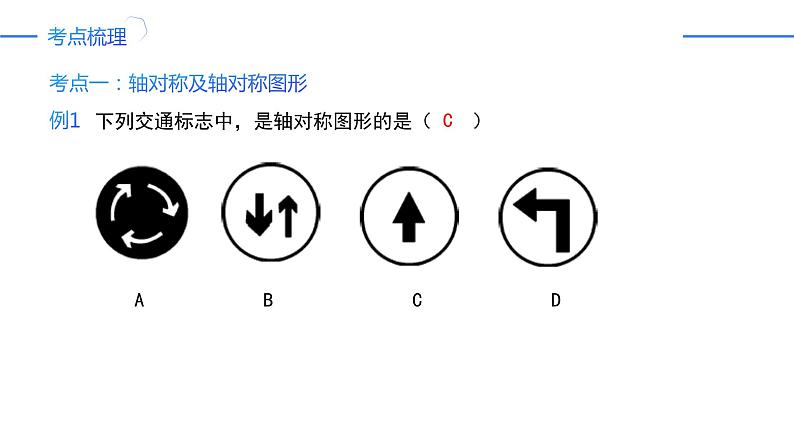
考点一：轴对称及轴对称图形
下列交通标志中，是轴对称图形的是（　　） A B C D
如图，如果直线l是多边形ABCDE的对称轴，其中∠A＝120°，∠C＝110°，那么∠CDE的度数等于（　　） A．40° B．60° C．70° D．80°
将一张矩形纸片叠成如图所示的图形，若AB=6cm，则AC=_____cm．
考点二：关于坐标轴对称的点的坐标
按要求完成作图：(1)作△ABC关于y轴对称的△A1B1C1；(2)在x轴上找出点P，使PA+PC最小，并直接写出P点的坐标：
已知点P1（a＋1，4）和P2（2，b）关于y轴对称，则a－b的值为（　　） A．－7 B．－1 C．1 D．5
点（－1，2）关于x轴对称的点的坐标是（　　） A．（1，2） B．（1，－2） C．（－1，－2） D．（2，－1） 点P（3，4）关于y轴对称的点的坐标是（　　） A．（3，－4） B．（－3，4） C．（－4，－3） D．（－4，3）
考点三：线段垂直平分线的性质和判定
如图，△ABC中，DE是AC的垂直平分线，AE＝10， △ABD的周长是40，则△ABC的周长是（　　） A．70 B．60 C．50 D．40
已知△ABC，∠BAC=110°，DE，FG分别是AB，AC的垂直平分线且DE交BC于M点，FG交BC于N点，求∠MAN的度数.
解：设∠B=x，∠C=y．∵∠BAC+∠B+∠C=180°，∴110°+∠B+∠C=180°，∴x+y=70°．∵AB、AC的垂直平分线分别交BA于E、交AC于G，∴DA=BD，FA=FC，∴∠EAD=∠B，∠FAC=∠C．∴∠DAF=∠BAC-（x+y）=110°-70°=40°．（2）∵AB、AC的垂直平分线分别交BA于E、交AC于G，∴DA=BD，FA=FC，∴△DAF的周长为：AD+DF+AF=BD+DF+FC=BC=10（cm）
如图，在△ABC中，AB、AC的垂直平分线分别交BC于点E、F，若∠BAC＝110°，则∠EAF为（　　） A．35° B．40° C．45° D．50°
如图，已知AC=AD，BC=BD，则（ ）
在△ABC中，AD是高，在线段DC上取一点E，使BD=DE， 已知AB+BD=DC.求证：E点在线段AC的垂直平分线上．
证明：∵AD是高，∴AD⊥BC，又∵BD=DE，∴AD所在的直线是线段BE的垂直平分线，∴AB=AE，∴AB+BD=AE+DE，又∵AB+BD=DC，∴DC=AE+DE，∴DE+EC=AE+DE∴EC=AE，∴点E在线段AC的垂直平分线上．
考点四：等腰三角形的性质和判定
如图，△ABC中，AB＝AC，AD⊥BC，下列结论中不正确的是（　　） A．D是BC中点 B．AD 平分∠BAC C．AB＝2BD D．∠B＝∠C
如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC＝BD. 求证：△OAB是等腰三角形．
长方形具有对边平行的特征，将长方形ABCD按如图所示折叠． （1）若∠FEC＝64°，求∠1的度数； （2）求证：△EFG是等腰三角形．
解：(1) 由折叠得∠GEF＝∠CEF＝64°，∴∠GEB＝52°，∵AD∥BC，∴∠1＝∠GEB＝52°.(2) 由折叠得∠GEF＝∠CEF，∵AD∥BC，∴∠GFE＝∠CEF，∴∠GEF＝∠GFE，∴EG＝FG，∴△EFG是等腰三角形．
如图，AB∥CD，E是BC的中点，DE平分∠ADC，延长DE交AB的延长线于F.（1）求证：△BFE≌△CDE；（2）求证：AE⊥DF.
(2) ∵AB∥CD，∴∠F＝∠CDE，∵DE平分∠ADC，∴∠CDE＝∠ADF，∴∠F＝∠ADF，∴AD＝AF，由(1)得△BFE≌△CDE，∴DE＝FE，∴AE⊥DF.
考点五：等边三角形的性质和判定
在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°，得到△BAE，连接ED，若BC=5，BD=4．则下列结论错误的是（　　）
如图，△ABC是等边三角形，BD平分∠ABC， 点E在BC的延长线上，且CE=1，∠E=30°， 则BC=_____．
如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB， 过点E作EF⊥DE，交BC的延长线于点F．（1）求∠F的度数； （2）若CD=2，求DF的长．
解： （1）∵△ABC是等边三角形，∴∠B=60°，∵DE∥AB，∴∠EDC=∠B=60°，∵EF⊥DE，∴∠DEF=90°，∴∠F=90°﹣∠EDC=30°；（2）∵∠ACB=60°，∠EDC=60°，∴△EDC是等边三角形．∴ED=DC=2，∵∠DEF=90°，∠F=30°，∴DF=2DE=4．
考点六：含30°角的直角三角形
如图，△ABC为等边三角形， DC∥AB，AD⊥CD于D，若CD＝2， 则AB的长度为　　　　　． 如图，在Rt△ABC中，∠C＝90°，∠B＝30°， AD是△ABC的角平分线， CD＝2，则BC＝　　　　　．
如图，等腰△ABC中，AB＝AC，∠BAC＝120°， AE⊥AC，DE垂直平分AB于D，若DE＝2， 则EC＝　　　　　． 如图，等边△ABC中，AD＝BD，过点D作DF⊥AC 于点F，过点F作FE⊥BC于点E，若AF＝6，则 线段BE的长为　　　　　．
如图，已知点D、点E分别是等边三角形ABC中BC、AB边的中点， AD=5，点F是AD边上的动点，则BF+EF的最小值为（　　）A．7.5 B．5 C．4 D．不能确定
解析：△ABC为等边三角形，点D是BC边的中点， 即点B与点C关于直线AD对称. ∵点F在AD上，故BF=CF. 即BF+EF的最小值可转化为求CF+EF的最小值， 故连接CE即可， 线段CE的长即为BF+EF的最小值.
如图，∠AOB＝30°，∠AOB内有一定点P，且OP＝10．若在OA、OB上分别有动点Q、R，则△PQR周长的最小值是( ) A．10 B．15 C．20 D．30
解析：过点P作关于OA，OB对称点P1，P2，连接P1P2，交OA于点Q，OB于点R，此时△PQR周长的最小，连接OP1 和OP2，可证△OP1 P2为等边三角形，边长为10．
模型一：平面几何三要素