广东省东莞市2023-2024学年八年级上学期期中数学试题

这是一份广东省东莞市2023-2024学年八年级上学期期中数学试题，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1．(3分)如图，人字梯中间一般会设计一“拉杆”，以增加使用梯子时的安全性，这样设计蕴含的数学依据是( )
A．两直线平行，内错角相等 B．垂线段最短 C．两点之间，线段最短 D．三角形具有稳定性
2．(3分)下列长度的各组线段，可以组成三角形的是( )
A．5，5，11 B．7，8，15 C．7，2，4 D．13，12，20
3．(3分)下列运算正确的是( )
A．a2﹣a＝a B．a2•a3＝a6 C．(a2)3＝a6 D．a9÷a3＝a3
4．(3分)下列从左边到右边的变形，属于因式分解的是( )
A．6a2b2＝3ab•2ab B．(x+1)(x﹣1)＝x2﹣1
C．x2﹣4x+4＝(x﹣2)2 D．x2﹣x﹣4＝x(x﹣1)﹣2
5．(3分)如果一个多边形的每一个内角都是135°，那么这个多边形的边数是( )
A．5 B．6 C．8 D．10
6．(3分)已知图中的两个三角形全等，则∠1等于( )
A．50° B．58° C．60° D．72°
7．(3分)如图，已知AB＝AD，添加下列一个条件后，仍无法判定△ABC≌△ADC的是( )
A．CB＝CD B．∠BCA＝∠DCA C．∠BAC＝∠DAC D．∠B＝∠D＝90°
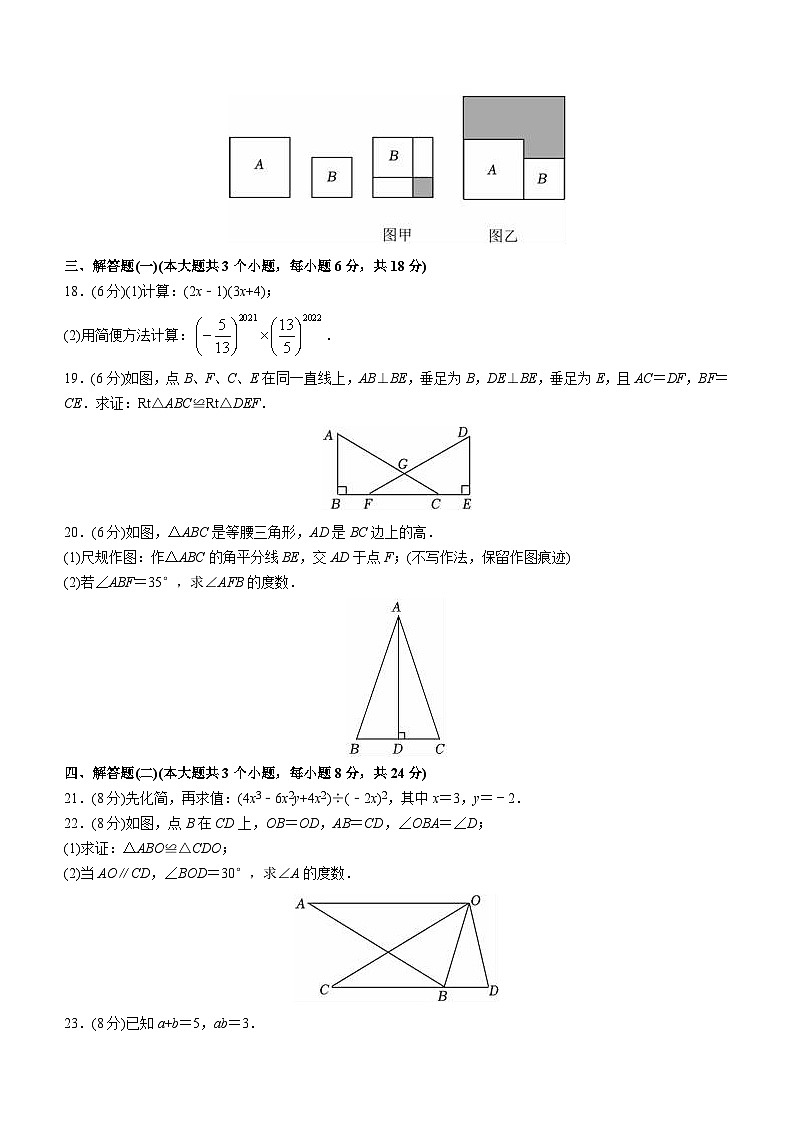
8．(3分)下列条件中：①∠A+∠B＝∠C，②∠A：∠B：∠C＝1：2：3，③∠A＝∠B＝∠C，④∠A＝90°﹣∠B能确定△ABC是直角三角形的有( )
A．①②③ B．①②④ C．②④ D．①②③④
9．(3分)下列各式中，不能运用平方差公式计算的是( )
A．(m﹣n)(﹣m﹣n) B．(﹣1+mn)(1+mn)
C．(﹣x+y)(x﹣y) D．(2a﹣b)(2a+b)
10．(3分)已知△ABC的内角∠A＝a，分别作内角∠ABC与外角∠ACD的平分线，两条平分线交于点A1，得∠A1；∠A1BC和∠A1CD的平分线交于点A2，得∠A2；…以此类推得到∠A2023的度数是( )
A． B． C． D．
二、填空题(本大题共7小题，每小题4分，共28分)
11．(4分)因式分解：2mn﹣6m＝ ．
12．(4分)一个三角形的两边长分别是2和3，若它的第三边长为奇数，则这个三角形的周长为 ．
13．(4分)如图，已知AE是△ABC的边BC上的中线，若AC＝6，△AEC的周长比△AEB的周长多1，则AB＝ ．
14．(4分)如图，由4个相同的小正方形组成的格点图中，∠1+∠2+∠3＝ 度．
15．(4分)若am＝3，an＝2，则am+n＝ ．
16．(4分)如图，在△ABC中，∠C＝90°，AB＝16，AD是△ABC的一条角平分线，若CD＝5，则△ABD的面积是 ．
17．(4分)有两个正方形A，B，现将B放在A的内部如图甲，将A，B并排放置后构造新的正方形如图乙．若图甲和图乙中阴影部分的面积分别为和，则正方形A，B的面积之和为 ．
三、解答题(一)(本大题共3个小题，每小题6分，共18分)
18．(6分)(1)计算：(2x﹣1)(3x+4)；
(2)用简便方法计算：．
19．(6分)如图，点B、F、C、E在同一直线上，AB⊥BE，垂足为B，DE⊥BE，垂足为E，且AC＝DF，BF＝CE．求证：Rt△ABC≌Rt△DEF．
20．(6分)如图，△ABC是等腰三角形，AD是BC边上的高．
(1)尺规作图：作△ABC的角平分线BE，交AD于点F；(不写作法，保留作图痕迹)
(2)若∠ABF＝35°，求∠AFB的度数．
四、解答题(二)(本大题共3个小题，每小题8分，共24分)
21．(8分)先化简，再求值：(4x3﹣6x2y+4x2)÷(﹣2x)2，其中x＝3，y＝﹣2．
22．(8分)如图，点B在CD上，OB＝OD，AB＝CD，∠OBA＝∠D；
(1)求证：△ABO≌△CDO；
(2)当AO∥CD，∠BOD＝30°，求∠A的度数．
23．(8分)已知a+b＝5，ab＝3．
(1)求a2b+ab2的值；
(2)求a2+b2的值．
五、解答题(三)(本大题共2个小题，每小题10分，共20分)
24．(10分)在△ABC中，∠ACB＝90°，AC＝BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．
(1)当直线MN绕点C旋转到图1位置时，求证：DE＝AD+BE；
(2)当直线MN绕点C旋转到图2位置时，试问：DE，AD，BE有怎样的等量关系？请写出这个等量关系，并加以证明．
(3)当直线MN绕点C旋转到图3位置时，DE，AD，BE之间的等量关系是 (直接写出答案，不需证明．)
25．(10分)如图，在△ABC中，∠BAD＝∠DAC，DF⊥AB，DM⊥AC，AF＝10厘米，AC＝14厘米，动点E以4厘米/秒的速度从A点向F点运动，动点G以2厘米/秒的速度从C点向A点运动，当一个点到达终点时，另一个点随之停止运动，设运动时间为t秒．
(1)求证：AF＝AM；
(2)求证：在运动过程中，不管t取何值，都有S△AED＝2S△DGC；
(3)当t取何值时，△DFE与△DMG全等．
2023-2024学年广东省东莞市八年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本大题共10个小题，每小题3分，共30分)
1．【解答】解：由题意知，这样设计蕴含的数学依据是三角形具有稳定性，
故选：D．
2．【解答】解：A．∵5+5＜11，∴5，5，11不能组成三角形，不符合题意；
B．∵7+8＝15，∴7，8，15不能组成三角形，不符合题意；
C．∵2+4＜7，∴7，2，4不能组成三角形，不符合题意；
D．∵13+12＞20，∴13，12，20能组成三角形，正确，符合题意．
故选：D．
3．【解答】解：A．a2与a不是同类项不能合并，该选项不符合题意；
B．a2⋅a3＝a5，故该选项不正确，不符合题意；
C． (a2)3＝a6，故该选项正确，符合题意；
D．a9÷a3＝a6，故该选项不正确，不符合题意；
故选：C．
4．【解答】解：A．6a2b2＝3ab•2ab，等式的左边不是一个多项式，不属于因式分解，故本选项不符合题意；
B．(x+1)(x﹣1)＝x2﹣1，从等式的左边到右边的变形属于整式乘法，不属于因式分解，故本选项不符合题意；
C．x2﹣4x+4＝(x﹣2)2，由左边到右边的变形属于因式分解，故本选项符合题意；
D．x2-x-4＝x(x﹣1)﹣2，不是把一个多项式化成几个整式的积的形式，不属于因式分解，故本选项不符合题意．
故选：C．
5．【解答】解：多边形的边数是：，即该多边形是八边形．
故选：C．
6．【解答】解：
∵△ABC和△DEF全等，AC＝DF＝b，DE＝AB＝a，
∴∠1＝∠B，∠A＝∠D＝50°，∠F＝∠C＝72°，
∴∠1＝180°﹣∠D﹣∠F＝58°，
故选：B．
7．【解答】解：A、添加CB＝CD，根据SSS，能判定△ABC≌△ADC，
故A选项不符合题意；
B、添加∠BCA＝∠DCA时，不能判定△ABC≌△ADC，
故B选项符合题意；
C、添加∠BAC＝∠DAC，根据SAS，能判定△ABC≌△ADC，
故C选项不符合题意；
D、添加∠B＝∠D＝90°，根据HL，能判定△ABC≌△ADC，
故D选项不符合题意；
故选：B．
8．【解答】解：①若∠A+∠B＝∠C，因为∠A+∠B+∠C＝180°，
所以2∠C＝180°，即∠C＝90°，
所以△ABC是直角三角形，符合题意；
②若∠A：∠B：∠C＝1：2：3，则，
所以△ABC是直角三角形，符合题意；
③若∠A＝∠B＝∠C，则∠A＝∠B＝∠C＝60°，
所以△ABC不是直角三角形，不符合题意；
④若∠A＝90°﹣∠B，则∠A+∠B＝90°，所以∠C＝90°，
所以△ABC是直角三角形，符合题意，
综上，能确定△ABC是直角三角形的有①②④．
故选：B．
9．【解答】解：∵(m﹣n)(﹣m﹣n)＝﹣(m﹣n)(m+n)＝﹣(m2﹣n2)，
∴选项A不符合题意；
∵(﹣1+mn)(1+mn)＝(mn)2﹣12，
∴选项B不符合题意；
∵(﹣x+y)(x﹣y)＝﹣(x﹣y)2，
∴选项C符合题意；
∵(2a﹣b)(2a+b)＝(2a)2﹣b2，
∴选项D不符合题意；
故选：C．
10．【解答】解：∵A1B是∠ABC的平分线，A1C是∠ACD的平分线，
∴∠A1BC=∠ABC，∠A1CD=∠ACD，
又∠A1CD＝∠A1+∠A1BC，∠ACD＝∠A+∠ABC，
∴∠A1BC=(∠A+∠ABC)，
∴∠ABC+∠A1=(∠A+∠ABC)，
∴∠A1=∠A，
∵∠A＝a，
∴∠A1=，
同理可得：∠A2=∠A1=·=，
∴∠An=，
∴∠A2023=．
故选：C．
二、填空题(本大题共7小题，每小题4分，共28分)
11．【解答】解：2mn﹣6m＝2m(n﹣3)．
故答案为：2m(n﹣3)．
12．【解答】解：设第三边长为x，
∵两边长分别是2和3，
∴3﹣2＜x＜3+2，
即：1＜x＜5，
∵第三边长为奇数，
∴x＝3，
∴这个三角形的周长为2+3+3＝8，
故答案为：8．
13．【解答】解：∵AE是△ABC的边BC上的中线，
∴CE＝BE，
∵△ACE的周长比△AEB的周长多1，
∴(AC+AE+CE)﹣(AB+BE+AE)＝1，即AC﹣AB＝1，
∵AC＝6，
∴AB＝5，
故答案为：5．
14．【解答】解：如图所示：∠2＝45°，
在△ACB和△DCE中，
，
∴△ACB≌Rt△DCE(SAS)，
∴∠ABE＝∠3，
∴∠1+∠2+∠3＝(∠1+∠3)+45°＝90°+45°＝135°．
故答案为：135．
15．【解答】解：∵am•an＝am+n，
∴am+n＝am•an＝3×2＝6．
16．【解答】解：过点D作DE⊥AB于点E，如图所示：
∵∠C＝90°，AD平分∠BAC，CD＝5，
∴DE＝DC＝5，
∵AB＝16，
∴S△ABD=AB·DE=40．
故答案为：40．
17．【解答】解：设正方形 A，B 的边长分别为a，b，则图甲中阴影部分面积为
，
图乙中阴影部分面积为，
∴，
∴，
∴．
故答案为：3．
三、解答题(一)(本大题共3个小题，每小题6分，共18分)
18．【解答】解：(1)(2x﹣1)(3x+4)
＝6x2+8x﹣3x﹣4
＝6x2+5x﹣4；
(2)
．
19．【解答】证明：∵BF＝CE，
∴BC＝EF，
∵AB⊥BE，DE⊥EF，
∴∠B＝∠E＝90°，
在Rt△ABC和Rt△DEF中，
，
∴Rt△ABC≌Rt△DEF(HL)．
20．【解答】解：(1)如图所示．
(2)∵BE平分∠ABC，∠ABF＝35°，
∴FBD＝ABF＝35°．
∵AD是BC边上的高，
∴AD⊥BC，
∴∠BDF＝90°，
∴∠AFB＝∠BDF+∠FBD＝90°+35°＝125°．
四、解答题(二)(本大题共3个小题，每小题8分，共24分)
21．【解答】解：(4x3﹣6x2y+4x2)÷(﹣2x)2
＝(4x3﹣6x2y+4x2)÷4x2
＝x﹣y+1，
当x＝3，y＝﹣2时，原式＝3﹣×(﹣2)+1
＝3+3+1
＝7．
22．【解答】(1)证明：在△ABO和△CDO中，
，
∴△ABO≌△CDO(SAS)；
(2)解：∵△ABO≌△CDO，
∴∠AOB＝∠COD，∠A＝∠C，
∴∠AOB﹣∠COB＝∠COD﹣∠COB，
∴∠AOC＝∠BOD＝30°，
∵OA∥CD，
∴∠C＝∠AOC＝30°，
∴∠A＝30°．
23．【解答】解：(1)∵a+b＝5，ab＝3，
∴原式＝ab(a+b)
＝3×5
＝15；
(2)∵a+b＝5，ab＝3，
∴原式＝(a+b)2﹣2ab
＝52﹣2×3
＝25﹣6
＝19．
五、解答题(三)(本大题共2个小题，每小题10分，共20分)
24．【解答】解：(1)∵在Rt△ABC中，∠BCA＝90°，∠ADC＝∠BEC＝90°
∴∠ACD+∠BCE＝90°，∠BCE+CBE＝90°
∴∠ACD＝∠CBE
∵AB＝AC
∴△ADC≌△CEB(AAS)
∴AD＝CE，BE＝CD
∴DE＝DC+CE＝BE+AD．
(2)结论：AD＝BE+DE．理由如下：
∵AD⊥MN，BE⊥MN，
∴∠ADC＝∠BEC＝90°，
∴∠ACD+∠BCD＝90°，∠BCD+∠CBE＝90°，
∴∠ACD＝∠CBE，
在△ABD和△ACE中
，
∴△ACD≌△CBE(AAS)，
∴AD＝CE，CD＝BE，
∵AD＝CD+DE＝BE+DE，
(3)结论：BE＝AD+DE．
理由：易证△ACD≌△CBE，
∴BE＝CD，AD＝CE，
∴BE＝CE+DE＝AD+DE．
故答案为BE＝AD+DE．
25．【解答】(1)证明：∵∠BAD＝∠DAC，DF⊥AB，DM⊥AC，
∴DF＝DM，
在Rt△AFD和Rt△AMD中，
，
∴Rt△AFD≌Rt△AMD(HL)；
∴AF＝AM；
(2)证明：∵∠BAD＝∠DAC，DF⊥AB，DM⊥AC，
∴DF＝DM，
∵S△AED＝AE•DF，S△DGC＝CG•DM，
∴，
∵点E以2cm/s的速度从A点向F点运动，
动点G以1cm/s的速度从C点向A点运动，
∴AE＝4t(cm)，CG＝2t(cm)，
∴＝2，
即，
∴在运动过程中，不管t取何值，都有S△AED＝2S△DGC．
(3)解：若△DFE与△DMG全等，且DF＝DM，∠EFD＝∠GMD＝90°，
∴EF＝MG，
①当0＜t＜2时，点G在线段CM上，点E在线段AF上，
∴EF＝10﹣4t，MG＝4﹣2t，
∴10﹣4t＝4﹣2t，
∴t＝3(不合题意，舍去)；
②当2≤t＜2.5时，点G在线段AM上，点E在线段AF上，
EF＝10﹣4t，MG＝2t﹣4，
∴10﹣4t＝2t﹣4，
∴t＝；
综上所述，当t＝秒时，△DFE与△DMG全等。