



青岛版九年级上册2.1 锐角三角比课堂教学课件ppt
展开经历实验、观察、探究、交流、猜测等数学活动,探索锐角三角比的意义,丰富基本的数学活动经验.
了解直角三角形中锐角的正弦、余弦、正切的概念,认识锐角三角比sinA,csA,tanA的符号,发展符号意识.
已知直角三角形的两条边,会求直角三角形锐角的三角比.
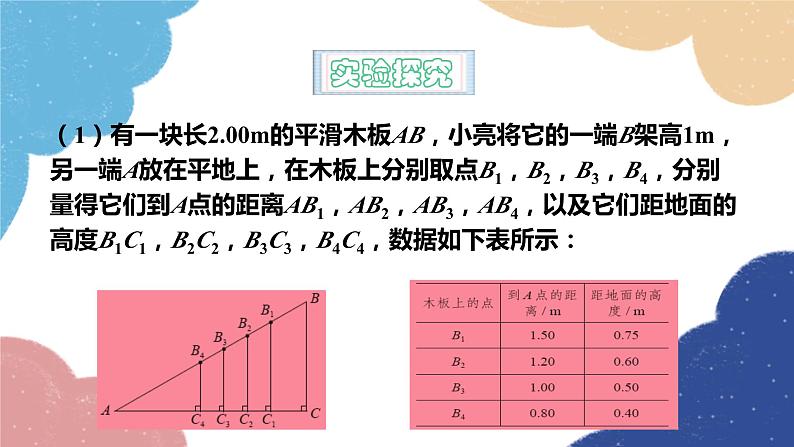
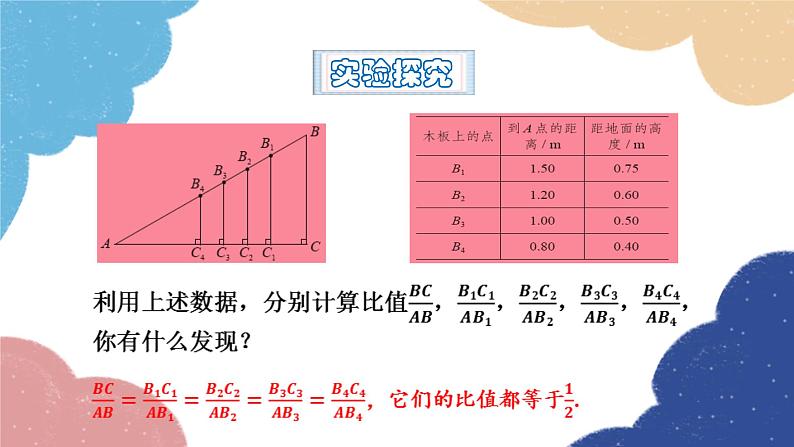
(1)有一块长2.00m的平滑木板AB,小亮将它的一端B架高1m,另一端A放在平地上,在木板上分别取点B1,B2,B3,B4,分别量得它们到A点的距离AB1,AB2,AB3,AB4,以及它们距地面的高度B1C1,B2C2,B3C3,B4C4,数据如下表所示:
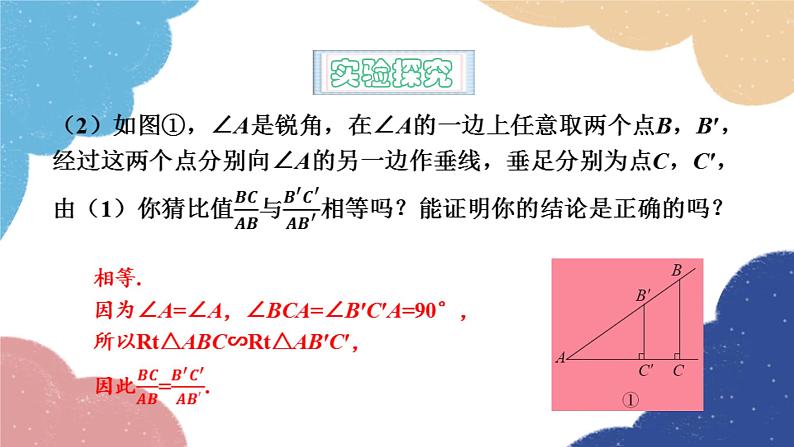
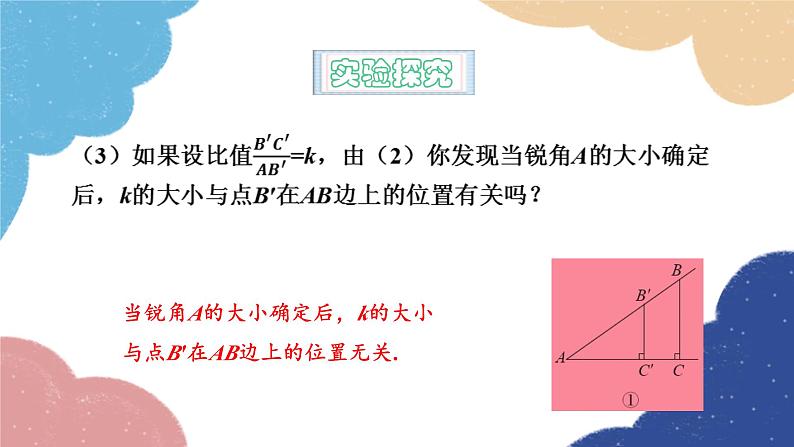
当锐角A的大小确定后,k的大小与点B′在AB边上的位置无关.
对于确定的锐角A来说,比值k与点B′在AB边上的位置无关,只与锐角A的大小有关.
我们把锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即
我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作csA,即
我们把锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即
锐角A的正弦、余弦、正切统称锐角A的三角比.
在下图中,把∠A的对边记作a,∠B的对边记作b,∠C的对边记作c,你能分别用a,b,c表示∠A和∠B的正弦、余弦和正切吗?
【注意】sinA,csA,tanA分别是一个完整的记号.当角只用一个大写字母或小写字母表示时,习惯上在记号中省去角的符号“∠”,不能理解成sin·A,cs·A,tan·A.
如图,在Rt△ABC中,∠C=90°,a=2,b=4.求∠A的正弦、余弦、正切的值.
在Rt△ABC中,∠A为锐角
3.如果Rt△ABC∽Rt△A′B′C′,∠C=∠C′=90°,sinA等于sinA′吗?为什么?csA与csA′呢?
解:sinA=sinA′,csA=csA′.理由:因为Rt△ABC∽Rt△A′B′C′,所以∠A=∠A′,所以sinA=sinA′,csA=csA′.
青岛版九年级上册第2章 解直角三角形2.1 锐角三角比优质课课件ppt: 这是一份青岛版九年级上册<a href="/sx/tb_c99057_t3/?tag_id=26" target="_blank">第2章 解直角三角形2.1 锐角三角比优质课课件ppt</a>,共27页。PPT课件主要包含了比萨斜塔,课堂导入,知识回顾,问题一,问题2,问题3,设参法,问题4,测量计算,推理证明等内容,欢迎下载使用。
九年级上册2.3 用计算器求锐角三角比备课ppt课件: 这是一份九年级上册2.3 用计算器求锐角三角比备课ppt课件,共24页。PPT课件主要包含了学习目标,问题引入,动手操作,sin30°,注意事项,典例训练,挑战自我,问题思考,课堂小结等内容,欢迎下载使用。
青岛版九年级上册2.3 用计算器求锐角三角比教课内容ppt课件: 这是一份青岛版九年级上册2.3 用计算器求锐角三角比教课内容ppt课件,共37页。PPT课件主要包含了2sin9°,≈09659,≈08121,≈15926,≈09686,≈08071,≈05012,≈09999,≈30781,习题23等内容,欢迎下载使用。













