数学九年级上册第2章 解直角三角形2.5 解直角三角形的应用评课课件ppt

这是一份数学九年级上册第2章 解直角三角形2.5 解直角三角形的应用评课课件ppt，共17页。PPT课件主要包含了学习目标，情境引入，概念引入，ih∶l，典例探究，概括总结，方法技巧，当堂检测等内容，欢迎下载使用。

了解测量名词“坡度”“坡角”的意义，能根据题意及测量术语绘出示意图.
会用解直角三角形的有关知识解某些简单的实际问题.
认识数学与生产活动的联系，培养数学的应用意识，感悟抽象、转化和数形结合等数学思想.
在修路、筑坝、开渠和挖河时，都会遇到修筑斜坡的问题.
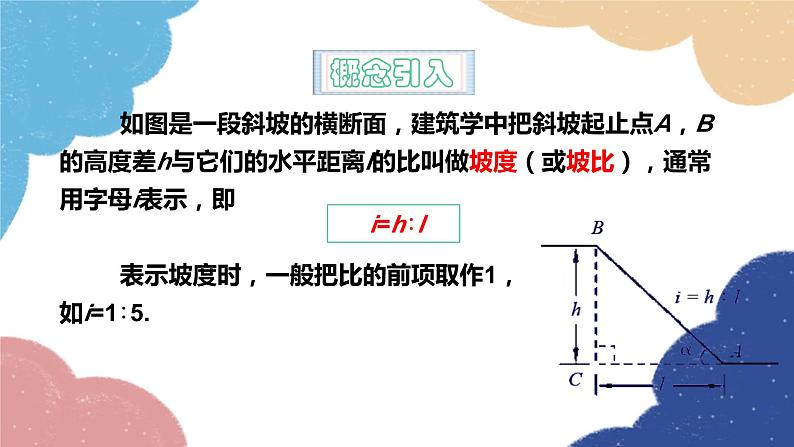
如图是一段斜坡的横断面，建筑学中把斜坡起止点A，B的高度差h与它们的水平距离l的比叫做坡度（或坡比），通常用字母i表示，即 表示坡度时，一般把比的前项取作1，如i=1∶5.
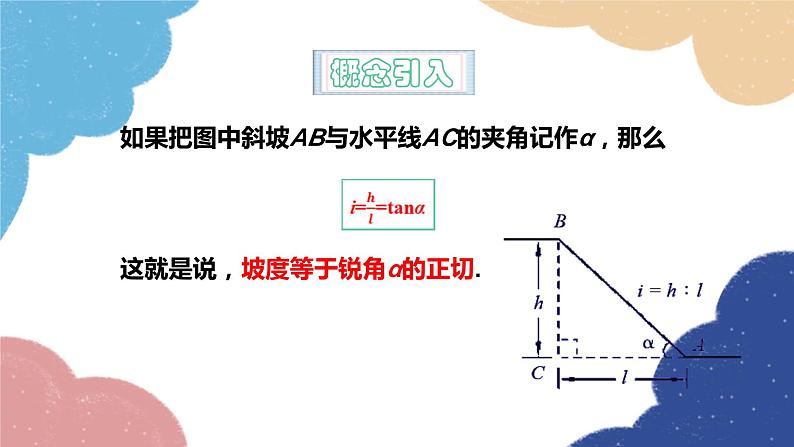
如果把图中斜坡AB与水平线AC的夹角记作α，那么 这就是说，坡度等于锐角α的正切.
某地计划在河流的上游修建一条拦水大坝.大坝的横断面ABCD是梯形，坝顶宽BC=6m，坝高25m，迎水坡AB的坡度i=1∶3，背水坡CD的坡度i=1∶2.5.（1）求斜坡AB和CD的长（精确到0.01m）；
（2）AD=AE+EF+FD=75+6+62.5=143.5（m）.所以，斜坡AB的长约为79.06m，CD的长约为67.31m；水坝的底面宽AD为143.5m.
某地计划在河流的上游修建一条拦水大坝.大坝的横断面ABCD是梯形，坝顶宽BC=6m，坝高25m，迎水坡AB的坡度i=1∶3，背水坡CD的坡度i=1∶2.5.（2）求拦水大坝的底面AD的宽.
有关坡度问题常过斜坡的顶点作垂线构造以斜坡为斜边的直角三角形.如本例题通过作出两条高，把梯形转化为两个直角三角形和一个矩形来求解.
坡度问题中构造直角三角形的常用方法
如图，要测量铁塔的高AB，在地面上选取一点C，在A，C两点间选取一点D，测得CD=14m，在C，D两点处分别用测角仪测得铁塔顶端B的仰角为α=30°和β=45°.测角仪支架的高为1.2m，求铁塔的高（精确到0.1m）.
α，β分别在两个直角三角形中，怎么办？
A1B是两个直角三角形公共的直角边，C1D1是直角边A1C1与A1D1的差.可以利用方程解决这个问题.
此类问题中常涉及两个直角三角形，常将实际问题转化为解直角三角形问题.在利用锐角三角比解直角三角形时，不能直接求得结果的，常引入未知数构造方程求解.
1.如图，为了测量山坡护坡石坝的坡度（坡面的铅直高度与水平宽度的比称为坡度），把一根长5m的竹竿AC斜靠在石坝旁，量出杆长1m处的D点离地面的高度DE=0.6m，又量得杆底与坝脚的距离AB=3m，则石坝的坡度为_____.