青岛版九年级上册3.4 直线与圆的位置关系授课课件ppt

这是一份青岛版九年级上册3.4 直线与圆的位置关系授课课件ppt，共14页。PPT课件主要包含了学习目标，知识回顾，d＞r，d＝r，d＜r，新知探究，新知精讲，典例精讲，课堂小结，直线l与⊙O相交等内容，欢迎下载使用。

了解直线与圆的位置关系，掌握切线的概念；
能根据公共点的个数或圆心到直线的距离与 圆的半径的关系判定直线与圆的位置关系， 感悟分类的数学思想.
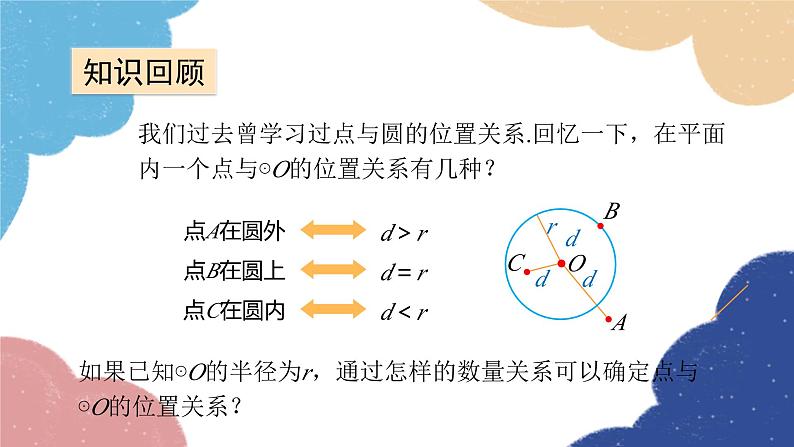
我们过去曾学习过点与圆的位置关系.回忆一下，在平面内一个点与⊙O的位置关系有几种？
如果已知⊙O的半径为r，通过怎样的数量关系可以确定点与⊙O的位置关系？
点A在圆外点B在圆上 点C在圆内
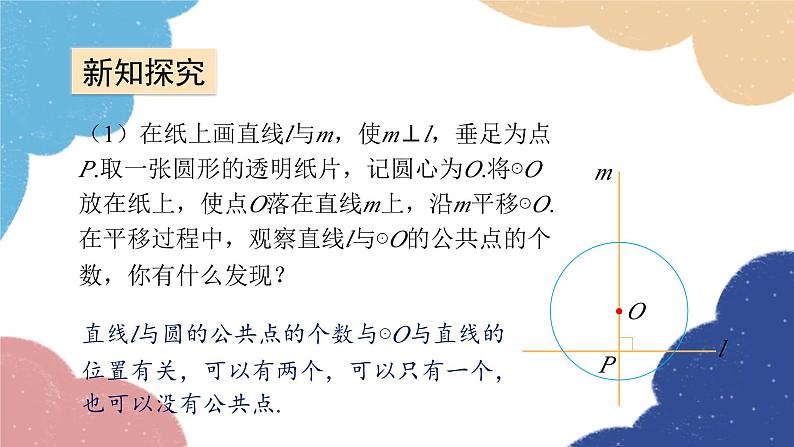
（1）在纸上画直线l与m，使m⊥l，垂足为点P.取一张圆形的透明纸片，记圆心为O.将⊙O放在纸上，使点O落在直线m上，沿m平移⊙O.在平移过程中，观察直线l与⊙O的公共点的个数，你有什么发现？
直线l与圆的公共点的个数与⊙O与直线的位置有关，可以有两个，可以只有一个，也可以没有公共点.
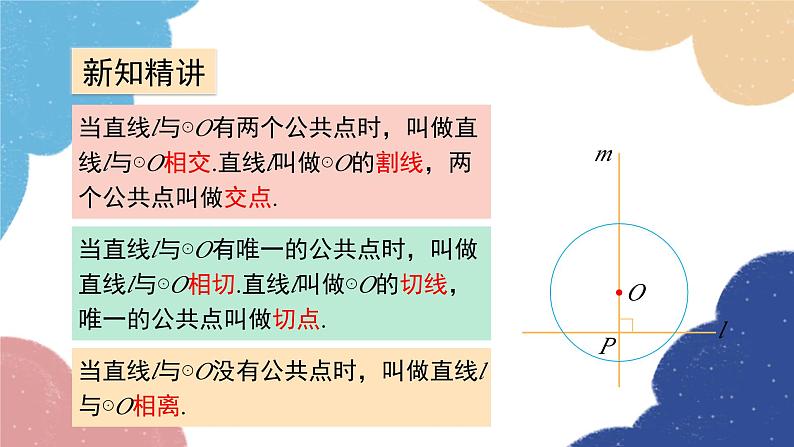
当直线l与⊙O有两个公共点时，叫做直线l与⊙O相交.直线l叫做⊙O的割线，两个公共点叫做交点.
当直线l与⊙O没有公共点时，叫做直线l与⊙O相离.
当直线l与⊙O有唯一的公共点时，叫做直线l与⊙O相切.直线l叫做⊙O的切线，唯一的公共点叫做切点.
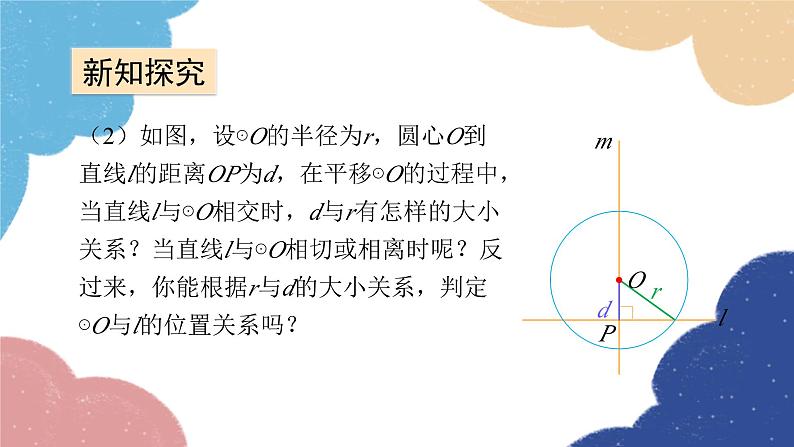
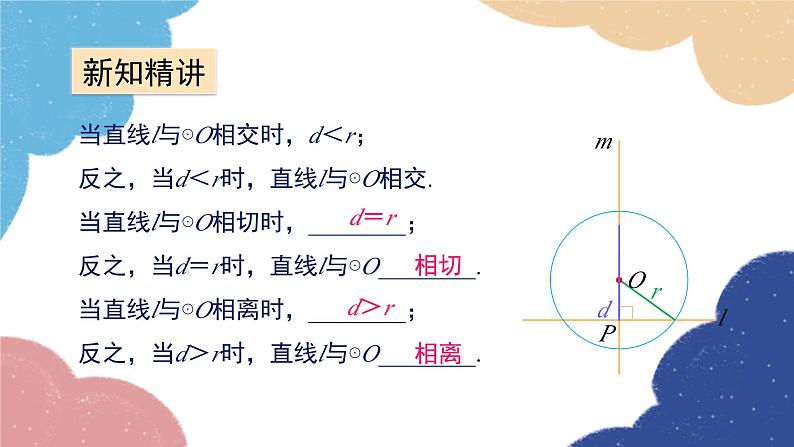
（2）如图，设⊙O的半径为r，圆心O到直线l的距离OP为d，在平移⊙O的过程中，当直线l与⊙O相交时，d与r有怎样的大小关系？当直线l与⊙O相切或相离时呢？反过来，你能根据r与d的大小关系，判定⊙O与l的位置关系吗？
当直线l与⊙O相交时，d＜r；反之，当d＜r时，直线l与⊙O相交.当直线l与⊙O相切时，________；反之，当d＝r时，直线l与⊙O________.当直线l与⊙O相离时，________；反之，当d＞r时，直线l与⊙O________.
例1 在Rt△ABC中，∠C＝90°，AC＝3 cm，BC＝4 cm.以点C为圆心，r为半径画圆.当r分别取下列各值时，斜边AB所在的直线与⊙C具有怎样的位置关系？（1）r＝2 cm；（2）r＝2.4 cm；（3）r＝3 cm.
即圆心C到AB的距离d＝2.4 cm.（1）当r＝2 cm时，d＞r，直线AB与⊙C相离；（2）当r＝2.4 cm时，d＝r，直线AB与⊙C相切；（3）当r＝3 cm时，d＜r，直线AB与⊙C相交.
当直线l与⊙O有______公共点时，叫做直线l与⊙O相交.直线l叫做⊙O的______，两个公共点叫做______.
当直线l与⊙O______公共点时，叫做直线l与⊙O相离.
当直线l与⊙O有________公共点时，叫做直线l与⊙O相切.直线l叫做⊙O的______，唯一的公共点叫做______.
r与d的大小关系与⊙O与l的位置关系
1.已知⊙A的直径为6，点A的坐标为（-3，-4），则⊙A与x轴的位置关系是______，⊙A与y轴的位置关系是______.
2.如图，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为（-3，0），将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为_______.
3.如图，已知⊙O是以数轴的原点为圆心，半径为1的圆，∠AOB＝45°，点P在数轴上运动，若过点P且与OA平行（或重合）的直线l与⊙O有公共点，设点P在数轴上对应的数值为a，则a的取值范围是_______________.