数学九年级上册4.6 一元二次方程根与系数的关系背景图课件ppt

这是一份数学九年级上册4.6 一元二次方程根与系数的关系背景图课件ppt，共19页。PPT课件主要包含了学习目标，合作探究，新知讲解，新知巩固，例题解答，规律总结，随堂练习等内容，欢迎下载使用。

(1)解下面的一元二次方程，并填写结果：①x2+3x+2=0, x1=_________,x2=_________.②x2-5x+6=0, x1=_________,x2=_________.③3x2+x-2=0, x1=_________,x2=__________.④2x2-4x+1=0. x1=_________,x2=__________.
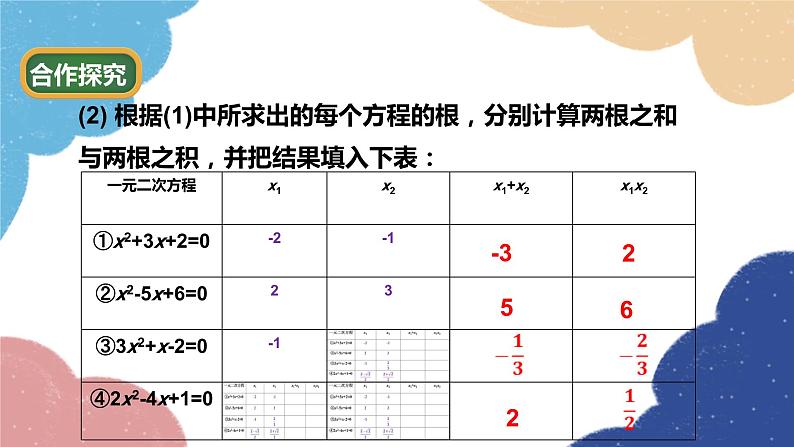
(2) 根据(1)中所求出的每个方程的根，分别计算两根之和 与两根之积，并把结果填入下表：
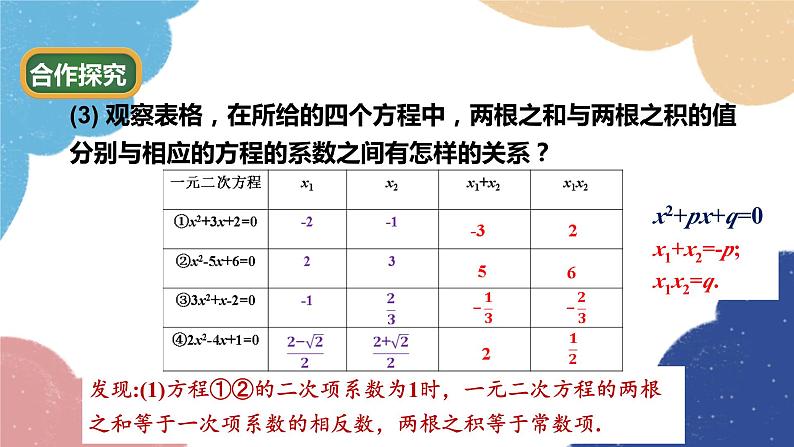
发现:(1)方程①②的二次项系数为1时，一元二次方程的两根之和等于一次项系数的相反数，两根之积等于常数项.
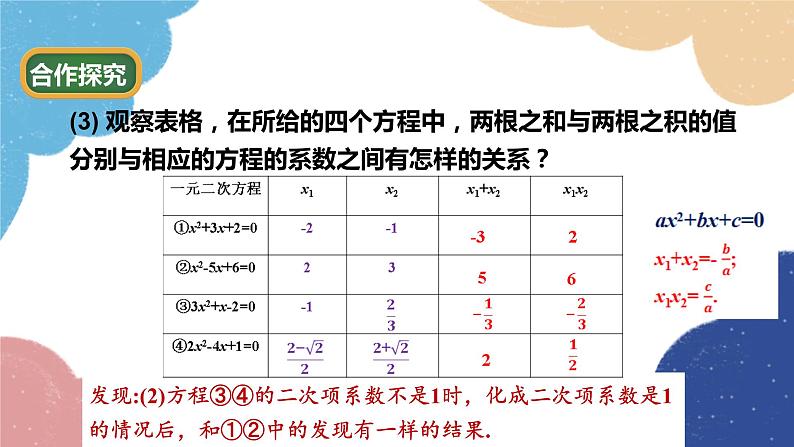
(3) 观察表格，在所给的四个方程中，两根之和与两根之积的值分别与相应的方程的系数之间有怎样的关系？
x2+px+q=0x1+x2=-p;x1x2=q.
发现:(2)方程③④的二次项系数不是1时，化成二次项系数是1的情况后，和①②中的发现有一样的结果.
(4) 由此你猜想一元二次方程ax2+bx+c=0的两个根x1,x2与方程的系数a,b,c之间有什么关系？尝试证明你的猜想是正确的.
一元二次方程的根与系数有以下关系：
如果一元二次方程ax2+bx+c=0的两个根是x1,x2,那么
不解方程，写出下列一元二次方程两个根的和与积.
1. x2 - 2x - 1=0；
2. 2x2 - 6x =0；
3. 3x2 = 4；
4. 3x2-2x=2.
解：x1+x2=2; x1x2=-1；
解：x1+x2=3; x1x2=0；
【例1】关于x的方程3x2+mx-4=0有一个根是2，求另一个根及m的值.
对于例1，还有其他的解法吗？
巧用根与系数的关系，求特殊代数式的值
(1)计算：计算出x1+x2,x1x2的值；(2)变形：将所求的代数式变形为用x1+x2,x1x2表示的式子；(3)代入：代入所求的代数式计算.
1.以3和-1为两根的一元二次方程是（　 　）A．x2+2x-3=0 B．x2+2x+3=0C．x2-2x-3=0 D．x2-2x+3=0
3.关于x的一元二次方程x2-kx-7=0的一个根为x1=1，另一根为x2，则有( ) A．k=-6，x2=-7 B．k=6，x2=-7 C．k=-6，x2=7 D．k=6，x2=7
【解析】由根与系数的关系，得x1+x2 =-7， x1x2=-8，
5.已知关于x的方程方程x2-（k+1）x+（k-2）=0，根据下列条件分别求出k的值：(1) 两根互为相反数; (2)两根互为倒数.
解：Δ=b2-4ac=[-(k+1)]2-4×1×(k-2)=k2-2k+9=(k-1)2+8≥8.
(1)设方程的两根为x1，x2.∵两根互为相反数，∴x1+x2=k+1=0，解得k=-1.
(2)∵两根互为倒数，∴x1x2=k-2=1，解得k=3.