初中数学青岛版八年级上册5.6 几何证明举例图文ppt课件

这是一份初中数学青岛版八年级上册5.6 几何证明举例图文ppt课件，共16页。PPT课件主要包含了教学目标，新知导入，探究新知，课堂练习，课堂小结等内容，欢迎下载使用。
1.掌握并证明线段垂直平分线的性质定理与判定定理；
2.掌握基本的证明方法，会通过分析的方法探索证明的思路
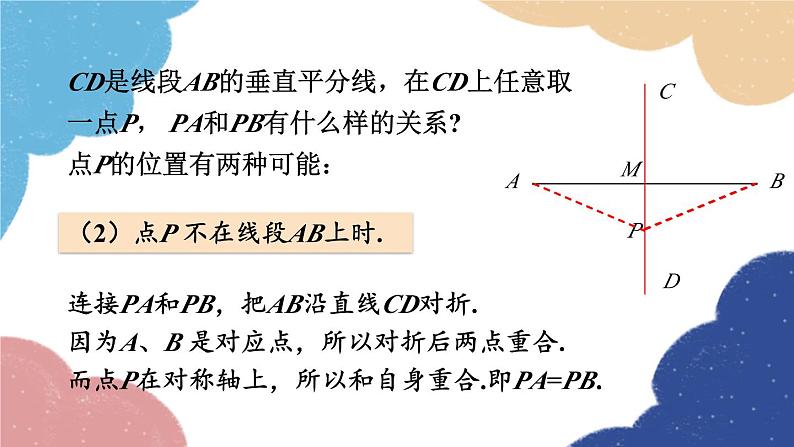
CD是线段AB的垂直平分线，在CD上任意取一点P， PA和PB有什么样的关系?点P的位置有两种可能：
（1）点P 恰是CD和线段AB的交点时.
此时点P与点M重合,所以PA=PB.
（2）点P 不在线段AB上时.
连接PA和PB，把AB沿直线CD对折.因为A、B 是对应点，所以对折后两点重合.而点P在对称轴上，所以和自身重合.即PA=PB.
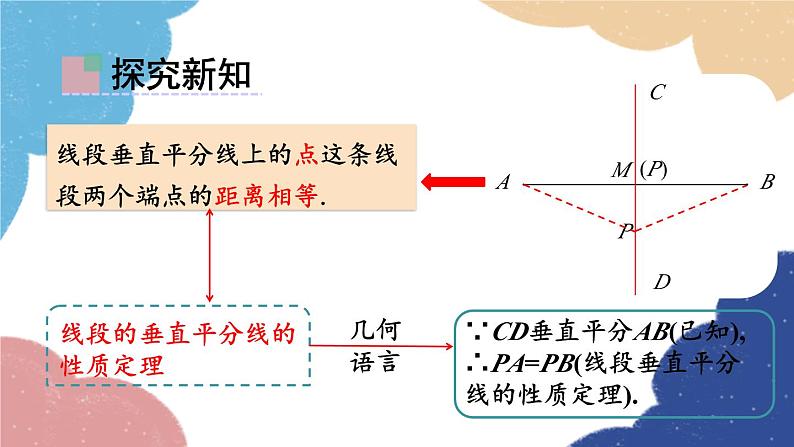
线段垂直平分线上的点这条线段两个端点的距离相等.
线段的垂直平分线的性质定理
∵CD垂直平分AB(已知),∴PA=PB(线段垂直平分线的性质定理).
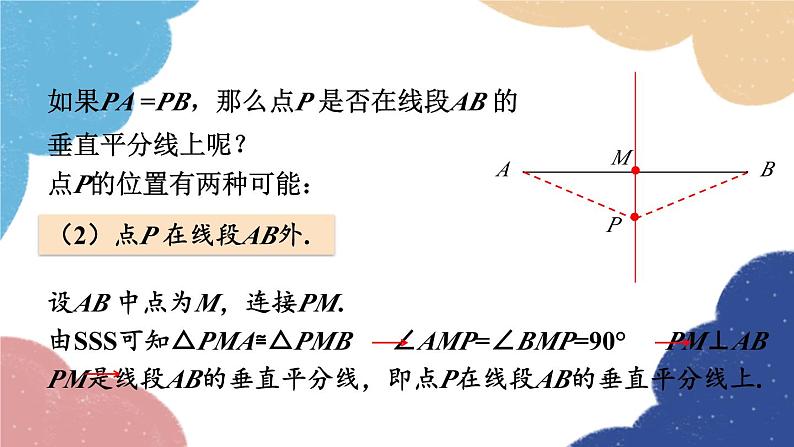
如果PA =PB，那么点P 是否在线段AB 的 垂直平分线上呢？点P的位置有两种可能：
（1）点P 在线段AB上.
点P是AB的中点，此时点P在线段AB的垂直平分线上.
（2）点P 在线段AB外.
设AB 中点为M，连接PM.由SSS可知△PMA≌△PMB ∠AMP=∠BMP=90° PM⊥AB PM是线段AB的垂直平分线，即点P在线段AB的垂直平分线上.
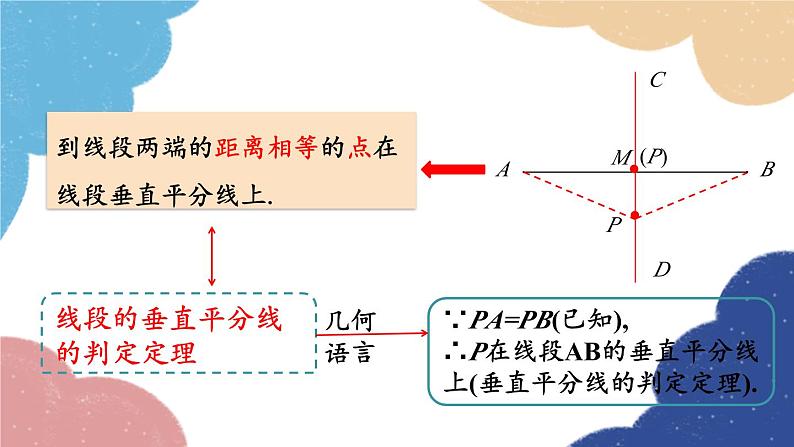
到线段两端的距离相等的点在线段垂直平分线上.
线段的垂直平分线的判定定理
∵PA=PB(已知),∴P在线段AB的垂直平分线上(垂直平分线的判定定理).
例1 已知:如图,在ΔABC中,边AB，BC的垂直平分线交于P.求证：PA=PB=PC.
点P在线段BC的垂直平分线上
点P在线段AB的垂直平分线上
证明：∵MN垂直平分AB∴PA=PB.同理 PB=PC.∴PA=PB=PC.
三角形三边垂直平分线交于一点，这一点到三角形三个顶点的距离相等.
例2 已知如图：一辆汽车在直线公路AB上由A向B行驶，M、N分别表示位于公路AB两侧的村庄，
（1）当汽车行驶到什么位置时距村庄M最近？行驶到什么位置时距村庄N最近？
答：如图，当汽车行驶到P1时，距村庄M最近，当汽车行驶到P2时，距村庄N最近.
根据：直线外一点与直线上各点连结的所有线段中，垂线段最短.
（2）当汽车行驶到什么位置时，与村庄M、N的距离相等？
答：如图 ，当汽车行驶到P3时，与村庄M、N的距离相等.
根据：线段的垂直平分线上的点到这条线段两个端点的距离相等.
1.如图，若AC=12，BC=7，AB的垂直平分线交AB于E，交AC于D，求△BCD的周长.
解：∵ED是线段AB的垂直平分线，∴BD=AD，∵ △BCD的周长=BD+DC+BC∴ △BCD的周长=AD+DC+BC
=12+7=19.
2.如图，如果△ACD的周长为18cm，△ABC的周长为28cm， DE是BC的垂直平分线,根据这些条件，你可以求出哪条线段的长?
解：∵△ACD的周长=AD +CD+AC=18cm； △ABC的周长=AB+AC+BC=28cm；
又∵DE是BC的垂直平分线，∴BD=CD，∴AD+CD=AD+BD=AB.
线段垂直平分线上的点与这条线段两个端点的距离相等.
与线段两个端点距离相等的点，在这条线段的垂直平分线上.