





青岛版1.2 怎样判定三角形相似集体备课ppt课件
展开1.通过推理掌握平行线分线段成比例定理及其推论;2.能够利用平行线分线段成比例定理及其推论进行推理与计算.
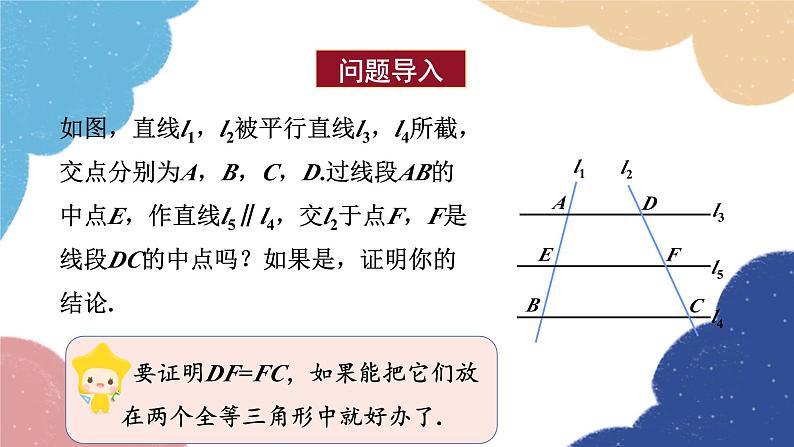
如图,直线l1,l2被平行直线l3,l4所截,交点分别为A,B,C,D.过线段AB的中点E,作直线l5∥l4,交l2于点F,F是线段DC的中点吗?如果是,证明你的结论.
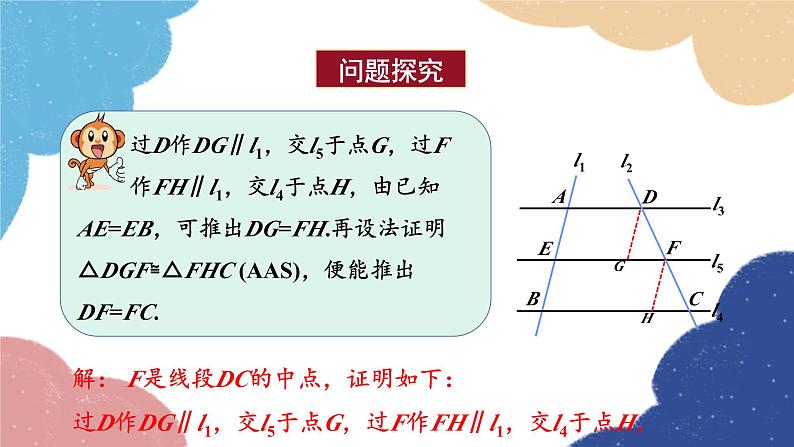
解: F是线段DC的中点,证明如下:过D作DG∥l1,交l5于点G,过F作FH∥l1,交l4于点H,
∵l3∥l4,l5∥l4,∴l3∥l5,∠DFG=∠FCH,∠AEG=∠ABH.又∵DG∥l1,FH∥l1,∴四边形AEGD与四边形EBHF都是平行四边形,∠AEG=∠DGF,∠ABH=∠FHC.∴∠DGF=∠FHC,DG=AE,FH=EB.又∵ AE=EB, ∴DG=FH. ∴△DGF≌△FHC (AAS).∴ DF=FC. 即F是线段DC的中点.
如果l1被l3,l4,l5所截得的线段不相等,上面的结论能进一步推广吗?
思考: (1)如果再取AE的中点P,过点P作直线l6∥l3交l2于点Q(下图①),此时对应线段AP,PB,DQ,QC成比例吗?为什么?
思考: (2)如果取EB的中点P1,过点P1作直线l7∥l3交l2于点Q1 (下图②),此时对应线段AP1,P1B,DQ1,Q1C成比例吗?为什么?
思考: (3)在图①中再继续取AP的中点P2,或的PE的中点P3,或PB的中点P4,或AP4的中点P5,分别过这些点作l3的平行线,重复思考(1)(2)中的推理过程,你能得到什么结论?
思考: (4)一般地,如果任意两条直线l1,l2被一组平行直线l3,l4,l5所截,交点分别是A,B,C;D,E,F.你有什么结论?
思考: (6)特别地,在△ABC中,DE∥BC. ①线段AD,AB,AE, AC成比例吗?②线段AD,AB,DE,BC呢?
在本书中,把下面的命题作为第9个基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
由此,你能得到什么结论?
我们可以得到基本事实9的一个推论:
推论 平行于三角形的一边,并且与其他两边相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.
【例1】如下图,已知直线l1∥l2∥l3, AB = 3 cm, BC = 5 cm,DE = 2.4 cm,求DF的长.
【例2】如图,在△ABC中,E,F分别是AB和AC上的点,且EF∥BC.(1)如果AE=7,EB=5,FC=4.那么AF的长是多少?
(2)如果AB=10,AE=6,AF=5.那么FC的长是多少?
1.如图,已知AB∥CD∥EF,AF交BE于点H,下列结论中错误的是( )
2.如图,ED∥BC,AB=5,AC=7,AD=2,求AE的长.
解:过点A作FH//BC.
∵AB=5, AC=7, AD=2,
∵ ED∥BC,∴ DE//FH//BC.
3.如图所示,如果D,E,F分别在OA,OB,OC上,且DF∥AC,EF∥BC.求证:OD∶OA=OE∶OB
青岛版九年级上册3.1 圆的对称性图文课件ppt: 这是一份青岛版九年级上册3.1 圆的对称性图文课件ppt,共16页。PPT课件主要包含了学习目标,探究圆的轴对称性质,知识回顾,同心圆,点和圆的位置关系,新知探究,新知精讲,一条直线,过圆心,垂直于弦等内容,欢迎下载使用。
初中数学青岛版九年级上册1.4 图形的位似评课课件ppt: 这是一份初中数学青岛版九年级上册1.4 图形的位似评课课件ppt,共20页。PPT课件主要包含了学习目标,情境导入,新知探究,归纳总结,不一定,平行或共线,同一个点,相似比,例题讲解,例题总结等内容,欢迎下载使用。
初中数学青岛版九年级上册第1章 图形的相似1.2 怎样判定三角形相似课前预习ppt课件: 这是一份初中数学青岛版九年级上册第1章 图形的相似1.2 怎样判定三角形相似课前预习ppt课件,共18页。PPT课件主要包含了学习目标,情景导入,陈子测日,新课探究,例题讲解,随堂练习等内容,欢迎下载使用。













