青岛版九年级上册1.2 怎样判定三角形相似课前预习ppt课件

这是一份青岛版九年级上册1.2 怎样判定三角形相似课前预习ppt课件，共16页。PPT课件主要包含了学习目标，温故知新，新知探究，于是便得到，例题讲解，随堂练习，∠ACB等内容，欢迎下载使用。

类比相似多边形的定义，说出相似三角形的定义，经历两个三角形相似条件(两角相等)的探索过程，增强发现问题、提出问题的意识；
掌握“两角分别相等的两个三角形相似”这一定理，并能利用这个定理解决相关的问题.
相似多边形的定义是什么？
两个边数相同的多边形，如果一个多边形的各个角与另一个多边形的各个角对应相等，各边对应成比例，那么这两个多边形叫做相似多边形.
1.相似三角形是最简单、最常见的相似多边形.你能根据相似多边形的定义说出两个怎样的三角形是相似三角形吗？
两个三角形，如果一个三角形的各个角与另一个三角形的各个角对应相等，各边对应成比例，那么这两个三角形叫做相似三角形.
2.回顾判定三角形全等的条件，并思考：怎样判定两个三角形是相似三角形？
我们知道，两个三角形有6对元素，只要其中的3对元素符合下面的一种情况，就可以判定这两个三角形全等.
①两角及其夹边分别相等；②两角及其中一组等角的对边分别相等；③两边及其夹角分别相等；④三边分别相等.
两角相等及其中一边分别相等.
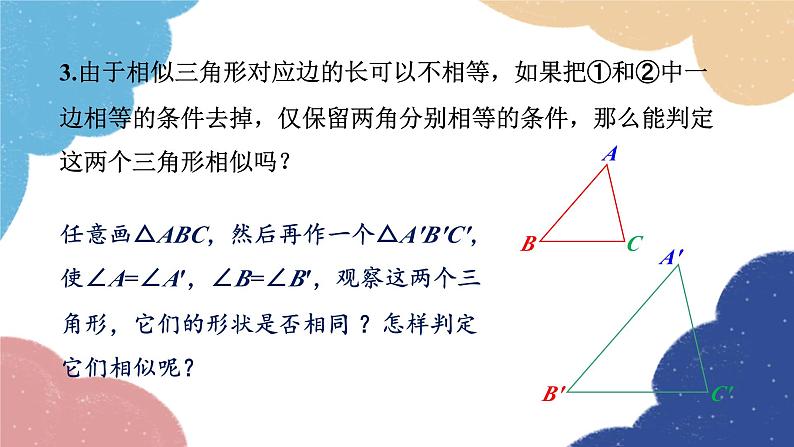
3.由于相似三角形对应边的长可以不相等，如果把①和②中一边相等的条件去掉，仅保留两角分别相等的条件，那么能判定这两个三角形相似吗？
任意画△ABC，然后再作一个△A′B′C′，使∠A=∠A′，∠B=∠B′，观察这两个三角形，它们的形状是否相同 ？怎样判定它们相似呢？
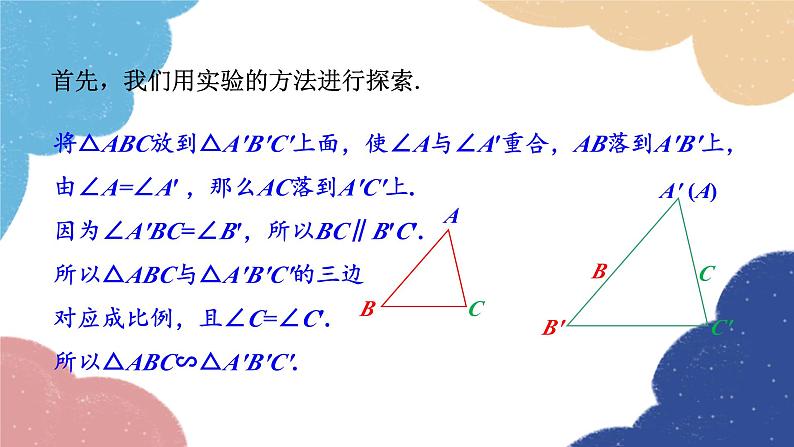
将△ABC放到△A′B′C′上面，使∠A与∠A′重合，AB落到A′B′上，由∠A=∠A′ ，那么AC落到A′C′上.因为∠A′BC=∠B′，所以BC∥B′C′.所以△ABC与△A′B′C′的三边对应成比例，且∠C=∠C′.所以△ABC∽△A′B′C′.
首先，我们用实验的方法进行探索.
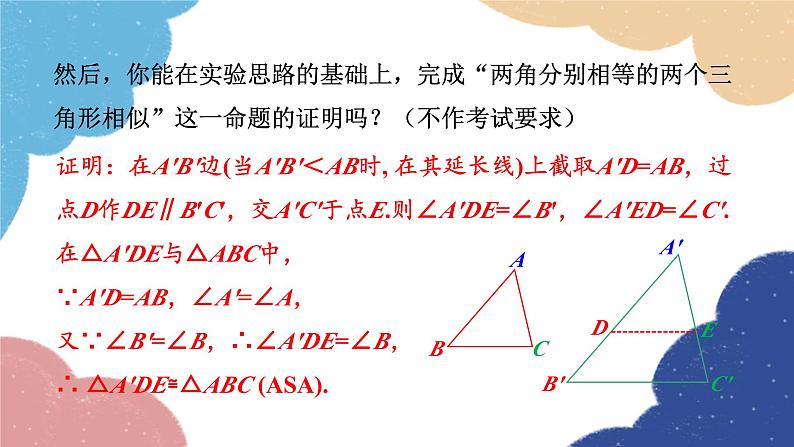
证明：在A′B′边(当A′B′＜AB时, 在其延长线)上截取A′D=AB，过点D作DE∥B′C′，交A′C′于点E.则∠A′DE=∠B′，∠A′ED=∠C′.在△A′DE与△ABC中，∵A′D=AB，∠A′=∠A，又∵∠B′=∠B，∴∠A′DE=∠B，∴ △A′DE≌△ABC (ASA).
然后，你能在实验思路的基础上，完成“两角分别相等的两个三角形相似”这一命题的证明吗？（不作考试要求）
相似三角形的判定定理1 两角分别相等的两个三角形相似.
△ABC与△A′B′C′相似,
用符号表示为__________________.
△ABC∽△A′B′C′
读作______________________.
△ABC相似于△A′B′C′
书写时应注意_______________________________________.
把表示对应顶点的字母写在对应的位置上
【例1】如图，已知点B，D分别是∠A的两边AC，AE上的点，连接BE，CD，相交于点O，如果∠1=∠2，图中有哪几对相似三角形？说明理由.
解：△DOE∽△BOC，△ABE∽△ADC.理由如下：因为∠1=∠2，∠DOE=∠BOC，由判定定理1，所以 △DOE∽△BOC.同理，由∠E=∠C，∠A=∠A，所以 △ABE∽△ADC.
【例2】如图，B，C分别是∠A两边上的任意一点，过点B作BD⊥AC，垂足为点D . 过点C作CE⊥AB，垂足为点E . BD，CE相交于点F.图中共有几对相似三角形？分别是哪几对？
解：图中共有6对相似三角形，分别是：△ABD∽△ACE，△BEF∽△CDF，△AEC∽△FDC，△ABD∽△FBE ，△ABD∽△FCD，△AEC∽△FEB.
1.如图，AB∥CD，AE∥FD，AE，FD分别交BC于点G，H，则图中共有相似三角形（　　）
A.4对 B.5对 C.6对 D.7对
分析：图中共有相似三角形6对：△CEG∽△CDH，△CEG∽△BFH，△CEG∽△BAG，△CDH∽△BFH ，△CDH∽△BAG，△BFH∽△BAG.
2.如图，D是△ABC的边AB上一点，若∠1= ，则△ADC∽△ACB；若∠2= ，则△ADC∽△ACB.
3.如图，D是△ABC的边AB上一点，连接CD，若AD=2，BD=4，∠ACD=∠B，则AC的长为 .
4.如图，在△ABC中，∠BAC=90°，AD⊥BC于点D，(1)请指出图中所有的相似三角形；(2)你能得出AD2=BD·DC吗？