






青岛版九年级上册3.1 圆的对称性教课课件ppt
展开理解圆的中心对称性和旋转不变性以及圆心角的概念;
探索圆心角与其所对弧、弦之间的相互关系,能运用它 们进行有关的推理和计算;
认识弧的度数的概念,了解圆心角的度数与它所对弧的 度数之间的关系.
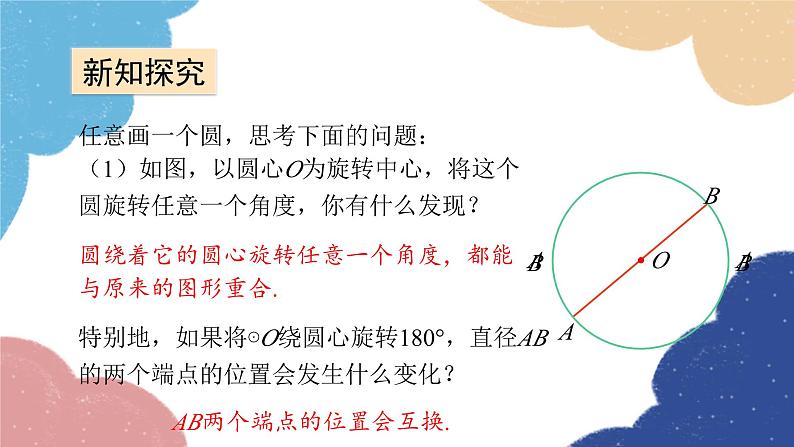
任意画一个圆,思考下面的问题:(1)如图,以圆心O为旋转中心,将这个圆旋转任意一个角度,你有什么发现?
圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.
特别地,如果将⊙O绕圆心旋转180°,直径AB的两个端点的位置会发生什么变化?
AB两个端点的位置会互换.
(2)圆是中心对称图形吗?如果是,哪个点是它的对称中心?
圆是中心对称图形,圆心是它的对称中心.
圆绕着它的圆心旋转180°,能与原来的图形重合.
如图,在⊙O上任取两点C与D,连接OC,OD,得到∠COD.像∠COD这样,顶点在圆心的角叫做圆心角.
(1)如图,任意画一个⊙O,在⊙O内画圆心角∠AOB=∠A′OB′,连接AB,A′B′.
上面的结论在两个等圆中也成立.
定理 在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
这样,就得到下面的定理
例1 如图,AB与DE是⊙O的两条直径,C是⊙O上一点,AC∥DE.求证:(2)BE=EC.
(2)∵∠AOD=∠BOE,∴∠BOE=∠COE.∴BE= CE.
(1)把顶点在圆心的周角等分成360份,每一份圆心角的度数是多少?
(2)把顶点在圆心的周角等分为360份时,整个圆被分成了多少份?每一份的弧是否相等?为什么?
360份,每一份的弧相等,因为每一份的弧所对的圆心角相等.
由此可见,圆心角与它所对的弧有以下关系:
圆心角的度数与它所对弧的度数相等.
圆是中心对称图形,_____是它的对称中心.
____________的角叫做圆心角.
定理 在同圆或______中,如果两个________、两条____、两条____中有一组量相等,那么它们所对应的其余各组量都分别相等.
圆心角的度数与它_____________相等.
1.下列图形中是圆心角的是______.
2.下列说法中正确的是:①圆心角是顶点在圆心的角; ( )②两个圆心角相等,它们所对的弦相等; ( )③在等圆中,圆心角不变,所对的弦也不变.( )
∴∠BOC=∠DOE=∠COD=35°.
∵∠AOE+∠BOC+∠DOE+∠COD=180°,
∴∠AOE=180°-35°-35°-35°=75°.
沪教版 (五四制)九年级下册27.2 圆心角、弧、弦、弦心距之间的关系完整版课件ppt: 这是一份沪教版 (五四制)九年级下册<a href="/sx/tb_c117849_t3/?tag_id=26" target="_blank">27.2 圆心角、弧、弦、弦心距之间的关系完整版课件ppt</a>,文件包含沪教版九年级数学下册272《圆心角弧++弦弦心距之间的关系》第1课时课件pptx、沪教版九年级数学下册272《圆心角弧弦弦心距之间的关系》第2课时课件pptx、沪教版九年级数学下册272《圆心角弧弦弦心距之间的关系》第3课时课件pptx、沪教版九年级数学下册272《圆心角弧弦弦心距之间的关系》分层练习原卷版docx、沪教版九年级数学下册272《圆心角弧弦弦心距之间的关系》分层练习解析版docx等5份课件配套教学资源,其中PPT共63页, 欢迎下载使用。
沪教版 (五四制)九年级下册27.2 圆心角、弧、弦、弦心距之间的关系获奖课件ppt: 这是一份沪教版 (五四制)九年级下册27.2 圆心角、弧、弦、弦心距之间的关系获奖课件ppt,文件包含2723圆心角弧弦弦心距之间的关系课件ppt、272-3圆心角弧弦弦心距之间的关系教案doc等2份课件配套教学资源,其中PPT共8页, 欢迎下载使用。
沪教版 (五四制)九年级下册27.2 圆心角、弧、弦、弦心距之间的关系一等奖课件ppt: 这是一份沪教版 (五四制)九年级下册27.2 圆心角、弧、弦、弦心距之间的关系一等奖课件ppt,文件包含2721圆心角弧弦弦心距之间的关系课件ppt、272-1圆心角弧弦弦心距之间的关系教案doc等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。













