2023-2024学年江苏省泰州市泰兴市九年级上学期期中数学质量检测模拟试题（含答案）

这是一份2023-2024学年江苏省泰州市泰兴市九年级上学期期中数学质量检测模拟试题（含答案），共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
第一部分选择题（共18分）
一、选择题（本大题共6小题，每小题3分，满分18分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，选择正确选项的字母代号涂在答题卡相应的位置上）
1．下列方程是一元二次方程的是（）
A．B．C．D．
2．安老师准备在班上开展“法制”“环保”“安全”三场专题教育讲座，若三场讲座随机安排，则“法制”专题讲座被安排在第一场的概率为（）
A．B．C．D．
3．甲、乙、丙、丁四人各进行了10次射击测试，他们的平均成绩相同，方差分别是，，，．则射击成绩最稳定的是（）
A．甲B．乙C．丙D．丁
4．如图，矩形PAOB内接于扇形OMN，顶点P在上，且不与M，N重合，当点P在上移动时，矩形PAOB的形状、大小随之变化，则的值（）
第4题
A．变大B．变小C．不变D．不能确定
5．刘徽在《九章算术注》中首创“割圆术”，利用圆的内接正多边形来确定圆周率，开创了中国数学发展史上圆周率研究的新纪元．某同学在学习“割圆术”的过程中，作了如图所示的圆内接正八边形．若圆的半径为1，则这个圆内接正八边形的面积为（）
第5题
A．B．C．D．
6．如图，在Rt△ABC中，，，已知B，C在线段DE上，且线段，，则BC的长为（）
第6题
A．6B．C．6.5D．
第二部分非选择题（共132分）
二、填空题（本大题共有10小题，每小题3分，满分30分．请把答案直接填写在答题卡相应位置上）
7、方程的根为______．
8．小敏同学参加市“书香少年”评选，其中综合荣誉分占40%，现场演讲分占60%，已知小敏这两项成绩分别为80分和90分，则小敏的最终成绩为______分．
9．在一个不透明的袋子中装有3个红球和若干个白球．每个球除颜色外其余均相同，若从袋中随机摸出一个球是红球的概率为，则袋中白球的个数为______．
10．若关于x的一元二次方程没有实数根，则k的值可以是______．（写出一个即可）
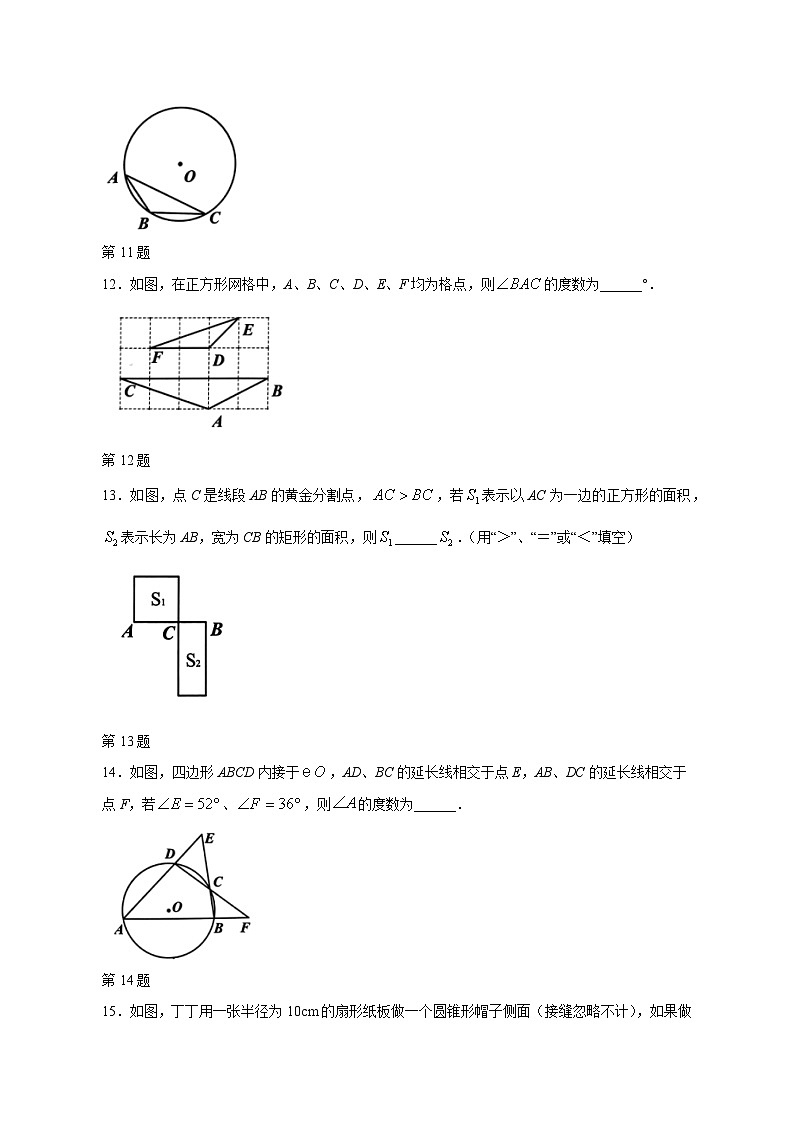
11．如图，是△ABC的外接圆，，，则的半径长等于______．
第11题
12．如图，在正方形网格中，A、B、C、D、E、F均为格点，则的度数为______°．
第12题
13．如图，点C是线段AB的黄金分割点，，若表示以AC为一边的正方形的面积，表示长为AB，宽为CB的矩形的面积，则______．（用“＞”、“＝”或“＜”填空）
第13题
14．如图，四边形ABCD内接于，AD、BC的延长线相交于点E，AB、DC的延长线相交于点F，若、，则的度数为______．
第14题
15．如图，丁丁用一张半径为10cm的扇形纸板做一个圆锥形帽子侧面（接缝忽略不计），如果做成的圆锥形帽子的底面周长为cm，那么这张扇形纸板的面积是______．
第15题
16．如图，矩形ABCD中，，，点E在AD边上，，过点E作交BC于点F．若线段EF上存在3个不同的点P，使得△EDP与△BPF相似，则m的取值范围为______．
第16题
三、解答题（本大题共10小题，满分102分．请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）
17．（本题满分10分）
小明与小华两位同学解一元二次方程的过程如下框：
（1）你认为他们的解法是否正确？直接写出判断结果．
小明的解法_____，小华的解法_____．（填“正确”或者“不正确”）
（2）请你选择合适的方法解一元二次方程．
18．（本题满分8分）
一张圆桌旁设有4个座位，甲先坐在如图所示的座位上，乙、丙、丁三人等可能地坐到其他3个座位上．
（1）乙与甲不相邻而坐的概率为______；
（2）求丙与丁相邻而坐的概率．（画树状图或表格列出所有等可能出现的结果）
19．（本题满分8分）
如图，四边形ABCD是正方形，现有下列几个信息：①E是BC的中点；②﹔③．从以上信息中选择两个作为条件，另一个作为结论，组成一个真命题．
（1）你选择的条件是_____，结论是_____．（填写序号）
（2）证明你构造的命题．
20．（本题满分10分）
已知：平行四边形ABCD的两边AB，AD的长是关于x的方程的两个实数根．
（1）m为何值时，四边形ABCD是菱形？求出这时菱形的边长；
（2）如果AB的长为2，那么平行四边形ABCD的周长是多少？
21．（本题满分10分）
以“徜徉诗词之海，品味文韵之美”为主题的校园传统文化节来了．某校七、八年级开展了“国学朗诵”活动，对学生的活动情况按10分制进行评分，成绩（单位：分）均为不低于6的整数．为了解这次活动的效果，现从这两个年级各随机抽取10名学生的活动成绩作为样本进行整理，并绘制统计图表，部分信息如下：
七年级10名学生活动成绩统计表
八年级10名学生活动成绩扇形统计图
已知七年级10名学生活动成绩的中位数为8.5分．请根据以上信息，完成下列问题：
（1）______，_______；
（2）样本中，八年级活动成绩为7分的学生数是_____，八年级活动成绩的众数为_____分；
（3）若认定比赛成绩不低于9分为“优秀”，根据样本数据，判断本次活动中优秀率高的年级是否平均成绩也高，并说明理由．
22．（本题满分10分）
如图，在方格纸中，点A，B，C都在格点上，用无刻度直尺作图．
（1）在图1中的线段AC上找一个点E，使；
（2）在图2中作一个格点△BDE，使△BDE与△ABC相似，且面积比为．
图1图2
23．（本题满分10分）
小辰同学利用图（1）“光的反射演示器”，直观呈现了光的反射原理．激光笔从左边点C处发出光线，经平面镜点O处反射后，落在右边光屏BE上的点D处（B、C两点均在量角器的边缘上，O为量角器的中心，A、O、B三点共线，，）．他在实验中记录了以下数据：
①水平距离AB的长为96cm；
②铅垂高度AC的长为48cm；
（1）求量角器的半径OB长；
（2）如果小辰想使反射点D沿DB方向下降35cm，求此时激光笔发光点C的铅垂高度AC的长及点A沿OA方向移动的距离．
图1 图2
24．（本题满分10分）
某商店以每件30元的价格购进一批玩具，计划以每件48元的价格销售，为了让顾客得到实惠，现决定降价销售．已知这批玩具销售量y（件）与每件降价x（元）（）之间满足一次函数关系，其图像如图所示．
（1）求y与x之间的函数关系式；
（2）当每件玩具降价2元时，商场获利多少元？
（3）若商场要想获利1680元，且让顾客获得更大实惠，这批玩具每件应降价多少元？
25．（本题满分12分）
如图，在△ABC中，，以AB为直径的交边AC、BC于点D、H，连接BD，过点C作．
（1）用无刻度的直尺和圆规作图：过点B作的切线，交CE于点F（不写作法，保留作图痕迹，标明字母）；
（2）在（1）的条件下，若，，求的直径；
（3）连接AH、OC，AH与OC交点G恰好落在BD上，若AB=40，直接写出弦AD、AH和围成的图形的面积．
26．（本题满分14分）
我们知道，角的内部到角两边距离相等的点在角的平分线上．由此，我们可以引入如下新定义：到三角形的两边距离相等的点，叫做此三角形的准内心．
（1）如图（1），在Rt△ABC中，，，，△ABC的准内心P在△ABC的直角边上，求AP的长．
（2）如图（2），△ABC内接于，BC为直径，点A在BC上方的圆弧上运动，若△ABC的准内心在上，则必有一个准内心P的位置始终不变．
①确定该准内心P的位置（用文字语言叙述）；
②若△ABC中，，，求PC、PA的长；
③设，，求△ABC的面积S（用含m、n的代数式表示）．
图1图2
答案
一、选择题（每题3分，共18分）
二、填空题〔每题3分，共30分）
7．8或－2 8．869．9 10．－1（任一负数即可）11．512．135°13．＝14．46°
15． 16．且
三、解答题〔共102分）
17．（1）不正确，不正确，
（2）解：，，
18．（1）
（2）记左下右为ABC
19．（1）①②；③（答案不唯一）
（2）略
20．（1）
边长为1
（2）
周长为6
21．（1）2；2
（1）2；8分
（3）不是；
七年级的平均分：8.3分，优秀率50%
八年级的平均分：8.4分，优秀率40%
，但
22．
（1）设，在Rt△AOC中，∵
∴∴
（2）∵∴
当，时，；
当时，，
∴，点A移动距离：
24．（1）．
（2）
设降价x元，则，
（3）或
∵让顾客得到实惠∴
25．
（1）以C为圆心，CD为半径画弧交CE于点F，连接BF，BF即为所求（答案不唯一）
（2）∵AB时的直径∴又∵∴
∵，∴﹒
在（1）的条件下证
设，
∵
∴，∴
（3）
26．（1）或
（2）
①该准内心P为下方圆弧的中点
②，
③（证明仅供参考）
【方法一】
过点P作PA的垂线交AC的延长线于点D证明：
得
证明：△APD为等腰直角三角形
得
∴
∴
∴
∴
∴
∴
【方法二】
过点P作AB、AC的垂线段，垂足为点E、D
证明：
得
证明：正方形AEPD
∵
∴
小明：
两边同除以得
．
则．
小华：
移项，得．
提取公因式，得．
则或．
解得，．
成绩/分
6
7
8
9
10
人数
2
1
a
b
3
题号
1
2
3
4
5
6
答案
D
C
A
C
D
B