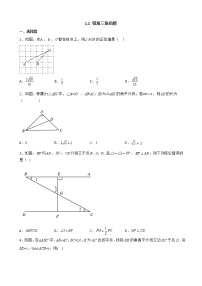
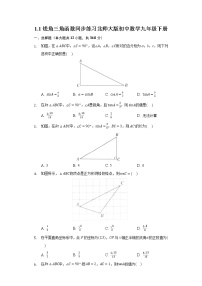
数学北师大版第一章 直角三角形的边角关系1 锐角三角函数优秀习题

这是一份数学北师大版第一章 直角三角形的边角关系1 锐角三角函数优秀习题，共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共12小题，共36分。在每小题列出的选项中，选出符合题目的一项）
1.某人沿着有一定坡度的坡面前进了10米，此时他与水平地面的垂直距离为5米，则这个坡面的坡度为( )
A. 1：2B. 1： 3C. 30°D. 60°
2.如图，在矩形ABCD中，点E是边BC的中点，AE⊥BD，垂足为F，则tan∠BDE的值是
( )
A. 24B. 14C. 13D. 23
3.在如图所示8×8的网格中，小正方形的边长为1，点A、B、C、D都在格点上，AB与CD相交于点E，则∠AED的正切值是
( )
A. 2B. 12C. 23D. 55
4.如图，在4×4的正方形网格中，每个小正方形的边长为1，顶点为格点，若△ABC的顶点均在格点上，则cs∠BAC的值是( )
A. 55B. 105C. 2 55D. 45
5.如图，在Rt△ABC中，∠ACB=90∘，BCAC=12，则下列结论中正确的是
( )
A. sinA=12B. sinB= 55C. csA= 55D. tanB=2
6.在正方形网格中，△ABC的位置如图所示，则sin∠BAC的值为( )
A. 35B. 34C. 45D. 43
7.如图，在4×4正方形网格中，点A，B，C为网格交点，AD⊥BC，垂足为D，则sin∠BAD的值为( )
A. 12B. 34C. 35D. 45
8.如果方程x2−8x+7=0的两个根分别是Rt△ABC的两条直角边的长，△ABC最小的角为∠A，那么tanA的值为( )
A. 4 37B. 312C. 17D. 17或 312
9.如图，在△ABC中，AB=AC=10，BC=12，点D为BC的中点，DE⊥AB于点E，则tan∠BDE的值等于( )
A. 65B. 56C. 34D. 43
10.如图，已知l1//l2//l3，相邻两条平行直线间的距离相等，若等腰直角三角形ABC的三个顶点分别在这三条平行直线上，则sin α的值是
( )
A. 13B. 617C. 55D. 1010
11.如图，直角三角形纸片的两直角边长分别为6，8，现将△ABC按如图所示的方式折叠，使点A与点B重合，折痕为DE，则sin∠CBE的值是( )
A. 45B. 623C. 725D. 724
12.如图，梯子跟地面的夹角为∠A，关于∠A的三角函数值与梯子的倾斜程度之间，叙述正确的是( )
A. sinA的值越小，梯子越陡B. csA的值越小，梯子越陡
C. tanA的值越小，梯子越陡D. 陡缓程度与∠A的函数值无关
第II卷（非选择题）
二、填空题（本大题共4小题，共12分）
13.如图，在Rt△ACB中，∠C=90°，AC=3，BC=4，则sinB的值是______．
14.等边△ABC中，点D在射线CA上，且AB=2AD，则tan∠DBC的值为______．
15.比较大小：sin81∘ tan47∘.(填“<”“=”或“>”)
16.如图，在△ABC中，点D在边BC上，AD⊥AC，∠BAD=∠C，BD=2，CD=6，那么tanC= ．
三、解答题（本大题共9小题，共72分。解答应写出文字说明，证明过程或演算步骤）
17.(本小题8分)
如图，在Rt△ABC中，∠C=90°，M是直角边AC上一点，MN⊥AB于点N，AN=3，AM=4，求cs B的值．
18.(本小题8分)
如图，点O是矩形ABCD的对角线AC的中点，过点O作AC的垂线交BC于点E，交AD于点F，连接FC，AE．
(1)点P在对角线AC上，且2AF2=AC·AP，求证：FP⊥AD．
(2)若AD=2AB，求tan∠CFD的值．
19.(本小题8分)
如图，射线OA放置在4×5的正方形虚线网格中，现请你在图中找出格点(即每个小正方形的顶点)B，并连接OB、AB使△AOB为直角三角形，并且
(1)使tan∠AOB的值为1；
(2)使tan∠AOB的值为12．
20.(本小题8分)
如图，在△ABC中，CD⊥AB，垂足为D.若AB=12，CD=6，tanA=32.求sinB+csB的值．
21.(本小题8分)
如图，在△ABC中，CD⊥AB，垂足为D.若AB=12，CD=6，tanA=32.求sinB+csB的值．
22.(本小题8分)
如图，在Rt△ABC中，∠C=90∘，D为AC上的一点，CD=3，AD=BD=5.求∠A的三个三角函数值．
23.(本小题8分)
如图，点P是∠α的边OA上的一点，已知点P的横坐标为6，若tanα=43，
(1)求点P的纵坐标;
(2)求∠α的其他三角函数值．
24.(本小题8分)
如图，在矩形ABCD中，E是BC边上的点，AE=BC，DF⊥AE，垂足为F，连接DE，
(1)求证：△ABE≌△DFA．
(2)如果AD=10，AB=6，求sin∠EDF的值．
25.(本小题8分)
如图，在Rt△ABC中，∠ABC=90∘，AB(1)求证：四边形AECF是菱形;
(2)若BEEC=14，则tan∠BCF的值为 ．
答案和解析
1.【答案】B
【解析】【分析】
本题主要考查了坡度的定义，比较容易.利用勾股定理求得水平距离，根据坡度定义求解．
【解答】
解：∵某人沿着有一定坡度的坡面前进了10米．此时他与水平地面的垂直距离为5米，
根据勾股定理可以求出他前进的水平距离为 102−52=5 3米．
所以这个坡面的坡度为55 3=1∶ 3．
故选B．
2.【答案】A
【解析】【分析】
本题考查了相似三角形的判定和性质，矩形的性质，三角函数的定义等知识；熟练掌握矩形的性质，证明三角形相似是解决问题的关键．
证明△BEF∽△DAF，得出EF=12AF，EF=13AE，由矩形的对称性得：AE=DE，得出EF=13DE，设EF=x，则DE=3x，由勾股定理求出DF= DE2−EF2=2 2x，再由三角函数定义即可得出答案．
【解答】
解：∵四边形ABCD是矩形，
∴AD=BC，AD//BC，
∵点E是边BC的中点，
∴BE=12BC=12AD，
∴△BEF∽△DAF，
∴EFAF=BEAD=12，
∴EF=12AF，
∴EF=13AE，
∵点E是边BC的中点，
∴由矩形的对称性得：AE=DE，
∴EF=13DE，设EF=x，则DE=3x，
∴DF= DE2−EF2=2 2x，
∴tan∠BDE=EFDF=x2 2x= 24；
故选A．
3.【答案】B
【解析】解：如图，取格点K，连接AK，BK．
观察图象可知AK⊥BK，BK=2AK，BK//CD，
∴∠AED=∠ABK，
∴tan∠AED=tan∠ABK=AKBK=12，
故选：B．
如图，取格点K，连接AK，BK.观察图象可知AK⊥BK，BK=2AK，BK//CD，推出∠AED=∠ABK，求出tan∠ABK即可．
本题考查解直角三角形，解题的关键是学会添加常用辅助线，学会用转化的思想思考问题，属于中考常考题型．
4.【答案】C
【解析】如图，延长AC到D，连接BD，
∵AD2=22+42=20，BD2=12+22=5，AB2=32+42=25，
∴AD2+BD2=AB2，
∴∠ADB=90∘，∴cs∠BAC=ADAB= 20 25=2 55.故选C．
5.【答案】D
【解析】∵在Rt△ABC中，∠ACB=90∘，BCAC=12，
∴设BC=x，AC=2x，则AB= 5x，
故sinA=BCAB=x 5x= 55，故A选项错误;
sinB=ACAB=2x 5x= 2 55，故B选项错误;
csA=ACAB=2x 5x=2 55，故C选项错误;
tanB=ACBC =2xx=2，故D选项正确．
故选D．
6.【答案】A
【解析】解：设小正方形的边长为1，作CD⊥AB的延长线于点D．
∵在Rt△ACD中，∠ADC=90°，CD=3，AC= 32+42=5，
∴sin∠BAC=CDAC=35，
故选A．
sin∠BAC的值可以转化为直角三角形的边的比的问题，因而过点C作CD垂直于AB的延长线于点D.在Rt△ADC中根据三角函数的定义求解．
本题考查了锐角三角函数的概念：在直角三角形中，正弦等于对边比斜边；余弦等于邻边比斜边；正切等于对边比邻边．也考查了勾股定理．
7.【答案】C
【解析】【分析】
本题考查了锐角三角函数的定义以及勾股定理，解题的关键熟记三角函数的定义并灵活运用．
先利用等面积法求出AD，在△ABD中，再利用勾股定理求出BD，利用正弦的定义求出sin∠BAD即可．
【解答】
解：如图，连接AC，
在Rt△BEC中，BC= BE2+CE2= 42+32=5，
∵AD⊥BC，
∵S△ABC=4×4−12×4×3−12×1×4=8，
∴12×BC×AD=8，
即12×5×AD=8，
解得AD=165，
在Rt△ADB中，BD= AB2−AD2=125，
∴sin∠BAD=BDAB=1254=35．
8.【答案】C
【解析】∵x2−8x+7=0，∴(x−7)(x−1)=0，
解得x1=1，x2=7．∴Rt△ABC的两条直角边的长为1，7．
∵∠A是最小的角，∴∠A所对的边长为1(小角对小边)，
∴tanA=17.故选C．
9.【答案】C
【解析】如图，连接AD，
在△ABC中，AB=AC=10，BC=12，D为BC的中点，
∴AD⊥BC，BD=12BC=6，∴AD= AB2−BD2=8，
∴tan∠BAD=BDAD=68=34．∵AD⊥BC，DE⊥AB，
∴∠BDE+∠ADE=90∘，∠BAD+∠ADE=90∘，∴∠BDE
=∠BAD，∴tan∠BDE=tan∠BAD=34.故选C．
10.【答案】D
【解析】【分析】
本题考查了全等三角形的判定与性质，等腰直角三角形的性质，锐角三角函数的定义，作辅助线构造出全等三角形是解题的关键．过点A作AD⊥l1于D，过点B作BE⊥l1于E，根据同角的余角相等求出∠CAD=∠BCE，然后利用“角角边”证明Rt△ACD和Rt△CBE全等，根据全等三角形对应边相等可得CD=BE，AD=CE，然后利用勾股定理列式求出AC，再根据勾股定理求出AB，然后利用锐角的正弦等于对边比斜边列式计算即可得解．
【解答】
解：如图，过点A作AD⊥l1于D，过点B作BE⊥l1于E，
设l1和l2之间的距离为h，则l2和l3之间的距离也为h．
∵∠CAD+∠ACD=90°，∠BCE+∠ACD=90°，
∴∠CAD=∠BCE，
在等腰直角三角形ABC中，AC=BC，
在Rt△ACD和Rt△CBE中，
{∠CAD=∠BCE∠ADC=∠BEC=90∘AC=CB,
∴Rt△ACD≌Rt△CBE(AAS)．
∴CD=BE=h，
∴AD=CE=2h，
在Rt△ACD中，
AC= AD2+CD2= 5h，
在等腰直角三角形ABC中，
AB= AC2+BC2= 10h．
∴sinα=sin∠ABF=AFAB=h 10h= 1010．
故选D．
11.【答案】C
【解析】由折叠的性质可知，EB=EA．
由题意得BC=6，AC=8，∠C=90∘，∴CE=8−BE，在Rt△BEC中，BE2=CE2+BC2，
∴BE2=(8−BE)2+62，解得BE=254，
则CE=8−BE=74.在Rt△BEC中，sin∠CBE=CEBE=725．
故选C．
12.【答案】B
【解析】解：tanA的值越大，梯子越陡；sinA的值越大，梯子越陡;csA的值越小，梯子越陡．
所以B正确．
故选：B．
根据锐角三角函数的增减性即可得到答案．
本题考查了锐角三角函数的增减性，熟记tanA的值越大，梯子越陡；sinA的值越大，梯子越陡;csA的值越小，梯子越陡．
13.【答案】35
【解析】【分析】
此题主要考查了勾股定理，以及锐角三角函数定义，关键是掌握正弦：锐角A的对边a与斜边c的比叫做∠A的正弦．
首先利用勾股定理计算出AB，再根据正弦定义进行计算．
【解答】
解：∵∠C=90°，AC=3，BC=4，
∴AB= 32+42=5，
∴sinB=ACAB=35．
14.【答案】 33或3 3
【解析】解：如图①，当D在AC之间
∵在等边△ABC中，
AB=AC=BC，∠C=60°，
∵AB=2AD，
∴AD=CD，
∴BD⊥AC，
∴∠BDC=90°，
∴∠DBC=30°，
∴tam∠DBC= 33；
如图②，当D在CA延长线上时，过点D作DE⊥BC于E，
∵在等边△ABC中，
AB=AC=BC，∠C=60°，
∵AB=2AD，
∴设AD=x，则AB=AC=BC=2x，
∵DE⊥BC，
∴∠DEC=90°，
∴∠CDE=30°，
∴EC=12DC=1.5x，ED=3 32x，BE=0.5x，
∴tan∠DBC=DEBE=3 3，
故答案为：3 3或 33．
分两种情况讨论，并画出图形，①当D在AC之间，根据等边三角形的性质，求出AB=AC=BC，∠C=60°，
再根据AB=2AD，得出∠BDC=90°，从而求出tam∠DBC的值；②当D在CA延长线上时，过点D作DE⊥BC于E，设AD=x，则AB=AC=BC=2x，在Rt△DEC中用三角函数表示两条直角边，从而求出tan∠DBC的值．
本题主要考查了锐角三角函数，等边三角形的性质，掌握等边三角形的性质的应用，分情况讨论，作出相应的图形是解题关键．
15.【答案】<
【解析】略
16.【答案】12
【解析】∵BD=2，CD=6，∴BC=BD+CD=8．
∵∠B=∠B，∠BAD=∠C，
∴△ABD∽△CBA，∴ADAC=ABBC=BDAB，
∴AB2=BD⋅BC=2×8=16，∴AB=4．
∵AD⊥AC，∴tanC=ADAC=ABBC=48=12．
17.【答案】解：∵∠C=90°，MN⊥AB，
∴∠C=∠ANM=90°，
又∵∠A=∠A，
∴△AMN∽△ABC，
∴ANAM=ACAB=34，
设AC=3x，AB=4x，
由勾股定理得BC= AB2−AC2= 7x，
∴在Rt△ABC中，csB=BCAB= 7x4x= 74．
【解析】本题考查了相似三角形的判定与性质，勾股定理，锐角三角函数的定义.易证△AMN∽△ABC，根据相似三角形的对应边成比例可得ANAM=ACAB=34，设AC=3x，AB=4x，利用勾股定理得到BC= AB2−AC2= 7x，即可根据余弦的定义得到答案．
18.【答案】(1)证明：∵EF⊥AC，∴∠AOF=90°.∵点O是AC的中点，∴AC=2OA.∵2AF2=AC·AP，∴2AF2=2AO·AP.∴AF2=AO·AP.∴ AFAO=APAF . 又∵∠DAC=∠DAC，∴△AFP∽△AOF.∴∠AFP=∠AOF=90°，∴FP⊥AD．
(2)解：设AB=a，AD=2a.∵四边形ABCD是矩形，∴AB=CD=a，∠D=90°.∵OA=OC，EF⊥AC，∴AF=FC. 设DF=x，则AF=FC=2a−x. 在Rt△CDF中，∠CDF=90°，∴由勾股定理，得CD2+DF2=CF2，∴a2+x2=(2a−x)2，∴ x=34a .∴ DF=34CD .∴ tan∠CFD=CDDF=43 . 答：tan∠CFD的值为 43 ．
【解析】略
19.【答案】解：(1)如图1所示：
∵OA= 10，且tan∠AOB=1，∴AB=OB= 5，∴可找到格点B．
(2)如图2所示；
同上一问的解法，可以求得AB= 2，OB=2 2.即可找到点B．
【解析】此题主要考查了应用设计与作图，利用锐角三角函数关系得出是解题关键．
根据tan∠AOB的值分别为1、12，构造直角三角形进而得出答案．
20.【答案】在Rt△ACD中，CD=6，tanA=CDAD=6AD=32，所以AD=4，所以BD=AB−AD=8.在Rt△BCD中，BC= BD2+CD2= 82+62=10，所以sinB=CDBC=610=35，csB=BDBC=810=45，所以sinB+csB=35+45=75．
【解析】见答案
21.【答案】解：在Rt△ACD中，∵∠ADC=90°，
∴tanA=CDAD=32，CD=6，
∴AD=4，
∴BD=AB−AD=12−4=8．
在Rt△BCD中，
∵∠BDC=90°，BD=8，CD=6，
∴BC=10，
∴sinB=CDBC=35，csB=BDBC=45，
∴sinB+csB=75．
【解析】本题考查了锐角三角函数的定义，勾股定理有关知识，先在Rt△ACD中，由正切函数的定义得tanA=CDAD=32，求出AD=4，则BD=AB−AD=8，再在Rt△BCD中，由勾股定理得BC=10，sinB=CDBC=35，csB=BDBC=45，由此求出sinB+csB的值．
22.【答案】在Rt△BCD中，∵CD=3，BD=5，
∴BC= BD2−CD2= 52−32=4．
又AC=AD+CD=8，
∴AB= AC2+BC2= 82+42=4 5．
∴sinA=BCAB=44 5= 55，csA=ACAB=84 5=2 55，
tanA=BCAC=48=12．

【解析】见答案
23.【答案】【小题1】
如图，过P作PM⊥x轴于M，则∠PMO=90∘，
∵点P的横坐标为6，∴OM=6．
∵tanα=PMOM=PM6=43，
∴PM=8，∴点P的纵坐标是8．
【小题2】
在Rt△OMP中，
∵∠PMO=90∘，PM=8，OM=6，
∴OP= PM2+OM2= 82+62=10，
∴sinα=PMOP=810=45，csα=OMOP=610=35．

【解析】1. 见答案
2. 见答案
24.【答案】(1)证明：∵在矩形ABCD中，BC=AD=AE，AD/​/BC，∠B=90∘，
∴∠DAF=∠AEB，
∵DF⊥AE，
∴∠AFD=90∘=∠B，
又∵AE=BC=AD．
∴△ABE≌△DFA．
(2)解：由(1)知△ABE≌△DFA．
∴AB=DF=6．
在Rt△ADF中，AF= AD2−DF2= 102−62=8，
∴EF=AE−AF=AD−AF=2，
在Rt△DFE中，DE= DF2+EF2= 62+22=2 10，
∴sin∠EDF=EFDE=22 10= 1010．
【解析】本题主要考查矩形的性质，全等三角形的判定与性质以及锐角三角函数的定义，熟练运用矩形的性质和判定，能够找到证明全等三角形的有关条件；运用全等三角形的性质和勾股定理求得三角形中的边，再根据锐角三角函数的概念求解．
(1)根据矩形的对边平行且相等得到AD=BC=AE，∠DAF=∠AEB.再结合一对直角相等即可证明三角形全等；
(2)根据全等三角形的对应边相等以及勾股定理，可以求得AF，EF的长；再根据勾股定理求得DE的长，运用三角函数定义求解．
25.【答案】【小题1】
证明：∵点D是AC的中点，
∴AD=CD．∵DF=DE，
∴四边形AECF是平行四边形．
又∵DE⊥AC，∴平行四边形AECF是菱形．
【小题2】
15

【解析】1. 见答案
2.
设BE=a，则CE=4a.由菱形的性质得AE=CE=4a，AE/​/CF，则∠BEA=∠BCF.再由勾股定理得AB= 15a，然后由锐角三角函数的定义即可得出结论．