初中数学北师大版九年级下册1 圆精品当堂达标检测题

这是一份初中数学北师大版九年级下册1 圆精品当堂达标检测题，共19页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共12小题，共36分。在每小题列出的选项中，选出符合题目的一项）
1.下列各图形中，各个顶点一定在同一个圆上的是
．( )
A. 正方形B. 菱形C. 平行四边形D. 梯形
2.有一架竖直靠在直角墙面的梯子正在下滑，一只猫紧紧盯住位于梯子正中间的老鼠，等待与老鼠距离最小时扑捉．把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图，∠ABC=90°，点M、N分别在射线BA、BC上，MN长度始终保持不变，MN=4，E为MN的中点，点D到BA、BC的距离分别为3和2，在此滑动过程中，猫与老鼠的距离DE的最小值为．( )
A. 2 5−2B. 13−1C. 13−2D. 13−3
3.在平面内与点A的距离为2 cm的点的个数为
( )
A. 无数个B. 2个C. 1个D. 0个
4.下列圆中既有圆心角又有圆周角的是
A. B. C. D.
5.如图，点P(x,y)在以坐标原点O为圆心，5为半径的圆上．若x，y都是整数，则这样的点P一共有( )
A. 4个B. 8个C. 12个D. 以上都不对
6.如图，△ABC中，AB=5，AC=4，BC=2，以A为圆心AB为半径作圆A，延长BC交圆A于点D，则CD长为( )
A. 5B. 4C. 92D. 2 5
7.在等腰△ABC中，AB=AC，∠BAC=30°，点P在以A为圆心，BC长为半径的圆上，且BP=BA，则∠PBC的度数为( )
A. 105°B. 150°C. 45°或105°D. 90°或150°
8.如图，△ABC中，∠A=48°，O是BC的中点，以O为圆心，OB长为半径画弧，分别交AB，AC于点D，E，连接OD，OE，则∠DOE的度数是( )
A. 54°B. 64°C. 74°D. 84°
9.如图，已知AB，AD是⊙O的弦，∠B=30°，点C在弦AB上，连接CO并延长CO交⊙O于点D，∠D=20°，则∠BAD的度数是( )
A. 30°B. 40°C. 50°D. 60°
10.圆O的直径AB=26cm，点C是圆O上一点(不与点A、B重合)，作CD⊥AB于点D，若CD =12cm，则AD的长是
( )
A. 8cmB. 18cmC. 8cm或18cmD. 16cm
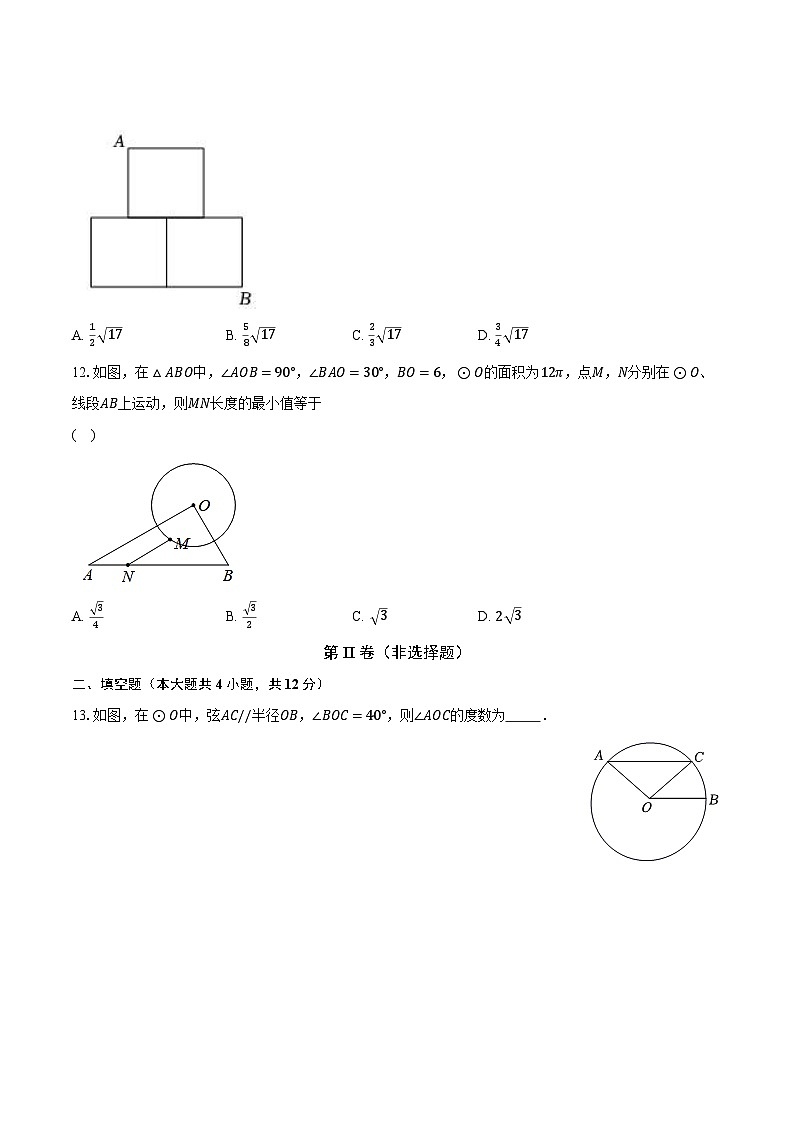
11.如图是由三个大小相同的正方形组成的“品”字型轴对称图案，测得顶点A，B之间的距离为5.现用一个半径为r的圆形纸片将其完全覆盖，则r的最小值是( )
A. 12 17B. 58 17C. 23 17D. 34 17
12.如图，在△ABO中，∠AOB=90°，∠BAO=30°，BO=6，⊙O的面积为12π，点M，N分别在⊙O、线段AB上运动，则MN长度的最小值等于
( )
A. 34B. 32C. 3D. 2 3
第II卷（非选择题）
二、填空题（本大题共4小题，共12分）
13.如图，在⊙O中，弦AC/​/半径OB，∠BOC=40°，则∠AOC的度数为 ．
14.如图，在Rt△ABC中，∠C=90°，AB=12.若以点C为圆心，CB长为半径的圆恰好经过AB的中点D，则AC的长为 ．
15.著名画家达·芬奇不仅画艺超群，同时还是一位数学家、发明家．他曾经设计过一种如图所示的圆规，有两个互相垂直的滑槽(滑槽的宽度忽略不计)，一根没有弹性的木棒两端A、B能在滑槽内自由滑动，将笔插入位于木棒中点P处的小孔中，随着木棒的滑动就可以画出一个圆．若AB=20 cm，则画出的圆的半径为 cm．
16.如图所示的正方形网格中，O，A，B，C，D是网格线交点，若CD与AB所在圆的圆心都为点O，则CD与AB的长度之比为 ．
三、解答题（本大题共9小题，共72分。解答应写出文字说明，证明过程或演算步骤）
17.(本小题8分)
如图，AB、CD是⊙O的两条弦．若∠AOB+∠C=180°，∠COD=∠A，求∠AOB的度数．
18.(本小题8分)
已知△ABC，AB=AC．
(1)求作：△ABC的外接圆;(要求：尺规作图，保留作图痕迹，不写作法)
(2)若△ABC的外接圆的圆心O到BC边的距离为4，BC=12，求⊙O的面积．
19.(本小题8分)
由于过度采伐森林和破坏植被，使我国某些地区多次受到沙尘暴的侵袭．近日，A市气象局测得沙尘暴中心在A市正东方向400 km的B处，正向西北方向转移，如图所示，距沙尘暴中心300 km的范围内将受到影响，则A市是否会受到这次沙尘暴的影响？
20.(本小题8分)
已知：如图，AB是⊙O的直径，CD是⊙O的弦，AB，CD的延长线交于E，若AB=2DE，∠E=18°，求∠C及∠AOC的度数．
21.(本小题8分)
如图，△ABC中，AB=AC，⊙O是△ABC的外接圆，BO的延长线交边AC于点D．
(1)求证：∠BAC=2∠ABD;
(2)当△BCD是等腰三角形时，求∠BCD的大小．
22.(本小题8分)
如图，半圆O的直径AB=8，半径OC⊥AB，D为AC上一点，DE⊥OC，DF⊥OA，垂足分别为E，F，求EF的长．
23.(本小题8分)
如图，AB是⊙O的直径，点C在⊙O上，CD⊥AB，垂足为D，已知CD=4，OD=3，求AB和CB的长．
24.(本小题8分)
如图，已知在△ABC中，∠A=90∘．
(1)请用圆规和直尺作出⊙P，使圆心P在AC边上，且与AB，BC两边都相切(保留作图痕迹，不写作法和证明);
(2)若∠ABC=60∘，AB=3，求⊙P的面积．
25.(本小题8分)
如图，AC是⊙O的直径，点B在圆周上(不与点A、C重合)，点D在AC的延长线上，连接BD交⊙O于点E，∠AOB=3∠D.求证：DE=OB．
答案和解析
1.【答案】A
【解析】解：∵正方形对角线相等且互相平分，
∴四个顶点到对角线交点距离相等，
∴正方形四个顶点定可在同一个圆上．
故选：A．
四个顶点可在同一个圆上的四边形，一定有一点到它的四个顶点的距离都相等，因而B、C、D都是错误的；正方形的四个顶点到对角线的交点的距离都相同，因而正方形的四个顶点一定可以在同一个圆上．
此题主要考查了圆的认识，能够理解四个顶点在同一个圆上的条件是解决本题的关键．
2.【答案】C
【解析】连接BE、BD，
由勾股定理，得BD= 32+22= 13，
∵在Rt△MBN中，点E是MN的中点，MN=4，
∴BE=12MN=2，
∴点E的运动轨迹是以B为圆心，2为半径的弧，
∴当点E落在线段BD上时，DE的值最小，
∴DE的最小值为 13−2.故选C．
3.【答案】A
【解析】解：所有到定点A的距离等于2cm的点在以点A为圆心，2cm为半径的圆上．
故选：A．
在平面内与点A的距离为2cm的点在“以点A为圆心，2cm为半径为的圆”上．
本题主要考查了圆的相关概念．
4.【答案】B
【解析】【分析】
本题考查了圆周角与圆心角的识别，熟记圆周角与圆心角的定义与图形特征是解题的关键．根据圆周角的定义：顶点在圆周上，角的两边与圆相交的角是圆周角；圆心角的定义：顶点在圆心，两条边都与圆周相交的角是圆心角．进行判断便可．
【解答】
解：A.图中只有圆周角，没有圆心角，选项不符合题意；
B.图中既有圆心角，也有圆周角，选项符合题意；
C.图中只有圆心角，没有圆周角，选项不符合题意；
D.图中只有圆心角，没有圆周角，选项不符合题意；
故选：B．
5.【答案】C
【解析】根据题意，得x2+y2=25.其整数解为x=0,y=±5;x=±3,y=±4;x=±4,y=±3;x=±5,y=0.所以这样的点P一共有12个．
6.【答案】C
【解析】【分析】本题主要考查勾股定理的应用及圆的有关性质。连接AD，并作BD边上的垂线，由于AB与AD均为圆的半径，则△ADB为等腰三角形，由三线合一的性质可知DE=BE，在Rt△AEB和Rt△AEC中，利用勾股定理即可求得EC的长度，从而可求CD的长度。
【解答】
连接AD，过点A作BD边上的垂线，垂足为E，如图所示：
因为AE⊥BD，则△AEC与△AEB均为直角三角形；
设AE=x，EC=y，由勾股定理得：
x2+y2=42①，
x2+(y+2)2=52②，
联立①②可得：y=54，
则EC=54，
因为AB、AD均为圆A的半径，所以△ADB为等腰三角形，利用三线合一的性质可知：ED=EB，
则CD=54+54+2=92。
故答案为：C．
7.【答案】C
【解析】解：如图，当点P在直线AB的右侧时，连接AP，
∵AB=AC，∠BAC=30°，
∴∠ABC=∠C=75°，
∵AB=AB，AC=PB，BC=PA，
∴△ABC≌△BAP(SSS)，
∴∠ABP=∠BAC=30°，
∴∠PBC=∠ABC−∠ABP=45°，
当点P′在AB的左侧时，同法可得∠ABP′=30°，
∴∠P′BC=30°+75°=105°，
故选：C．
分两种情形，利用全等三角形的性质即可解决问题．
本题考查圆的相关概念，全等三角形的判定和性质、等腰三角形的性质等知识，解题的关键是学会用分类讨论的思想思考问题．
8.【答案】D
【解析】解：如图，由题意得：OC=OB=OD=OE．
∴∠BDO=∠B，∠CEO=∠C，
∵∠A=48°，
∴∠B+∠C=180°−∠A=132°，
∴∠CEO+∠BDO=132°，
∴∠AEO+∠ADO=360°−132°=228°，
∴∠DOE=360°−∠A−∠AEO−∠ADO=360°−48°−228°=84°．
故选：D．
根据圆中半径相等，得到∠BDO=∠B，∠CEO=∠C，利用三角形内角和定理，平角的定义，以及四边形的内角和为360°，进行计算即可．
本题考查圆的基本概念，三角形的内角和定理．熟练掌握圆中半径都相等，利用等边对等角，进行求解，是解题的关键．
9.【答案】C
【解析】【分析】
本题考查的是圆的性质和等腰三角形的性质及角的计算，掌握圆的半径相等和等边对等角是解题的关键．连接OA，根据圆的半径相等证明∠OAB=∠B和∠OAD=∠D，得到答案．
【解答】
解：连接OA，
∵OA=OB，
∴∠OAB=∠B=30°，
∵OA=OD，
∴∠OAD=∠D=20°，
∴∠BAD=∠OAB+∠OAD=50°，
故选：C．
10.【答案】C
【解析】【分析】
本题考查了勾股定理，圆的性质，熟练掌握勾股定理是解题的关键．
分两种情况画出图形，由勾股定理求出OD=5cm，则可得出答案．
【解答】
解：当点D在OB上，如图，连接OC，
∵圆O的直径AB=26cm，
∴OA=OC=13cm，
∵CD⊥AB，
∴∠ODC=90°，
∴DO= OC2−CD2= 132−122=5(cm)，
∴AD=OA+OD=13+5=18(cm);
当点D在线段OA上时，如图，
同理可得出AD=AO−OD=13−5=8(cm)．
故选：C．
11.【答案】B
【解析】【分析】
此题考查圆的有关概念，掌握圆的有关概念和勾股定理是解题关键．
根据AB=5，求出每个小正方形的边长，再由勾股定理和半径相等列方程组求解．
【解答】
解：如图，设BE=x．
在Rt△ACB中，AC=2x，BC=32x，
(2x)2+(32x)2=52，
解得x=2(负值舍去)，
∴EH=4，DH=1，
圆心O在图形的对称轴上，设OE=a，OD=OB=r，
a2+22=r2(4−a)2+12=r2
解得：r=58 17(负值舍去)，
∴r的最小值是58 17．
故选B．
12.【答案】C
【解析】【分析】
本题考查圆的相关概念，三角形三边之间的关系，垂线段最短，直角三角形的性质等知识．
作OC⊥AB，交AB于C，交⊙O于D，则CD=OC−OD，即CD是MN的最小值，根据含30°角的直角三角形的性质得出OA、OC，求出半径，即可解答．
【解答】
解：作OC⊥AB，交AB于C，交⊙O于D，则CD=OC−OD，即CD是MN的最小值，
∵∠AOB=90°，∠BAO=30°，BO=6，
∴AB=12，
∴AO=6 3
∵OC⊥AB，
∴OC=12OA=3 3，
∵⊙O的面积为12π，
∴OD= 12=2 3，
∴CD=OC−OD= 3，
∴MN长度的最小值等于 3．
13.【答案】100°
【解析】【分析】
本题考查了三角形内角和：三角形内角和是180°.也考查了等腰三角形的性质和圆的认识．先根据平行线的性质得到∠OCA=∠BOC=40°，然后根据圆半径都相等，结合等腰三角形的性质和三角形内角和定理计算∠AOC的度数．
【解答】
解：∵AC/​/OB，
∴∠OCA=∠BOC=40°，
∵OA=OC，
∴∠OAC=∠OCA=40°，
∴∠AOC=180°−∠OAC−∠OCA
=180°−40°−40°
=100°．
故答案为100°．
14.【答案】6 3
【解析】略
15.【答案】10
【解析】略
16.【答案】 2：1
【解析】解：由勾股定理得，OC=OD= 22+22=2 2，
则OC2+OD2=CD2，
∴∠COD=90°，
∴CD与AB的长度之比=90π×2 2180：90π×2180= 2：1，
故答案为： 2：1．
根据勾股定理分别求出OC、OD，根据勾股定理的逆定理得到∠COD=90°，根据弧长公式计算，得到答案．
本题考查的是弧长的计算，掌握弧长公式l=nπr180是解题的关键．
17.【答案】设∠COD=∠A=x.∵OA=OB，∴∠A=∠B=x.∴在△OAB中，∠AOB=180°−2x.又∵OC=OD，∴∠C=∠D.∴在△COD中，∠C=12180∘−x.∵∠AOB+∠C=180°，∴180∘−2x+12180∘−x=180∘，解得x=36°.∴∠AOB=180°−2x=180°−2×36°=108°
【解析】见答案
18.【答案】略
【解析】略
19.【答案】如图，过点A作AC⊥BD于点C，由题意，得AB=400 km，∠DBA=45°，所以AC=BC．
在Rt△ABC中，设AC=BC=x．
由勾股定理，得AC2+BC2=AB2，
所以x2+x2=4002，所以AC=x=200 2≈282.8(km)
因为282.8 km<300 km，
所以A市将受到这次沙尘暴的影响．

【解析】见答案
20.【答案】解：连接OD，

∵AB=2DE=2OD，
∴OD=DE，又∠E=18°，
∴∠DOE=∠E=18°，
∴∠ODC=36°，
同理∠C=∠ODC=36°
∴∠AOC=∠E+∠OCE=54°.

【解析】本题考查了圆的认识，等腰三角形的性质等有关知识，要求∠ AOC的度数，由AB=2DE知DE与半径相等，连接OD构造等腰△ODE和等腰△OCD，得到∠C=∠ODC=36°，由图知∠ AOC=∠ C+∠ E，进行求解即可．
21.【答案】【小题1】
【证明】连接AO并延长，交BC于E，如图．∵AB=AC，∴弧AB=弧AC．∵AE过圆心O，∴AE垂直平分弦BC，∴AE平分∠BAC，∴∠BAC=2∠BAE．∵OA=OB，∴∠ABD=∠BAE，∴∠BAC=2∠ABD．
【小题2】
设∠ABD=x.由(1)知∠BAC=2∠ABD=2x，∴∠BDC=3x．∵△BCD是等腰三角形，则分两种情况进行讨论：
①若BD=BC，则∠C=∠BDC=3x．∵AB=AC，∴∠ABC=∠C=3x.在△ABC中，∵∠ABC+∠C+∠BAC=180°，∴3x+3x+2x=180°，解得x=22.5°，∴∠BCD=3x=67.5°．
②若BC=CD，则∠BDC=∠CBD=3x，∴∠ABC=∠ACB=4x.在△ABC中，∵∠ABC+∠C+∠BAC=180∘，∴4x+4x+2x=180∘，∴x=18°，∴∠BCD=4x=72°．
综上所述，当△BCD是等腰三角形时，∠BCD的大小为67.5°或72°．

【解析】1. 见答案
2. 见答案
22.【答案】解：如图，连接OD．
∵OC⊥AB，DE⊥OC，DF⊥OA，
∴∠AOC=∠DEO=∠DFO=90∘，
∴四边形DEOF是矩形，∴EF=OD．
∵OD=OA=12AB=4，∴EF=4．

【解析】本题考查了圆的认识及矩形的判定与性质，解题的关键是利用矩形的判定方法判定四边形DFOE为矩形．连接OD，利用三个角是直角的四边形是矩形判定四边形DEOF是矩形，利用矩形的对角线相等即可得到所求结论．
23.【答案】解：连接OC，BC，
∵CD⊥AB，垂足为D，CD=4，OD=3，
∴OB=OC= OD2+CD2= 32+42=5，
∴AB=2OC=10；
∴BD=OB−OD=2，
∴BC= BD2+CD2= 42+22=2 5．
【解析】本题考查的是圆的相关概念，勾股定理的知识，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
连接OC、BC，根据勾股定理求出OC的长，进而可得出AB的长，进一步求出BD，再利用勾股定理求出BC的长，即可得到结论．
24.【答案】解：(1)如图所示，则⊙P为所求作的圆．
(2)∵∠B=60°，BP平分∠ABC，
∴∠ABP=30°，
∵∠BAC=90°，
∴BP=2AP，
在Rt△ABP中，
AB2+AP2=BP2，
∴32+AP2=4AP2，
∴AP= 3，
∴⊙P的面积为 32π=3π．
【解析】本题考查的是基本作图，角平分线，勾股定理，含30°直角三角形有关知识．
(1)作∠ABC的平分线交AC于P，再以P为圆心，PA为半径即可作出⊙P；
(2)根据角平分线的定义得到∠ABP=30°，得出BP=2AP，然后再利用勾股定理求出AP，最后求出⊙P的面积即可．
25.【答案】解：如图，连接EO．
设∠D=x．
∵OB=OE，
∴∠B=∠OEB．
∵∠OEB是△DEO的外角，
∴∠OEB=∠D+∠DOE=x+∠DOE．
∵∠AOB是△BOD的外角，
∴∠AOB=∠B+∠D=∠OEB+∠D=x+∠DOE+x=∠DOE+2x．
∵∠AOB=3∠D=3x，
∴∠DOE+2x=3x，即∠DOE=x=∠D.
∴DE=OE．
∴DE=OB．
【解析】见答案．