初中数学北师大版九年级下册2 圆的对称性精品同步测试题

这是一份初中数学北师大版九年级下册2 圆的对称性精品同步测试题，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共12小题，共36分。在每小题列出的选项中，选出符合题目的一项）
1.如图，C，D为半圆的三等分点，则下列结论： ①AD=CD=BC; ②∠AOD=∠DOC=∠COB; ③AD=CD=OC; ④△ADO绕点D逆时针旋转60∘与△ODC重合.其中正确的共有( )
A. 1个B. 2个C. 3个D. 4个
2.如图，在⊙O中，∠AOB=2∠COD，则AB与2CD的大小关系是
( )
A. AB>2CDB. AB<2CDC. AB=2CDD. 不能确定
3.如图，AB、AC是⊙O的两条弦，OE⊥AC，OF⊥AB，垂足分别E、F，若∠EOF=55°，则∠BOC的度数等于( )
A. 125°
B. 120°
C. 115°
D. 110°
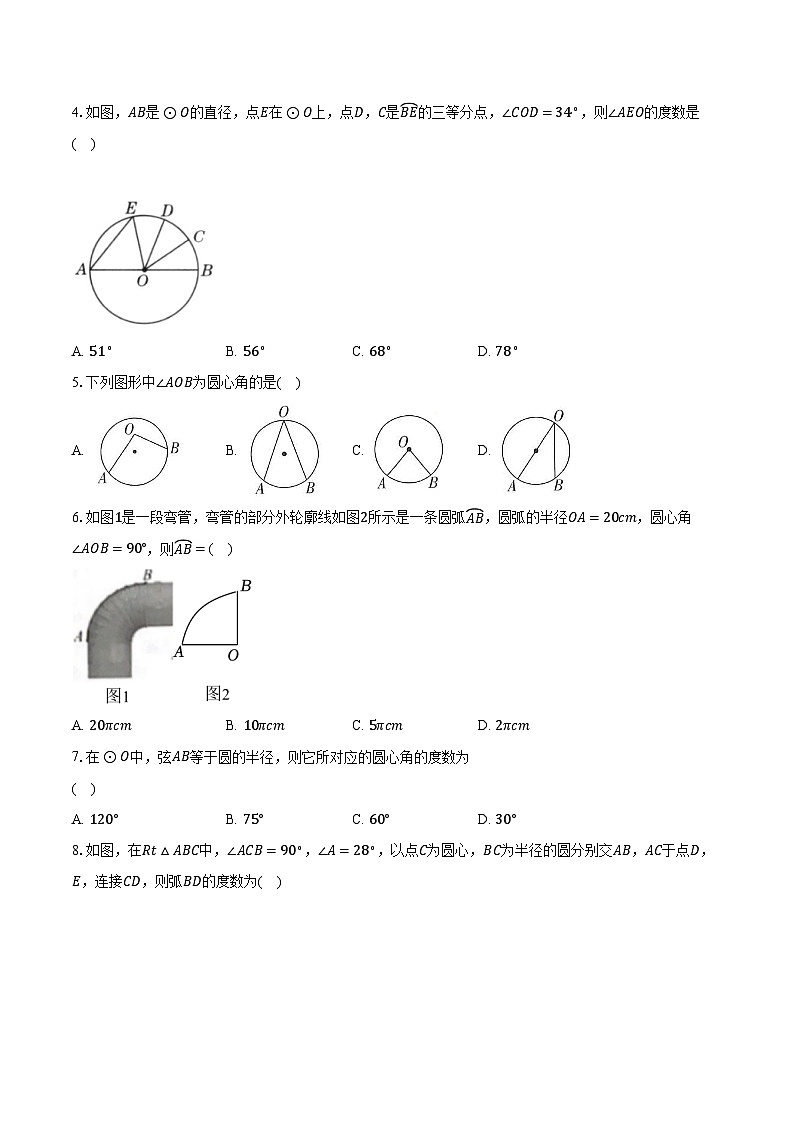
4.如图，AB是⊙O的直径，点E在⊙O上，点D，C是BE的三等分点，∠COD=34∘，则∠AEO的度数是
( )
A. 51∘B. 56∘C. 68∘D. 78∘
5.下列图形中∠AOB为圆心角的是( )
A. B. C. D.
6.如图1是一段弯管，弯管的部分外轮廓线如图2所示是一条圆弧AB，圆弧的半径OA=20cm，圆心角∠AOB=90°，则AB=( )
A. 20πcmB. 10πcmC. 5πcmD. 2πcm
7.在⊙O中，弦AB等于圆的半径，则它所对应的圆心角的度数为
( )
A. 120°B. 75°C. 60°D. 30°
8.如图，在Rt△ABC中，∠ACB=90∘，∠A=28∘，以点C为圆心，BC为半径的圆分别交AB，AC于点D，E，连接CD，则弧BD的度数为( )
A. 28∘B. 64∘C. 56∘D. 124∘
9.在⊙O中，若圆心角∠AOB=2∠COD，则AB与2CD的大小关系是( )
A. AB=2CDB. AB>2CDC. AB<2CDD. 不能确定
10.如图，AB是⊙O的直径，EF，EB是⊙O的弦，且EF=EB，EF与AB交于点C，连接OF，若∠AOF=40°，则∠OFE的度数是( )
A. 30°B. 20°C. 40°D. 35°
11.如图，△ABC的外接圆上，AB，BC，CA三弧的度数比为12:13:11.自劣弧BC上取一点D，过D分别作直线AC，直线AB的平行线，且交BC于E，F两点，则∠EDF的度数为．( )
A. 55°B. 60°C. 65°D. 70°
12.已知在扇形OAB中，∠AOB=90°，OB=4，C为弧AB的中点，D为半径OB上一动点，点B关于直线CD的对称点为M，若点M落在扇形OAB内(不含边界)，则OD长的取值范围是( )
A. 4 2−4B. 2 2C. 0D. 4−2 2第II卷（非选择题）
二、填空题（本大题共4小题，共12分）
13.如图，AB是⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于E点，若AB=2DE，∠E=14∘，则弧AC的度数为 ∘.
14.如图，点A在半圆O上，BC是直径，AB⌢=AC⌢.若AB=2，则BC的长为 ．
15.如图，AB和DE是⊙O的直径，弦AC // DE.若弦BE=3，则弦CE的长为 ．
16.如图，半径为4的扇形OAB中，∠O=60°，C为半径OA上一点，过C作CD⊥OB于点D，以CD为边向右作等边△CDE，当点E落在AB⌒上时，CD=______．
三、解答题（本大题共9小题，共72分。解答应写出文字说明，证明过程或演算步骤）
17.(本小题8分)
如图，AD=CB，求证：AB=CD．
18.(本小题8分)
如图，⊙O的弦AB、CD的延长线相交于点P，且PA=PC.求证：AB=CD．
19.(本小题8分)
如图，⊙O中，弦AB与CD相交于点E，AB=CD，连接AD、BC．
求证：(1)AD=BC；
(2)AE=CE．
20.(本小题8分)
如图，AB，DE是⊙O的直径，C是⊙O上的一点，且AD=CE.
(1)求证：BE=CE；
(2)若∠B=50°，求∠AOC的度数．
21.(本小题8分)
如图，A、B、C、D是⊙O上四点，且AD=CB，求证：AB=CD．
22.(本小题8分)
如图，在边长为1的正方形网格纸中，以O为圆心，OA为半径作圆，点O、A、B均在格点上.仅用无刻度直尺，完成下列作图(不写作法，保留作图痕迹)：
(1)在图①中，作AB的中点M；
(2)在图②中，作BN，使得BN=AB．
23.(本小题8分)
如图：AC=BC，CD⊥OA于D，CE⊥OB于E，求证：CD=CE．
24.(本小题8分)
在扇形AOC中，∠AOC=60∘，点B在AC上，且AB=2BC，点E在半径OB上，以OE，OA为邻边作平行四边形OAFE，当点C，B，F共线时，
(1)求∠CFA的度数;
(2)求证：CF=OC．
25.(本小题8分)
如图所示，⊙O的弦BD，CE所在直线相交于点A，若AB=AC，求证：BD=CE．
答案和解析
1.【答案】D
【解析】【分析】
此题考查了圆心角，弧，弦之间的关系，关键是熟练掌握它们之间的关系.根据等分，可得圆心角相等，弧相等，弦相等，从而判断①②③的正误；根据等分可得圆心角的度数，从而可得两三角形的关系，即可判断④的正误．
【解答】
解：因为C，D为半圆的三等分点，所以AD=CD=BC，故 ①正确;
在同圆或等圆中，等弧所对的圆心角相等，所对的弦相等，
所以∠AOD=∠DOC=∠COB，AD=CD=BC．
又因为∠AOD+∠DOC+∠COB=180∘，
所以∠AOD=∠DOC=∠COB=60∘．
易知△AOD，△DOC和△COB为全等的等边三角形，故 ② ③ ④正确．
故选D．
2.【答案】C
【解析】【分析】
本题考查了圆心角，弧，弦的关系，根据圆心角，弧，弦的关系直接进行求解即可．
【解答】
解：∵在⊙O中，∠AOB=2∠COD，
∴AB=2CD，
故选C．
3.【答案】D
【解析】解：如图，设OF交AC于点J．
∵OE⊥AC，OF⊥AB，
∴∠OEJ=∠AFJ=90°，
∵∠OJE=∠AJF，
∴∠EOF=∠FAJ=55°，
∴∠BOC=2∠CAB=110°，
故选：D．
如图设OF交AC于点J.证明∠CAB=∠EOF=55°，可得结论．
本题考查圆周角定理，三角形内角和定理等知识，解题关键是灵活运用所学知识解决问题．
4.【答案】A
【解析】【分析】
此题考查的是圆心角，弧，弦的关系.在同圆中，由弧等可得到所对的圆心角相等，由此可求出∠BOE的度数，再根据互补关系可求出∠AEO的度数．
【解答】
解：∵C、D是BE上的三等分点，
∴DE=CD=BC，
∴∠DOE=∠COD=∠BOC=34°，
∴∠BOE=3∠COD=102°，
∵AB是⊙O的直径，
∴∠AOE=180°−∠BOE=180°−102°=78°．
∵OA=OE，
∴∠AEO=∠A，
∴∠AEO=12(180°−∠AOE)=12×(180°−78°)=51°．
故选A．
5.【答案】C
【解析】圆心角的特征： ①角的顶点是圆心; ②角的两边与圆相交，只有C选项符合.故选C．
6.【答案】B
【解析】【分析】
本题考查弧长的计算，关键是掌握弧长公式．
由弧长公式：l=nπr180(n是弧的圆心角的度数，r是弧的半径长)，即可计算．
【解答】
解：∵圆弧的半径OA=20cm，圆心角∠AOB=90°，
∴AB的长=90π×20180=10π(cm)．
故选：B．
7.【答案】C
【解析】本题考查的是圆心，弦，弧有关知识．
根据题意画出图形，判断出△OAB是等边三角形，再求出弦所对的圆心角的度数．
【解答】
解：如图，AB是⊙O的一条弦，OA=OB是⊙O的半径，
∵AB=OA=OB，
∴△OAB是等边三角形，
∴∠AOB=60°，
故选C．
8.【答案】C
【解析】∵∠ACB=90∘，∠A=28∘，∴∠B=62∘∵CB=CD，∴∠CDB=∠B=62∘，∴∠BCD=180∘−62∘−62∘=56∘，∴BD的度数为56∘.故选C．
9.【答案】C
【解析】如图，作∠AOB的平分线OE，交⊙O于E，∵OE平分∠AOB，∴∠AOE=∠EOB．∵∠AOB=2∠COD，∴∠AOE=∠EOB=∠COD，∴AE=BE=CD，∴AE=BE=CD，∵AE+BE>AB，∴AB<2CD.故选C．
10.【答案】D
【解析】【分析】
本题考查圆心角，弧，弦之间的关系，三角形的内角和定理，全等三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
如图，连接BF，OE.证明△OEF≌△OEB(SSS)，推出∠OFE=∠OBE，由OE=OB=OF，推出∠OEF=∠OFE=∠OEB=∠OBE，∠OFB=∠OBF，由∠ABF=12∠AOF=20°，推出∠OFB=∠OBE=20°，根据三角形内角和定理构建方程求出∠EFO即可．
【解答】
解：如图，连接BF，OE．
∵EF=EB，OE=OE，OF=OB，
∴△OEF≌△OEB(SSS)，
∴∠OFE=∠OBE，
∵OE=OB=OF，
∴∠OEF=∠OFE=∠OEB=∠OBE，∠OFB=∠OBF，
又∵∠OBF+∠OFB=2∠OBF=∠AOF，
∴∠ABF=12∠AOF=20°，
∴∠OFB=∠OBF=20°，
∵∠OFB+∠OBF+∠OFE+∠OBE+∠BEF=180°，
∴4∠EFO+40°=180°，
∴∠OFE=35°，
故选：D．
11.【答案】C
【解析】【分析】
本题考查圆心角、弧、弦的关系，平行线的性质，先根据AB，BC，CA三弧的度数比为12：13：11求出AB、BC、AC的度数，再根据其度数即可求出∠ACB及∠ABC的度数，由平行线的性质即可求出∠FED及∠EFD的度数，由三角形内角和定理即可求出∠EDF的度数．
【解答】
解：∵AB、BC、AC弧的度数比为12:13:11，
∴AB的度数为：1212+13+11×360∘=120∘，AC的度数为：1111+12+13×360∘=110∘，
∴∠ACB=12×120∘=60∘，∠ABC=12×110∘=55∘，
∵AC/​/ED，AB/​/DF，
∴∠FED=∠ACB=60∘，∠EFD=∠ABC=55∘，
∴∠EDF=180∘−60∘−55∘=65∘．
故选C．
12.【答案】A
【解析】解：如图，连接OC，当点M落在OB上时，CD⊥OB，
∵∠AOB=90°，AC=CB，
∴∠AOC=∠COB=45°，
∵CDO=90°，
∴∠DCO=∠COD=45°，
∴CD=OC=2 2．
当点M落在OA上时，连接CM，CB，CO，DM，过点C作CT⊥OB于点T，CJ⊥OA于点J，
∵∠CJO=∠JOT=∠OTC=90°，
∴四边形JOTC是矩形，
∵OT=TC，
∴四边形JOTC是正方形，
∴OJ=OT=CJ=CT=2 2，
∵CM=CN，CJ=CT，∠CJM=∠CTB=90°，
∴Rt△CJM≌Rt△CTB(HL)，
∴JM=TN=4−2 2，
设OD=y，则DM=DB=4−y．
∵OM2+OD2=DM2，
∴[2 2−(4−2 2)]2+y2=(4−y)2，
∴y=4 2−4，
观察图象可知：点M落在扇形OAB内(不含边界)，则4 2−4故选：A．
求出两种特殊位置：当点M落在OB上时，当点M落在OA上时，OD的值，可得结论．
本题考查圆心角，弧，弦，轴对称的性质，解直角三角形等知识，解题的关键是学会寻找特殊位置解决问题，属于中考常考题型．
13.【答案】42
【解析】解：如图，连接OC、OD，
∵AB=2DE，
∴OD=DE，
∴∠E=∠EOD=14∘，
在△EDO中，∠ODC=∠E+∠EOD=28∘，
∵OC=OD，
∴∠OCD=∠ODC=28∘，
在△CEO中，∠AOC=∠E+∠OCD=14∘+28∘=42∘，
∴弧AC的度数为42∘.
故答案为：42∘.
连接OC、OD，根据AB=2DE得DE等于圆的半径，在△EDO和△CEO中，根据三角形的一个外角等于和它不相邻的两个内角的和求出∠ODC，∠AOC，进而得到弧AC的度数．
本题考查了圆心角、弧、弦的关系，等腰三角形的性质，三角形外角的性质，求出∠AOC的度数是解题的关键．
14.【答案】2 2
【解析】如图，连接OA，∵AB⌢=AC⌢，
BC是直径，∴∠AOB=∠AOC=90°，即OA⊥BC，∵OA=OB，AB=2，∴在Rt△AOB中，AO2+BO2=AB2，∴OA=OB= 2，∴BC=2OB=2 2．
15.【答案】3
【解析】略
16.【答案】4 217
【解析】解：如图，连接OE.设OD=m．
∵CD⊥OB，
∴∠CDO=90°，
∵∠COD=60°，
∴∠OCD=90°−60°=30°，
∴OC=2OD=2m，
在Rt△OCD中，∵sin∠COD=CDOC，
∴CD=sin60°·2m
= 32·2m
= 3m，
∵△CDE是等边三角形，
∴CD=CE= 3m，∠DCE=60°，
∴∠OCE=∠OCD+∠DCE=90°，
∴OC2+CE2=OE2，
∴4m2+3m2=42，
∴m=4 77(负根已经舍去)，
∴CD= 3m=4 217．
故答案为：4 217．
如图，连接OE.设OD=m.证明∠OCE=90°，利用勾股定理构建方程求解即可．
本题考查解直角三角形，等边三角形的性质等知识，解题的关键是学会利用参数，构建方程解决问题，属于中考常考题型．
17.【答案】证明：∵AD=CB，
∴AD=BC，
∴AD+ AC=AC+BC，
即CD=AB，
∴AB=CD．
【解析】此题考查的是圆心角、弧、弦的关系，根据圆心角、弧、弦的关系定理结合已知条件证明CD=AB，再次根据圆心角、弧、弦的关系定理可得答案．
18.【答案】证明：连接AC，

∵PA=PC，
∴∠A=∠C，
∴BC=AD，
∴BC−BD=AD−BD，
∴CD=AB，
∴AB=CD．
【解析】连接AC，根据等腰三角形的性质可得∠A=∠C，从而可得BC=AD，然后利用等式的性质可得CD=AB，从而可得AB=CD，即可解答．
本题考查了圆心角、弧、弦的关系，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
19.【答案】证明(1)∵AB=CD，
∴AB=CD，即BC+AC=AD+AC，
∴AD=BC；
(2)∵AD=BC，
∴AD=CB，
在△ADE和△CBE中，
∠ADE=∠CBEAD=CB∠DAE=∠BCE,
∴△ADE≌△CBE(ASA)，
∴AE=CE．
【解析】本题主要考查圆心角、弧、弦的关系，圆心角、弧、弦三者的关系可理解为：在同圆或等圆中，①圆心角相等，②所对的弧相等，③所对的弦相等，三项“知一推二”，一项相等，其余二项皆相等；也考查了圆周角定理即在同圆或等圆中，同弧或等弧所对的圆周角相等．
(1)由AB=CD知AB=CD，即BC+AC=AD+AC，据此可得答案；
(2)由AD=BC知AD=CB，结合∠ADE=∠CBE，∠DAE=∠BCE可证△ADE≌△CBE(ASA)，从而得出答案．
20.【答案】(1)证明：∵∠AOD=∠BOE，
∴AD=BE．
∵AD=CE，
∴BE=CE，
∴BE=CE；
(2)解：∵∠B=50°，OB=OE，
∴∠BOE=180°−50°−50°=80°．
∵由(1)知，BE=CE，
∴∠COE=∠BOE=80°，
∴∠AOC=180°−80°−80°=20°．
【解析】本题主要考查的是圆心角，弧，弦的关系，等腰三角形的性质，三角形内角和定理．
(1)根据∠AOD=∠BOE可知AD=BE，再由AD=CE证出BE=CE，即可得出结论；
(2)先根据等腰三角形的性质求出∠BOE的度数，再由BE=CE可得出∠BOE=∠COE，根据邻补角的定义即可得出结论．
21.【答案】证明：∵AD=CB，
∴AD=CB，
∴AD+AC=CB+AC，
即CAD=ACB，
∴AB=CD．
【解析】根据圆心角、弧、弦之间的关系得出即可．
本题考查了圆心角、弧、弦之间的关系，能根据定理求出CAD=ACB是解此题的关键．
22.【答案】解：(1)如图①，连接AB，过点O、C作直线交⊙O于点M(OM⊥AB)，点M就是所求的点；
(2)如图②，连接BO，过点A作BO的垂线交⊙O于点N，BN即为所求．

【解析】(1)在图①中连接AB，过点O、C作直线交⊙O于点M(OM⊥AB)，点M就是所求的点；
(1)在图②中连接BO，过点A作BO的垂线交⊙O于点N，BN即为所求．
本题考查了作图−应用与设计作图，圆心角、弧、弦的关系，解决本题的关键是准确画图．
23.【答案】证明：如图，
∵AC=CB，
∴∠AOC=∠BOC，
∵CD⊥OA于D，CE⊥OB于E，
∴∠CDO=∠CEO=90°，
在△COD与△COE中，
∠DOC=∠EOC∠CDO=∠CEO=90°CO=CO,
∴△COD≌△COE(AAS)，
∴CD=CE．
【解析】本题考查的是圆心角，弧，弦的关系，全等三角形的判定与性质，熟知在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等是解答此题的关键．根据相等的弧所对的圆心角相等得到∠AOC=∠BOC，再根据CD⊥OA于D，CE⊥OB于E得出∠CDO=∠CEO=90°，然后证明△COD≌△COE，最后根据全等三角形的性质即可证明CD=CE．
24.【答案】解：(1)∵AB=2BC，
∴∠AOB=2∠BOC，
∵∠AOC=60°，
∴∠BOC=20°，∠AOB=40°，
∵OB=OC，
∴∠OBC=∠OCB=80°，
∵四边形OAFE是平行四边形，
∴OB/​/AF，
∴∠CFA=∠OBC=80°．
(2)连接AC，
∵OC=OA，∠AOC=60°，
∴△AOC是等边三角形，
∴∠OAC=60°，OC=AC，
∵四边形OAFE是平行四边形，
∴OE/​/AF，
∴∠OAF=180°−∠AOB=140°，
∴∠CAF=∠OAF−∠CAO=80°；
∴∠CAF=∠CFA=80°，
∴CA=CF，
∴CF=OC．
【解析】本题考查平行四边形的性质，圆心角，弧，弦之间的关系等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
(1)求出∠OBC=80°，再利用平行四边形的性质和平行线的性质求解即可．
(2)连接AC，则△AOC是等边三角形，可得∠OAC=60°，OC=AC，然后由平行线的性质和等角对等边证明CA=CF即可．
25.【答案】证明：如图，连接DE，BC．
∵AB=AC，
∴∠B=∠C，
∵∠ADE+∠EDB=180°，∠C+∠EDB=180°，
∴∠ADE=∠C，
同法可证，∠AED=∠B，
∴∠ADE=∠AED，
∴AD=AE，
∴BD=CE．
【解析】如图，连接DE，BC.证明∠ADE=∠AED，推出AD=AE，可得结论．
本题主要考查圆内接四边形的性质，等腰三角形的判定和性质，解题的关键是连接DE，BC，证明AD=AE．