初中数学人教版七年级下册5.2.2 平行线的判定课堂教学课件ppt

这是一份初中数学人教版七年级下册5.2.2 平行线的判定课堂教学课件ppt，共11页。PPT课件主要包含了学习目标，重难点，情景导入，教学过程，探究新知，例题精讲等内容，欢迎下载使用。
1.掌握平行线的三种判定方法.2.会运用这些判定方法解决问题.3.初步了解推理论证的方法，能正确书写简单的推理过程，逐步培养逻辑推理能力.
重点：探索两直线平行的条件.难点：两直线平行的条件的运用、会正确书写简单的推理过程.
装修工人正在向墙上钉木条，如果木条b与墙壁边缘垂直，那么木条a与墙壁边缘的夹角为多少度时，才能使木条a与木条b平行？
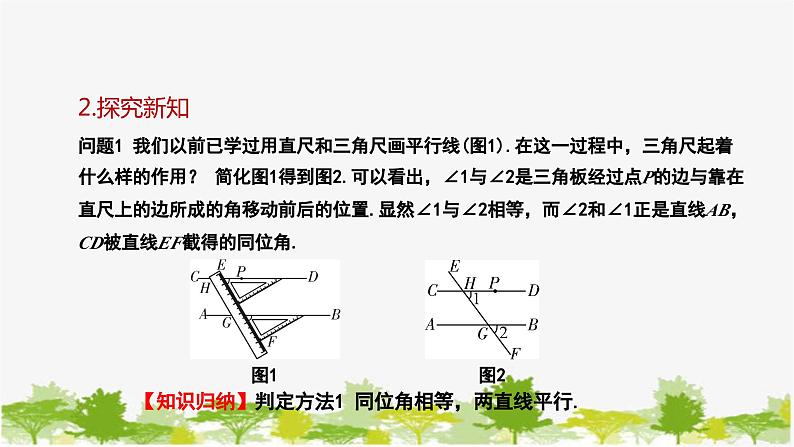
问题1 我们以前已学过用直尺和三角尺画平行线(图1).在这一过程中，三角尺起着什么样的作用？ 简化图1得到图2.可以看出，∠1与∠2是三角板经过点P的边与靠在直尺上的边所成的角移动前后的位置.显然∠1与∠2相等，而∠2和∠1正是直线AB，CD被直线EF截得的同位角. 图1 图2
【知识归纳】判定方法1 同位角相等，两直线平行.
问题2 两条直线被第三条直线所截，同时得到同位角、内错角和同旁内角.由同位角相等，可以判定两条直线平行，那么能否利用内错角，或同旁内角来判定两条直线平行呢?如图，（1）如果∠2=∠3，能得出a//b吗?（2）如果∠4+∠2=180°，能得出a//b吗？
（2）∵∠4+∠2=180°（已知），∠4+∠1=180°（已知），∴∠2=∠1（同角的补角相等），∴a∥b（同位角相等，两直线平行）
解：（1）∵∠2=∠3（已知），∠3=∠1（对顶角相等）.∴∠1=∠2 （等量代换），∴a∥b（同位角相等，两直线平行）
【知识归纳】判定方法2 内错角相等，两直线平行.判定方法3 同旁内角互补，两直线平行.
例1 在同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线平行吗?为什么?
解：这两条直线平行.理由如下:如图.∵b⊥a,∴∠1= 90°.同理 ∠2=90°，∴∠1=∠2.∵∠1和∠2是同位角，∴b∥c (同位 角相等，两直线平行).
【分析】垂直总与直角联系在一起，进而用判断两条直线平行的方法进行判定.
例2 如图,点B在DC上,BE平分∠ABD, ∠DBE=∠A，则BE∥AC,请说明理由.
解：∵BE平分∠ABD， ∴∠ABE=∠DBE(角平分线的定义). 又∵∠DBE=∠A，∠ABE=∠A(等量代换)， ∴ BE∥AC(内错角相等,两直线平行).
【分析】由BE平分∠ABD我们可以知道什么?联系∠DBE=∠A, 我们又可以知道什么?由此能得出BE//AC吗?为什么?
例3 如图，∠1=25°，∠B=65°，AB⊥AC.AD与BC有怎样的位置关系？为什么？
解：AD∥BC.理由如下: ∵∠1=25°，∠B=65°，AB⊥AC， ∴∠BAD=90°+25°=115°. ∵∠BAD+∠B=115°+65°= 180°， ∴AD∥BC.