初中数学人教版九年级上册21.2.3 因式分解法教学课件ppt

这是一份初中数学人教版九年级上册21.2.3 因式分解法教学课件ppt，共18页。PPT课件主要包含了x2aa≥0，直接开平方法，配方法，公式法，方法一配方法，方法二公式法，方法三因式分解法，4x2x等内容，欢迎下载使用。

学习目标1）利用因式分解法解一元二次方程。2）灵活运用各种方法解一元二次方程。重点运用因式分解法解一元二次方程。难点灵活运用各种方法解一元二次方程。
知识点回顾（一元二次方程的解法）
我们已经学过了几种解一元二次方程的方法?
(x+m)2=n (n≥0)
知识点回顾（多项式因式分解的方法）
① 提公因式法： pa+ pb + pc=p(a+b+c)
② 平方差公式： a2-b2=(a+b)(a-b)
③ 完全平方公式： a2±2ab+b2=(a±b)2
④ “十”字相乘法：x2+(p+q)x+pq = (x+p)(x+q)
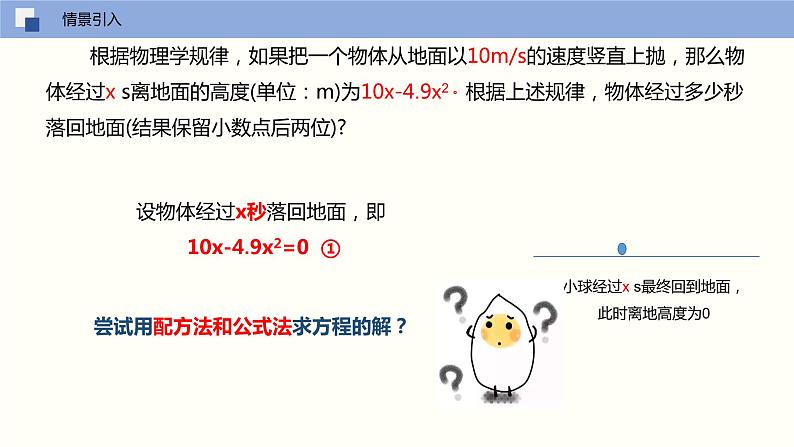
根据物理学规律，如果把一个物体从地面以10m/s的速度竖直上抛，那么物体经过x s离地面的高度(单位：m)为10x-4.9x2 。根据上述规律，物体经过多少秒落回地面(结果保留小数点后两位)?
小球经过x s最终回到地面，此时离地高度为0
设物体经过x秒落回地面，即 10x-4.9x2=0 ①
尝试用配方法和公式法求方程的解？
这两个根中，x2≈2.04表示物体约在2.04s落回地面，而x1=0表示物体被上抛离开地面的时刻，即在0s时物体被抛出，此刻物体的高度是0m.
本节我们探索用因式分解的方法求解一元二次方程
如果a×b=0，则a=_____或b=_______.
【思考】如何将10x-4.9x2=0变形为a×b=0
如果两个因式的积为0，那么这两个因式中至少有一个等于0；反之，如果两个因式中任何一个为0，那么它们的积也等于0。
解方程①时，二次方程是如何降为一次的?
先因式分解，使一元二次方程转化为两个一次式乘积等于0的形式，从而实现降次，这种解一元二次方程的方法叫做因式分解法。
10x-4.9x2=0
x(10-4.9x)=0
利用因式分解法求解一元二次方程的基本步骤
①移项，使一元二次方程等式右边为0;②分解，把左边运用因式分解法化为两个一次因式相乘的形式;③赋值，分别令每个因式等于0，得到两个一元一次方程;④求解，分别解这两个一元一次方程，得到方程的解。
归纳：左分解，右化零，两因式，各求解。
1) x1=0，x2=2；
(2) (x+2)(x-3)=0
2) x1=-2，x2=3 ；
(3) (3x+6)(2x-4)=0
3) x1=-2，x2=2；
4) x1=0，x2=1.
下列各方程的根分别是多少？
(1) x(x-2)=0
利用因式分解法解一元二次方程
1)解: 因式分解得 ，(x﹣2)(x+1)=0 于是得x-2=0，或x+1=0 ∴x1=2，x2=﹣1
2)解：移项、合并同类项，得4x2﹣1=0 因式分解，得 (2x+1)(2x-1)=0 ∴2x+1=0或2x﹣1=0 ∴x1=0.5，x2=﹣0.5
典例1 解下列方程：（3）x2+6x-7=0
解：因式分解得(x+7)(x-1)=0 ∴x+7=0或x-1=0 ∴x1=-7, x2=1
利用因式分解法求解一元二次方程
变式1-2 已知(x2+y2)(x2+y2-1)-6=0，则 x2+y2 的值是（ ）A．3或-2 B．-3或2C．3D．-2
解一元二次方程的基本思路
解一元二次方程的基本思路是：将二次方程化为一次方程，即降次。
选用合适的方法解一元二次方程
典例2① x2-3x+1=0 ； ② 3x2-1=0 ； ③ -3t2+t=0 ； ④ x2-4x=2 ； ⑤ 2x2-x=0； ⑥ 5(m+2)2=8；⑦ 3y2-y-1=0； ⑧ 2x2+4x-1=0；⑨ (x-2)2=2(x-2).1）适合运用直接开平方法 ；2）适合运用因式分解法 ；3）适合运用公式法 ；4）适合运用配方法 . 【提示】每个题都有多种解法，选择更合适的方法，可以简化解题过程！