人教版九年级上册22.3 实际问题与二次函数教学课件ppt

这是一份人教版九年级上册22.3 实际问题与二次函数教学课件ppt，共18页。PPT课件主要包含了数学问题，数学知识，解决问题，实际问题，矩形区域，-4x等内容，欢迎下载使用。

学习目标1）根据实际问题，找出变量之间存在的关系，列出函数关系式并确定自变量的取值范围。2）通过二次函数顶点公式求实际问题中的极值。重点列出二次函数关系式，并确定自变量的取值范围。难点通过二次函数顶点公式求实际问题中的极值。
【分析】画出函数的图像h=30t-5t2（0≤t≤6），可以看出这个函数图象是一条抛物线的一部分。而我们已知二次函数与对称轴的交点，可以得到二次函数的最大值（或最小值）。
小球运动的时间是 3 s 时，小球最高．最大高度是 45 m．
例1 从地面竖直向上抛出一小球，小球的高度 h（单位：m）与小球的运动时间 t（单位：s）之间的关系式是h=30t-5t2（0≤t≤6）．小球的运动时间是多少时，小球最高？小球运动中的最大高度是多少？
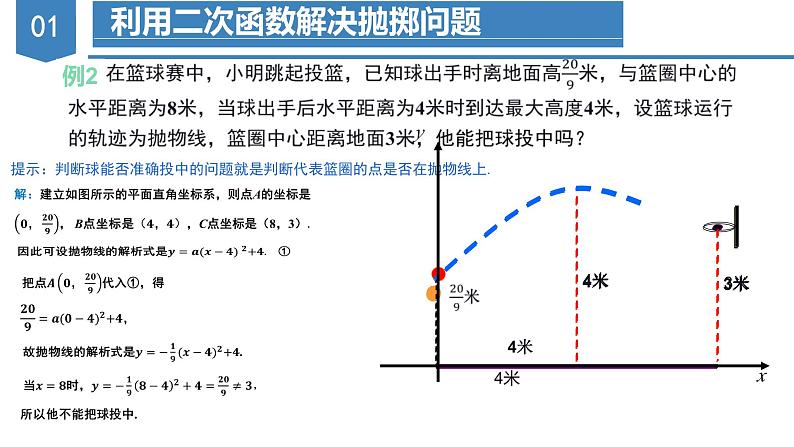
提示：判断球能否准确投中的问题就是判断代表篮圈的点是否在抛物线上.
运用二次函数知识解决实际问题的步骤：1.分析题意，把实际问题转化为数学问题，画出图形.2.根据已知条件建立适当的平面直角坐标系.3.选用适当的函数解析式求解.4.根据二次函数的解析式解决具体的实际问题.
（二次函数解决抛掷问题）
例题2 把一个足球垂直地面向上踢，t（秒）后该足球的高度h（米）适用公式h＝20t-5t2．（1）经多少秒后足球回到地面？（2）圆圆说足球的高度能达到21米，方方说足球的高度能达到20米．你认为圆圆和方方的说法对吗？为什么？
1）解：当h＝0时，20t−5t2＝0，解得：t＝0或t＝4，答：经4秒后足球回到地面；
2）方方的说法对，理由：将h＝21代入公式得：21＝20t−5t2，移项得5t2−20t＋21＝0，由判别式计算可知：△＝（−20）2−4×5×21＝−20＜0，此方程无解；将h＝20代入公式得：20＝20t−5t2，解得：t＝2，∴足球确实无法到达21米的高度，能达到20米，故方方的说法对．
例题3 足球运动员将足球沿与地面成一定角度的方向踢出，足球飞行的路线是一条抛物线. 不考虑空气阻力，足球距离地面的高度h（单位：m）与足球被踢出后经过的时间t（单位：s）之间的关系如下表： 下列结论：①足球距离地面的最大高度为20m；②足球飞行路线的对称轴是直线t=4.5 ；③足球被踢出9s时落地；④足球被踢出1.5s时，距离地面的高度是11m. 其中正确结论的个数是（ ）A．1B．2C．3D．4
【详解】解：由题意，抛物线的解析式为y=ax（x﹣9），把（1，8）代入可得a=﹣1，∴y=﹣t2+9t=﹣（t﹣4.5）2+20.25，∴足球距离地面的最大高度为20.25m，故①错误，∴抛物线的对称轴t=4.5，故②正确，∵t=9时，y=0，∴足球被踢出9s时落地，故③正确，∵t=1.5时，y=11.25，故④错误，∴正确的有②③，故选B．
例3 用总长为60m的篱笆围成矩形场地，矩形面积S随矩形一边长x的变化而变化。当x是多少时，场地的面积S最大，最大面积是多少？
例4 如图，用一段长为60 m的篱笆围成一个一边靠墙的矩形菜园，墙长18 m，这个矩形的长、宽各为多少时，菜园的面积最大？最大面积是多少?
实际问题中求解二次函数最值问题时，函数的最值要考虑自变量的取值范围：1）当自变量的取值包含顶点时，函数的最值在函数的顶点处取得；2）当自变量的取值不包含顶点时，函数的最值一般在端点处取得，此时要考虑函数的增减性。
例5 如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米。(1)求S与x的函数关系式及自变量的取值范围；(2)当x取何值时所围成的花圃面积最大，最大值是多少？(3)若墙的最大可用长度为8米，则求围成花圃的最大面积。
1）S＝x（24－4x）＝－4x2＋24x（03) ∵墙的可用长度为8米∴ 0<24－4x ≤8 ∴ 4≤x<6∴当x＝4cm时，S最大值＝32 平方米
（二次函数解决几何图形最值问题）
例题2 用一条长为40cm的绳子围成一个面积为S的长方形，S的值不可能为(　　)A．20 B．40 C．100 D．120
例题3 用长为6m的铝合金型材做一个形状如图所示的矩形窗框，要使做成的窗框的透光面积最大，则该窗的长，宽应分别是多少？
用二次函数解决实际问题的一般步骤：
1.审：仔细审题，厘清题意；2.设：找出题中的变量和常量，分析它们之间的关系，与图形相关的问题要结合图形具体分析，设出适当的未知数；3.列：用二次函数表示出变量和常量之间的关系，建立二次函数模型，写出二次函数的解析式；4.解：依据已知条件，借助二次函数的解析式、图象和性质等求解实际问题；5.检：检验结果，进行合理取舍，得出符合实际意义的结论.