初中数学人教版九年级上册24.1.2 垂直于弦的直径教学ppt课件

这是一份初中数学人教版九年级上册24.1.2 垂直于弦的直径教学ppt课件，共22页。PPT课件主要包含了轴对称图形概念，CEDE，符号语言，情况一弦是直径，情况二弦不是直径，不一定等内容，欢迎下载使用。

学习目标1) 理解圆的轴对称性及垂径定理的推导，能初步应用垂径定理进行计算和证明；2) 通过圆的对称性，培养学生对数学的审美观，并激发学生对数学的热爱。重点理解垂径定理的推导。难点利用垂径定理解决实际问题。
如果一个图形沿一条直线对折，直线两旁的部分能够互相重合，那么这个图形叫轴对称图形。
常见的轴对称图形图形：
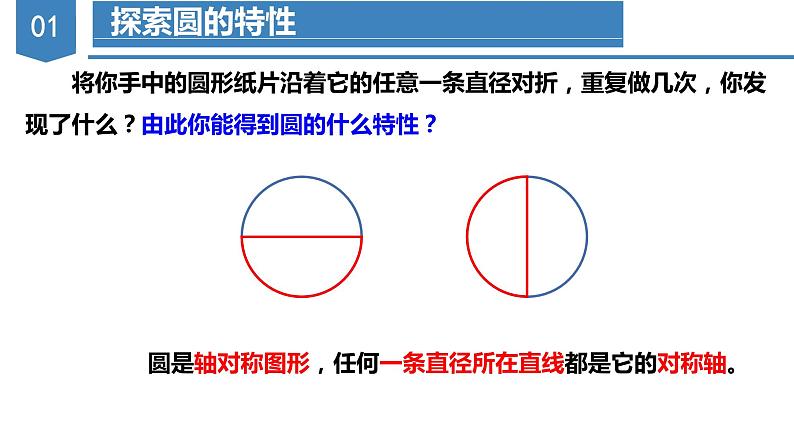
将你手中的圆形纸片沿着它的任意一条直径对折，重复做几次，你发现了什么？由此你能得到圆的什么特性？
圆是轴对称图形，任何一条直径所在直线都是它的对称轴。
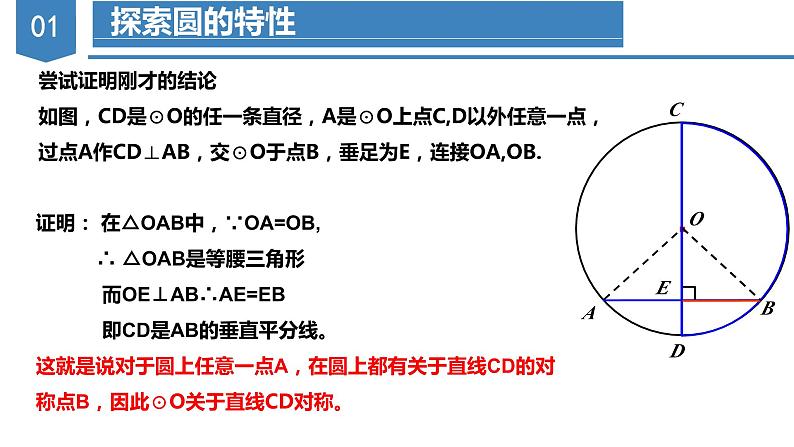
尝试证明刚才的结论如图，CD是⊙O的任一条直径，A是⊙O上点C,D以外任意一点，过点A作CD⊥AB，交⊙O于点B，垂足为E，连接OA,OB.
证明： 在△OAB中，∵OA=OB, ∴ △OAB是等腰三角形 而OE⊥AB∴AE=EB 即CD是AB的垂直平分线。这就是说对于圆上任意一点A，在圆上都有关于直线CD的对称点B，因此⊙O关于直线CD对称。
根据轴对称图形性质，你能发现图中有那些相等的线段和弧？并尝试证明？
证明：连接OC、OD,在△OCD中，∵OC=OD，且OE⊥CD,∴CE=DE，∠COB=∠BOD,∴ ∠AOC=∠AOD,
垂直于弦的直径平分弦，并且平分弦所对的两条弧。
∵ CD是直径， CD⊥AB
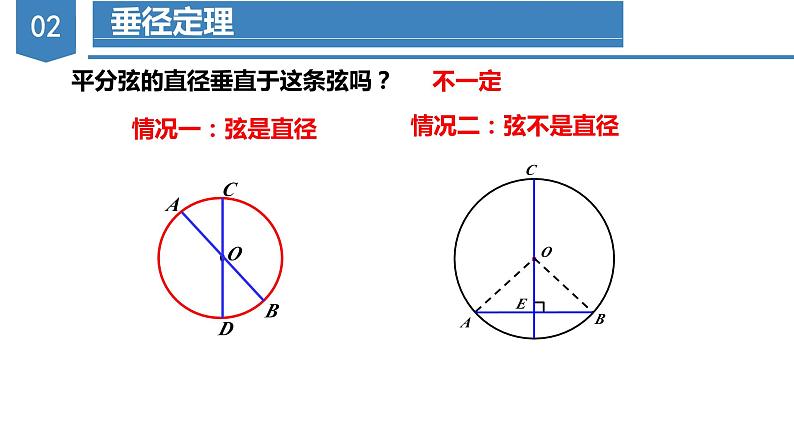
平分弦的直径垂直于这条弦吗？
判断下列图形，能否使用垂径定理？
平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。
∵ CD是直径 ， AE=BE且AB不是直径
弦心距：圆心到弦的距离（即圆心到弦的垂线段的距离）．
（利用垂径定理进行计算）
如图，在⊙O中，弦AB的长为 6 cm，圆心O到AB的距离（弦心距）为 4 cm，求⊙O的半径．
变式1 如图，在ʘO中，AB=8，OA=5， 则OE= ，ED= ．
变式2：如图，在ʘO中，OA=5，ED=2， 则OE= ，AB= .
变式3：如图，在ʘO中，AB=8，ED=2， 则OA= ，OE= .
r2 = (r － 2)2 + 42
半径、弦长、弦心距、弓形高四个量中，知二求二
变式4：如图，⊙M 与x轴交于A，B 两点，与y轴交于C，D 两点，若M(2,0)，B(5,0)，则C点的坐标是 .
变式5：如图，⊙O 的直径CD⊥AB于E，AB＝6cm，CE＝9㎝.求⊙O 的半径.
（利用垂径定理解决实际问题）
1400多年前,我国隋朝建的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37 m,拱高为7.23m,求桥拱的半径(精确到0.1m).
【解题关键】将实际问题转化为几何问题。
1400多年前,我国隋朝建的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为 37m,拱高为7.23m,求桥拱的半径(精确到0.1m).
思路：通过垂径定理，构造直角三角形，结合勾股定理，建立方程。
如图是一个圆弧形门拱，拱高1m ，跨度4m ，那么这个门拱的半径为（ ）A.2m C.3m D.5m
【详解】设这个门拱的半径为r，则OB=r−1，∵CD=4m，AB⊥CD，∴BC= CD=2m，在Rt△BOC中，∵BC2+OB2 =OC2 ,即22 +(r−1) 2 =r 2，解得r=2.5m.故选B.
如图，石拱桥的桥顶到水面的距离CD为8m，桥拱半径OC为5m，则水面AB宽为（　　）A.4m B.5m C.6m D.8m
本节课你学习了关于圆的哪些数学知识？
你掌握了哪些常用的辅助线作法和解题方法？
2.圆心到弦的距离、半径、半弦构成直角三角形，便将问题转化为直角三角形解决.
1.关于弦的问题，常常需要过圆心作弦的垂线段，连接半径等重要的辅助线.
3.半径、弦长、弦心距、弓形高中，知二求二.