初中24.1.3 弧、弦、圆心角教学ppt课件

这是一份初中24.1.3 弧、弦、圆心角教学ppt课件，共21页。PPT课件主要包含了旋转60°，旋转90°，旋转120°，∠BOC，不是顶点不在圆心，ABCD等内容，欢迎下载使用。
学习目标1）经过观察、讨论、发现圆的旋转不变性和中心对称性。2）经过观察、讨论、推理了解圆心角、弧、弦之间的关系。重点理解圆心角、弧、弦之间的关系。难点利用圆心角、弧、弦之间的关系进行计算。
问题1：圆是中心对称图形吗？它的对称中心在哪里？问题2：把圆绕着圆心旋转一个任意角度，旋转之后的图形还能与原图形重合吗？
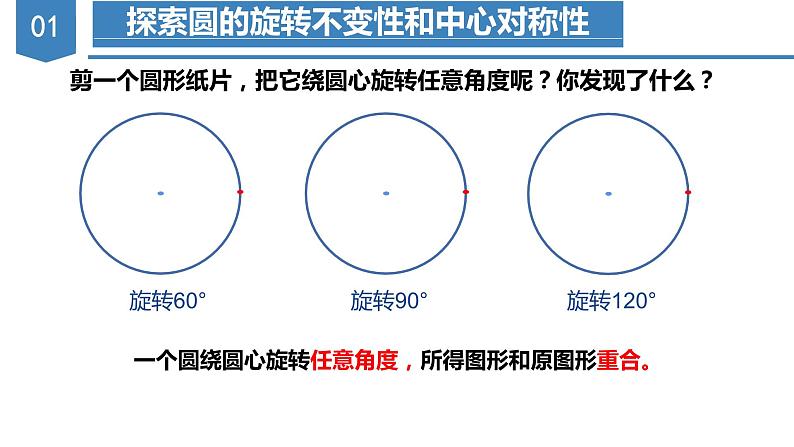
剪一个圆形纸片，把它绕圆心旋转任意角度呢？你发现了什么？
一个圆绕圆心旋转任意角度，所得图形和原图形重合。
剪一个圆形纸片，把它绕圆心旋转180°，所得的图形与原图形重合吗？由此你能得到什么结论？
圆是中心对称图形，圆心就是它的对称中心。
圆心角的定义：顶点在圆心的角叫做圆心角。圆心角的判断方法：观察顶点是否在圆心。　　　　　　　　　　　　　　
问题一 找出⊙Ｏ中的圆心角？问题二：∠ABC是不是圆心角？并说明原因？
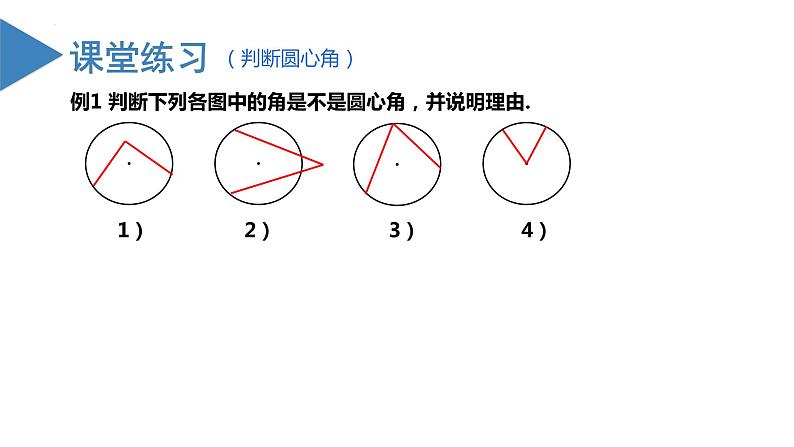
例1 判断下列各图中的角是不是圆心角，并说明理由. 1） 2） 3） 4）
问题一 任意圆心角，对应出现三个量：问题二 这三个量之间会有什么关系呢？
本节课我们探究探究弧、弦、圆心角之间的关系
如图，将圆心角∠AOB绕圆心O旋转到∠A1OB1的位置，你能发现哪些等量关系？为什么？
如图，在等圆中，如果∠AOB＝∠A'O'B'，你发现的等量关系是否依然成立？为什么？
由∠AOB＝∠A'O'B'得到
在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等。
在同圆或等圆中，两条弧相等，则他们所对应的其余各组量有什么关系？
在同圆或等圆中，相等的弧所对的圆心角相等，所对的弦相等
在同圆或等圆中，两条弦相等，则他们所对应的其余各组量有什么关系？
在同圆或等圆中，相等的弦所对的圆心角相等，所对优弧和劣弧分别相等
在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对的其余各组量都分别相等。
【问题】“同圆或等圆”的条件能少吗？
不能少，理由：如图下图，已知∠COD= ∠AOB但是线段CD不等于线段AB ，弧CD也不等于弧AB。
（考查弧、弦、圆心角之间的关系的关系）
∵AB=CD，∴∠AOB=∠COD．∵ AO=CO，BO=DO，则△AOB ≌ △COD．而OE 、OF 是 AB 与 CD 对应边上的高，∴OE=OF．
变式2-1 如图，AB是⊙O的直径，BC=CD=DE,∠AOE=66°，则∠COD的度数是( )A．108° B．72° C．48° D．38°变式2-2 如图，已知AB是⊙O的直径，C、D是半圆上两个三等分点，则∠COD= .变式2-3 如图，在⊙O中，点C是AB的中点，∠A=70°，则∠BOC=________________
变式2-6 已知：如图，在⊙O中，弦AB和CD相交，连接AC、BD，且AC＝BD． 求证：AB＝CD．
如图，若∠AOB=2∠COD，则有AB=2CD ， AB=2CD，你觉得这个结论正确吗？说明理由 。
连接AE,BE∵ ∠AOE=∠EOB=∠COD，∴ AE=BE=CD， ∴2CD=AE+BE而AB＜AE+BE，即AB＜2CD∴AB=2CD不成立