高中物理第八章 机械能守恒定律4 机械能守恒定律授课课件ppt

这是一份高中物理第八章 机械能守恒定律4 机械能守恒定律授课课件ppt，共26页。PPT课件主要包含了课堂练习等内容，欢迎下载使用。

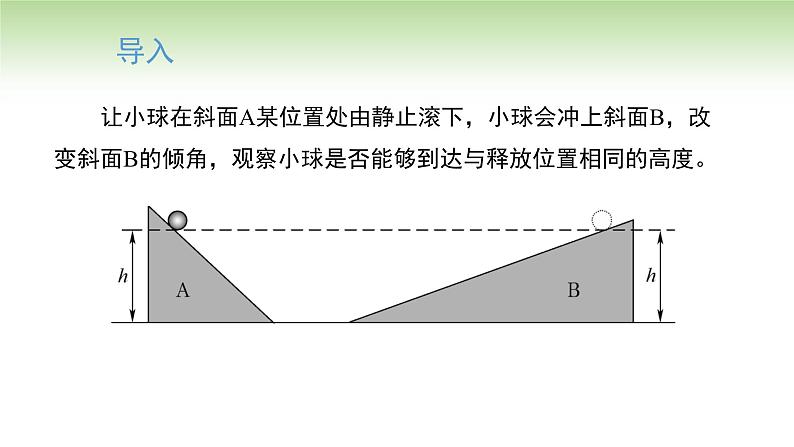
　　让小球在斜面A某位置处由静止滚下，小球会冲上斜面B，改变斜面B的倾角，观察小球是否能够到达与释放位置相同的高度。
　　伽利略曾研究过小球在斜面上的运动。改变斜面A的倾角，小球的速度最后总会在斜面B上的某位置变为0，那小球能否到达与释放位置相同的高度呢？　　不能。因为存在空气阻力和摩擦力。　　如果空气阻力和摩擦力小到可以忽略不计，又会出现什么现象呢？　　小球在斜面B上静止时，距底面的竖直高度与它出发时的竖直高度基本相同。
环节一：分析“斜面实验”，初步认识守恒思想
　　小球似乎会“记住”或“有愿望”，总想回到原来的高度。某种“东西”在小球的运动过程中是不变的。运动过程中总是保持不变的量，我们称之为“守恒量”。在忽略空气阻力和摩擦力影响的前提下，小球在斜面A、B上运动的过程中什么量是守恒的呢？　　能量守恒。　　16世纪末，伽利略、惠更斯、托马斯·杨等科学家对上述现象进行了不懈的研究，认为应当从能量的角度来研究这个“守恒量”。这节课我们就从能量的角度来研究一下，能量是如何转化的呢？这个关于能量的守恒量究竟是什么呢？
　　在忽略空气阻力和摩擦力的前提下，我们可以把两个斜面抽象成光滑斜面。请大家从能量的角度来认识这个物理过程——小球从斜面A上由静止滚下到冲上斜面B且速度变为0的过程中，哪些能量发生了转化？　　小球从光滑斜面A上滚下的过程中，它的重力势能不断减少，但它的速度越来越大，即它的动能不断增加，所以这个过程中小球的重力势能转化为动能；在小球冲上光滑斜面B的过程中，它的重力势能不断增加，但它的速度越来越小，即它的动能不断减少，在这个过程中小球的动能不断转化为重力势能。
环节二：从动能和势能转化的角度，认识机械　　　　能守恒
　　做功是能量转化的量度，在整个过程中，通过什么力做功使重力势能发生了变化？通过什么力做功使动能发生了变化？　　小球从光滑斜面A滚下的过程中，重力做正功，重力势能减少；小球冲上光滑斜面B的过程中，重力做负功，重力势能增加。整个过程中，只有重力做了功。小球从光滑斜面A上滚下的过程中，重力做正功，动能增加；小球冲上光滑斜面B的过程中，重力做负功，动能减少。
　　通过重力做功，重力势能和动能之间发生了转化。在整个过程中，什么是守恒量?　　重力势能和动能之和保持不变，所以重力势能和动能之和是守恒量。　　弹性势能可以与动能相互转化吗？
　　在水平桌面上放置一个气垫导轨，将弹簧的一端固定于气垫导轨左侧，弹簧的另一端与滑块相连。开始，弹簧处于原长状态，滑块位于O点。然后，推动滑块压缩弹簧至某一位置A并由静止释放，滑块来回振动。　　在这个过程中，空气阻力和摩擦力足够小，可以忽略不计。滑块的运动有什么特点？　　滑块在O点左右两侧运动。
　　在理想过程中，能量是如何转化的？通过什么力做功，实现了能量的转化？整个过程中，存在守恒量吗？　　从A点到O点，弹力做正功，弹性势能减少。根据动能定理，只有弹力做功，合力做的功即弹力做的功，弹力做正功，动能增加。滑块到达O点时，动能最大，弹性势能最小。　　从O点到B点，弹力做负功，弹性势能增加。根据动能定理，只有弹力做功，合力做的功即弹力做的功，弹力做负功，动能减少。滑块到达B点时，动能最小，弹性势能最大。　　整个过程中，通过弹力做功，弹性势能和动能之间相互转化，弹性势能和动能之和保持不变。
　　如图所示，一个小球在真空中做自由落体运动，另一个同样的小球在黏性较大的液体中由静止开始下落。它们都由高度为h1的地方下落到高度为h2的地方。在这两种情况下，重力做的功相等吗？重力势能的变化相等吗？动能的变化相等吗？重力势能各转化成什么形式的能？
　　这两种情况下，重力做的功相同，重力做的功等于重力势能的变化量，所以重力势能的变化相等。动能的变化可以根据动能定理来分析。在真空中，重力做的功等于动能的变化量，减少的重力势能等于增加的动能，系统机械能守恒。在黏性较大的液体中，重力做的功和阻力做的功之和等于动能的变化量，减少的重力势能一部分转化为动能，一部分转化为内能，系统机械能不守恒。
　　请同学们试着举例，还有哪些过程中系统机械能守恒？　　竖直上抛小钢球，小钢球受到的空气阻力较小，可以忽略不计。在这个过程中，只有重力做功，系统机械能守恒。
　　动能与势能之间的相互转化，是否存在定量关系呢？　　如图所示，质量为m的物体沿光滑的曲面下滑，下落过程中经过任意两个位置A和B，高度由h1变化到h2，速度由v1变化到v2，不计空气阻力。请利用动能定理和重力做功的特点，讨论沿光滑曲面下滑的物块的机械能是否守恒。
环节三：通过定量研究机械能之间的相互转化，　　　　得出机械能守恒定律
　　上述过程中，物体从位置B上升到位置A的过程中，重力做负功，上述关系式是否依然成立？　　重力虽然做负功，但是合力做的功与动能的关系、重力做功与重力势能的关系依然成立，因此上述关系式也仍然是成立的。
　　在水平弹簧系统中，可以定量分析动能和弹性势能的相互转化吗？　　在水平弹簧系统中，只有弹力做功。根据动能定理，弹力对物体做的功等于物体动能的增加量，弹力对物体做的功等于弹性势能的减少量。也可以定量分析出，系统内只有动能和弹性势能相互转化时，系统的机械能守恒。
　　如果在一个过程中，重力和弹力都做功，系统的机械能还守恒吗？　　例题　竖直悬挂的轻弹簧下连接一个小球，小球处于静止状态时位于O点。用手托起小球至某位置。放手后，小球来回振动。忽略空气阻力的影响，在小球振动的过程中，系统机械能守恒吗？为什么？
　　在小球运动的过程中，任选两个状态A和B。选某位置为势能零点，处于状态A时，物体具有的动能为EkA，系统具有的重力势能为Ep重A，系统具有的弹性势能为Ep弹A；处于状态B时，物体具有动能为EkB，系统具有的重力势能为Ep重B，系统具有的弹性势能为Ep弹B。
　　在只有重力或弹力做功的物体系统内，动能与势能可以相互转化，而总的机械能保持不变，这叫作机械能守恒定律。　　根据以上的研究，你认为物体在运动过程中机械能守恒的条件是什么？你对机械能守恒是如何理解的？　　只有重力或弹力做功。
　　重力势能是地球与物体所组成的“系统”所共有的，弹性势能也是系统所共有的，如弹簧的弹性势能是弹簧与弹簧连接的物体所构成的“系统”所共有的，它们都具有系统性，所以守恒对象是指“系统”。　　对“只有重力或弹力做功”的守恒条件的理解，弹力指的是系统内的弹力，守恒条件可以理解为在系统内有且仅有重力或系统内的弹力做功。　　“动能与势能相互转化”是指系统内不同形式的机械能相互转化，其他形式的能量不参与该转化。
　　例题　把一小球用细线悬挂起来，就成为一个摆，摆长为l，最大偏角为θ。如果阻力可以忽略，小球运动到最低点时的速度大小是多少？
环节四：机械能守恒定律的应用
　　应用机械能守恒定律分析问题的思维流程：　　(1)确定研究对象及运动过程。　　(2)分析物体在运动过程中的受力情况，明确过程中系统内是否只有重力或弹力做功，是否满足机械能守恒的条件。　　(3)如果满足机械能守恒的条件，规定势能参考面，明确初状态的动能和势能和末状态的动能和势能。　　(4)根据机械能守恒定律写出表达式并计算求解。