华东师大版数学七年级下册 9.2 第2课时 多边形的外角和 课件

这是一份华东师大版数学七年级下册 9.2 第2课时 多边形的外角和 课件，共13页。

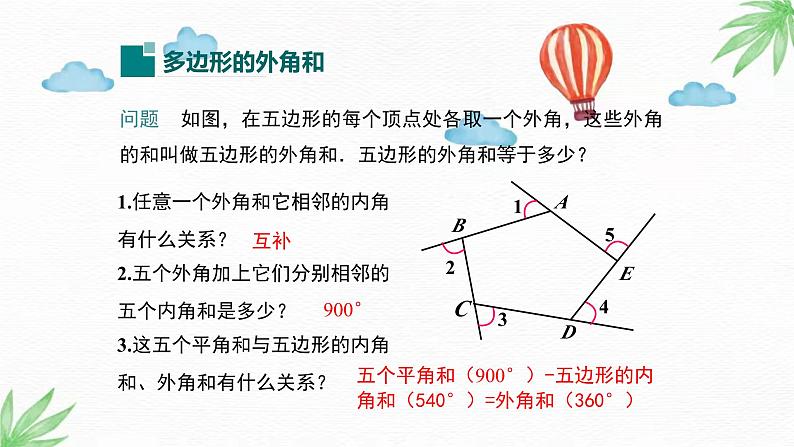
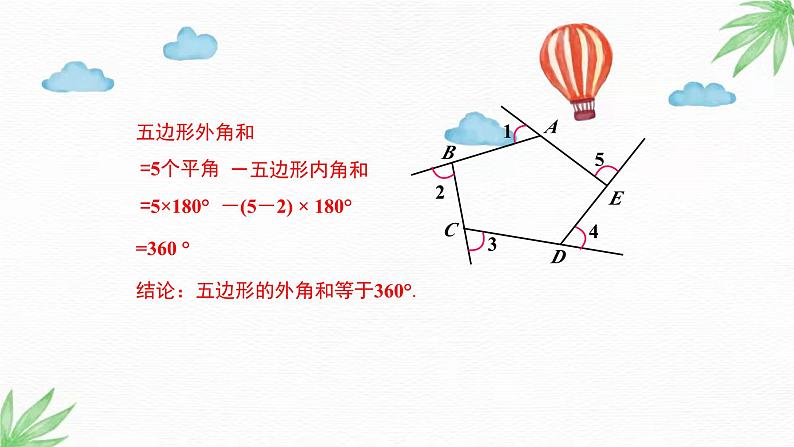
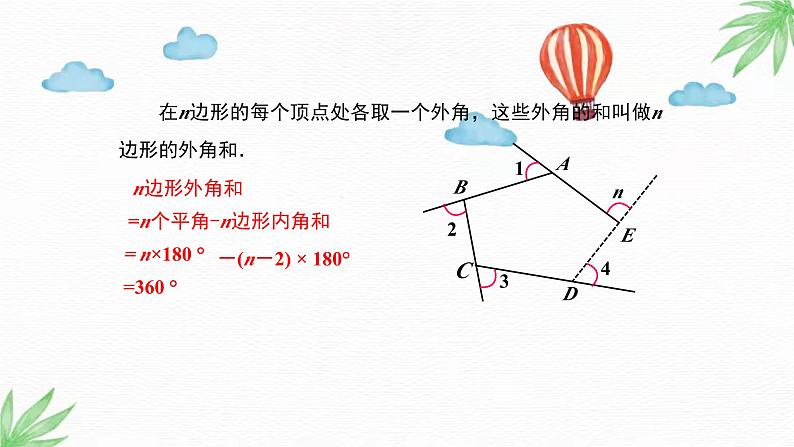
导入新课讲授新课当堂练习课堂小结9.2 多边形的内角和与外角和第2课时 多边形的外角和 情境引入1.掌握多边形外角和的推导.2.运用多边形的外角和解决问题.（重点）情境引入 清晨，小明沿一个五边形广场周围的小路，按逆时针方向跑步。他每跑完一圈，身体转过的角度之和是多少度？问题 如图，在五边形的每个顶点处各取一个外角，这些外角的和叫做五边形的外角和．五边形的外角和等于多少？1.任意一个外角和它相邻的内角有什么关系？2.五个外角加上它们分别相邻的五个内角和是多少？3.这五个平角和与五边形的内角和、外角和有什么关系？互补900°五个平角和（900°）-五边形的内角和（540°）=外角和（360°）五边形外角和=360 °=5个平角－五边形内角和=5×180°－(5－2) × 180°结论：五边形的外角和等于360°. 在n边形的每个顶点处各取一个外角，这些外角的和叫做n边形的外角和．n边形外角和－(n－2) × 180°=360 °=n个平角-n边形内角和= n×180 °任意多边形的外角和等于360°.归纳总结例1 已知一个多边形，它的内角和等于外角和的5倍，求这个多边形的边数.解： 设多边形的边数为n. ∵它的内角和等于 (n－2)•180°， 多边形外角和等于360°， ∴ (n－2)•180°=5× 360º. 解得 n=12. ∴这个多边形的边数为12.12例2 已知一个多边形的每个内角与外角的比都是7:2，求这个多边形的边数.解：设这个多边形的内角为7x °,外角为2x°,根据题意得7x+2x=180，解得x=20.即每个内角是140 °，每个外角是40 °.360° ÷40 °=9.答：这个多边形是九边形.还有其他解法吗？解：设这个多边形的边数为x ,根据题意得解得x=9.答：这个多边形是九边形.1.判断．（1）当多边形边数增加时，它的外角和也随着增加． ( )（2）三角形的外角和与八边形的外角和相等． ( ) 2. 一个多边形所有内角与一个外角的和是2380°，则这个多边形的边数为___.15解析：设这个多边形的边数为x(x为正整数)，则这个多边形的内角和为（x-2）×180°，由题意可得：2380-180<（x-2）×180°<2380,解得：4.22