数学八年级下册2 平行四边形的判定教学ppt课件

这是一份数学八年级下册2 平行四边形的判定教学ppt课件，文件包含北师大版数学八年级下册62平行四边形的判定第1课时同步课件pptx、北师大版数学八年级下册62平行四边形的判定第1课时教学设计含教学反思docx等2份课件配套教学资源，其中PPT共26页， 欢迎下载使用。

1、探索并证明平行四边形的判定定理1、判定定理2；2、理解平行四边形的判定定理1、判定定理2，并会简单运用；3、在运用平行四边形的判定方法解决问题的过程中，进一步培养和发展逻辑思维能力和推理论证的表达能力．
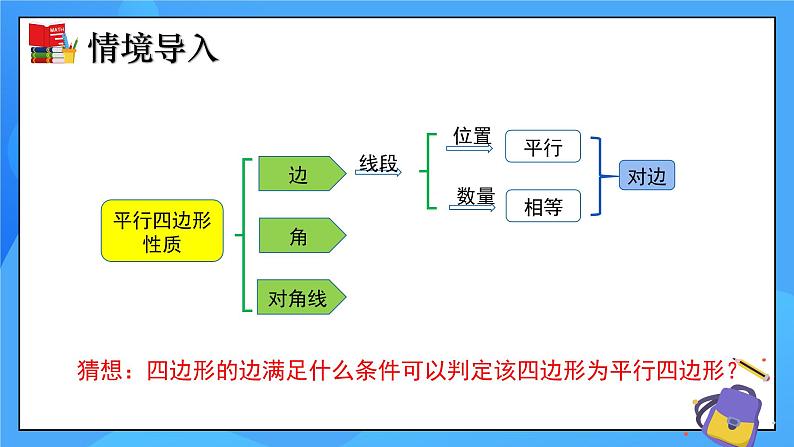
猜想：四边形的边满足什么条件可以判定该四边形为平行四边形？
周末，小明的爸爸带着他回到了老家，看望乡下的爷爷.午饭后，小明的爷爷准备给他心爱的小菜园扎篱笆，地上散落着很多长短不一的细木棒.这时小明的爸爸说：“小明，你们现在已经开始学习平行四边形了，你能不能挑四根细木棒拼一个平行四边形呢？”
(2)他怎样才能拼接成平行四边形？为什么？
你能为小明出谋划策吗？
(1)他应该选什么规格的细木棒？
平行四边形的判定定理1
上面的问题实际就是一个平行四边形的判定问题.你首先想到的是用什么来判定？
用平行四边形的定义来判定，只要能说明四边形的两组对边是平行的，就可以证明木工师傅锯的木板是平行四边形.
定义判定：两组对边分别平行的四边形是平行四边形.
定义判定是一切判定的基础.
对平行四边形的判定，除了用定义判定，我们常常用平行四边形的性质来判定.
我们知道：平行四边形的两组对边相等.
反过来：两组对边分别相等的四边形是平行四边形吗？
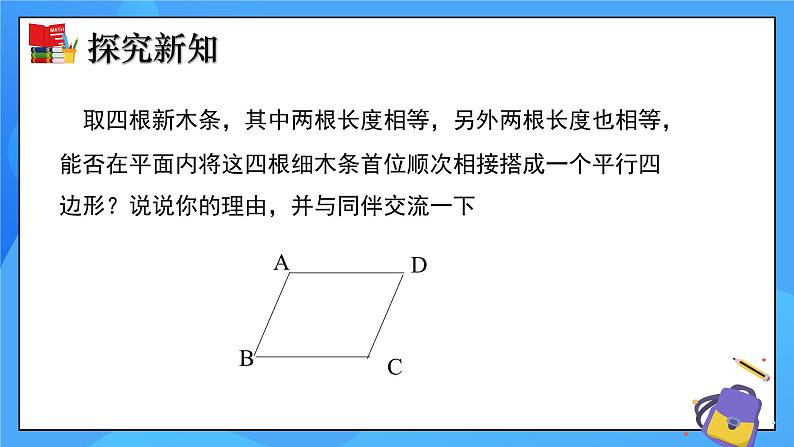
取四根新木条，其中两根长度相等，另外两根长度也相等，能否在平面内将这四根细木条首位顺次相接搭成一个平行四边形？说说你的理由，并与同伴交流一下
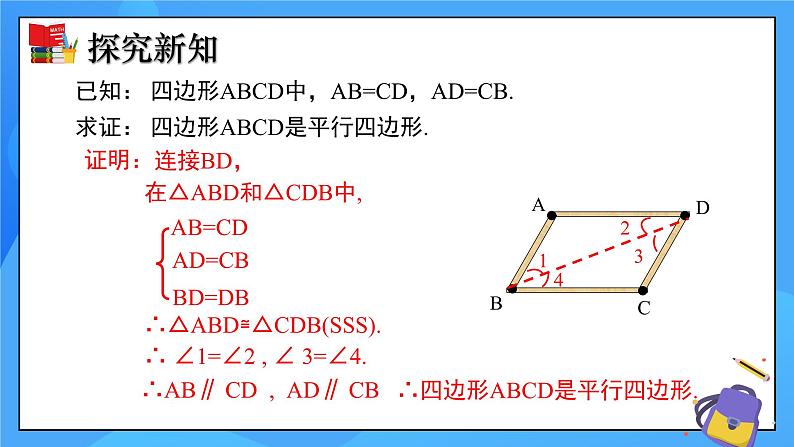
已知： 四边形ABCD中，AB=CD，AD=CB.求证： 四边形ABCD是平行四边形.
在△ABD和△CDB中,
∴△ABD≌△CDB(SSS).
∴ ∠1=∠2 , ∠ 3=∠4.
∴AB∥ CD , AD∥ CB
∴四边形ABCD是平行四边形.
两组对边分别相等的四边形是平行四边形.
几何语言描述：在四边形ABCD中，∵AB=CD,AD=BC,∴四边形ABCD是平行四边形.
平行四边形的判定定理1：
例：如图，在Rt△MON中，∠MON＝90°.求证：四边形PONM是平行四边形．
证明：Rt△MON中，由勾股定理得(x－5)2＋42＝(x－3)2， 解得x＝8.∴PM＝11－x＝3，ON＝x－5＝3，MN＝x－3＝5.∴PM＝ON，OP＝MN，∴四边形PONM是平行四边形．
小明的爸爸又考验小明：“小明啊，如果只用两根相等的细木棒，你能不能摆成细木棒的四个端点恰好是一个平行四边形的四个顶点呢？”
（2）如果四边形有一组对边相等，那么还需要添加什么条件，才能使它成为平行四边形？
（1）你认为小明能做到吗？
猜想：一组对边平行且相等的四边形是平行四边形
如图，在四边形ABCD中，AB∥CD，且AB＝CD．求证：四边形ABCD是平行四边形．
证明：如图，连接AC．∵AB∥CD，∴∠BAC＝∠ACD，又∵ AB＝CD，AC＝CA，∴ △BAC≌△DCA，∴ BC＝AD．∴ 四边形ABCD是平行四边形．
平行四边形的判定定理2：
一组对边平行且相等的四边形是平行四边形.
几何语言描述：在四边形ABCD中，∵AB CD，∴四边形ABCD是平行四边形.
例： 如图，在▱ABCD中，E，F分别是AB，CD的中点.求证：四边形EBFD是平行四边形.
1．能判定四边形ABCD为平行四边形的题设是（ ） A．AB∥CD，AD＝BC B．AB＝CD，AD＝BC C．∠A＝∠B，∠C＝∠D D．AB＝AD，CB＝CD
2．下列叙述正确的的有（ ）①对角线互相垂直的四边形是平行四边形；②两组对边分别相等的四边形是平行四边形；③一组对边平行，另一组对边相等的四边形是平行四边形．A．3个 B．2个 C．1个 D．0个
3. 下列图形中，一定可以拼成平行四边形的是(　　)A．两个等腰三角形 B．两个直角三角形C．两个锐角三角形 D．两个全等三角形
4.如图，在▱ABCD中，点E，F分别在AD，BC上，若要使四边形AFCE是平行四边形，可以添加的条件是(　　)①AF＝CF；②AE＝CE；③BF＝DE；④AF∥CE.A．①或②　 B．②或③ C．③或④　 D．①或③
5.如图，分别以△ABC的三边为一边，在BC的同侧作等边三角形ABD，等边三角形BCE，等边三角形ACF，连接DE，EF.求证：四边形ADEF是平行四边形．
证明：∵△ABD、△BCE、△ACF都为等边三角形，∴DB＝AB＝AD，BE＝BC，AC＝AF， ∠DBA＝60°，∠EBC＝60°.∴∠DBE＝60°－∠EBA，∠ABC＝60°－∠EBA，∴∠DBE＝∠ABC，∴△DBE≌△ABC，∴DE＝AC.又∵AC＝AF，∴AF＝DE.同理可证：△ABC≌△FEC，∴AB＝FE，∴FE＝AD，∴四边形ADEF是平行四边形．
6.如图,在四边形ABCD中,AB=CD,过点A作AE⊥BD交BD于点E,过点C作CF⊥BD交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.
证明:∵AE⊥BD,CF⊥BD,∴∠AEB=∠CFD=90°.在Rt△ABE和Rt△CDF中,∵AE=CF，AB=CD,∴Rt△ABE≌Rt△CDF,∴∠ABE=∠CDF,∴AB∥CD.∵AB=CD,∴四边形ABCD是平行四边形.
1、两组对边分别平行的四边形是平行四边形(定义)
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
“习题6.3”第1、2、3题