四川省阆中中学2024届高三上学期一模数学试题（理）（Word版附解析）

这是一份四川省阆中中学2024届高三上学期一模数学试题（理）（Word版附解析），共17页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

（满分：150分 考试时间：120分钟）
一、单选题。(每小题5分，共计60分)
1．已知集合，则（ ）
A．B．C．D．
2．已知，则（ ）
A．B．C．D．
3．在等比数列中，，，则（ ）
A．B．C．D．
4．若曲线在处的切线与直线垂直，则实数（ ）
A．1B．C．D．2
5．已知函数的部分图像如图，则函数的解析式可能为（ ）
A． B．
C． D．
6．已知向量满足，则与的夹角为（ ）
A．B．C．D．
7．设变量满足约束条件，则目标函数的最小值为（ ）
A．-8B．-15C．-20D．-21
8． 已知函数的最小正周期为T，若，且是
的一个极值点，则（ ）
A．B．2C．D．
9． 已知函数，则对任意非零实数x，有（ ）
A．B．
C．D．
10．圆O是边长为的等边三角形ABC的内切圆，其与BC边相切于点D，点M圆上
任意一点，（x，），则的最大值为（ ）
A．B．2C．D．
11．油纸伞是中国传统工艺品，至今已有1000多年的历史，为宣传
和推广这一传统工艺，北京市文化宫于春分时节开展油纸伞文
化艺术节.活动中将油纸伞撑开后摆放在户外展览场地上，如图
所示，该伞的伞沿是一个半径为的圆，圆心到伞柄底端距离
为，阳光照射油纸伞在地面形成了一个椭圆形影子（春分时，
北京的阳光与地面夹角为），若伞柄底端正好位于该椭圆的
焦点位置，则该椭圆的离心率为（ ）
A．B．C．D．
12．定义在上的奇函数满足，且在上单调递减，若方程
在上有实数根,则方程在区间上所有实根之和是（ ）
A．30B．14C．12D．6
二、填空题。（每小题5分，共计20分）
13．在某市的一次高三测试中，学生数学成绩X服从正态分布，已知，若按成绩分层抽样抽取100份试卷进行分析，其中120分以
上的试卷份数为 .
14．的展开式中的系数为 （用数字作答）．
15．点M是双曲线渐近线上一点，若以M为圆心的圆与圆C：x2+y2-4x+3=0
相切，则圆M的半径的最小值等于 .
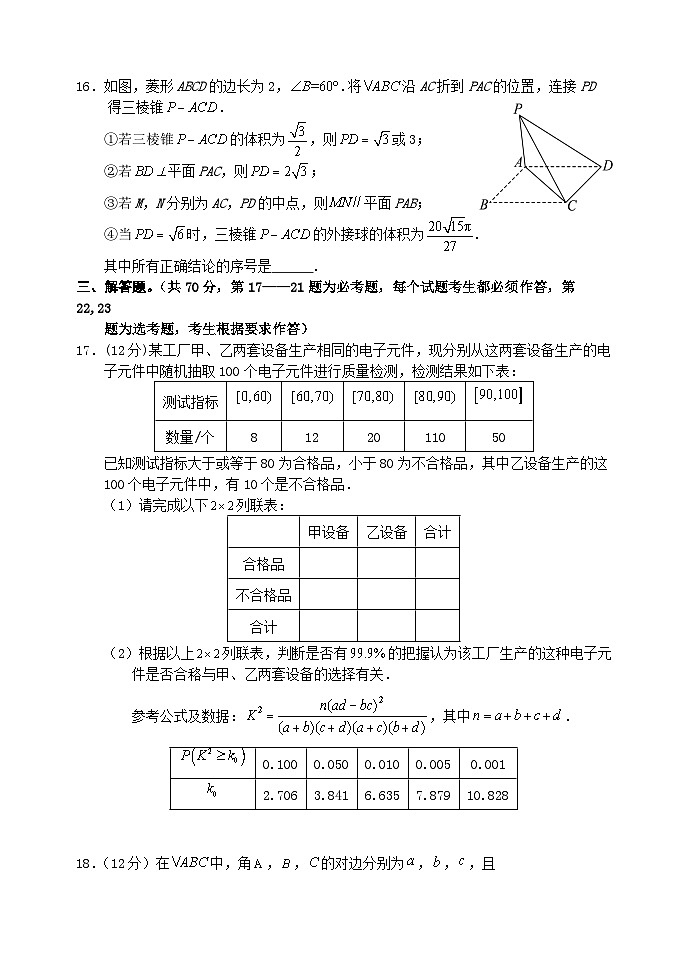
16．如图，菱形ABCD的边长为2，.将沿AC折到PAC的位置，连接PD
得三棱锥.
①若三棱锥的体积为，则或3；
②若平面PAC，则；
③若M，N分别为AC，PD的中点，则平面PAB；
④当时，三棱锥的外接球的体积为.
其中所有正确结论的序号是 .
三、解答题。（共70分，第17——21题为必考题，每个试题考生都必须作答，第22,23
题为选考题，考生根据要求作答）
17．(12分)某工厂甲、乙两套设备生产相同的电子元件，现分别从这两套设备生产的电
子元件中随机抽取100个电子元件进行质量检测，检测结果如下表：
已知测试指标大于或等于80为合格品，小于80为不合格品，其中乙设备生产的这100个电子元件中，有10个是不合格品．
（1）请完成以下列联表：
（2）根据以上列联表，判断是否有的把握认为该工厂生产的这种电子元
件是否合䅂与甲、乙两套设备的选择有关．
参考公式及数据：，其中．
18．（12分）在中，角，，的对边分别为，，，且.
（1）求；
（2）若点在边上，，，，求的面积.
19．（12分）如图，平面平面ABS，四边形ABCD为矩形，为正三角形，
，为AB的中点．

（1）证明：平面平面BDS；
（2）求二面角的正弦值．
20．（12分）已知斜率为的直线与抛物线相交于两点．
（1）求线段中点纵坐标的值；
（2）已知点，直线分别与抛物线相交于两点（异于）．
求证：直线恒过定点，并求出该定点的坐标．
21．（12分）已知函数.
（1）当时，求曲线在点处的切线方程；
（2）若，求实数a的取值范围.
22．（10分）在平面直角坐标系中，曲线的参数方程为（参数），
以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，曲线的极坐标方程为
，其中.
（1）求曲线与曲线的交点的极坐标；
（2）直线与曲线，分别交于M，N两点（异于极点O），P为
上的动点，求面积的最大值.
23．（10分）已知.
（1）当时，求不等式的解集；
（2）若时不等式成立，求的取值范围。
理科数学参考答案
1．C2．A3．D4．B5．B
6．B7．C8．D9．D
10．B
【详解】以D点为原点，BC所在直线为x轴，AD所在直线为y轴，建立坐标系，
因为圆O是边长为的等边三角形ABC的内切圆，
所以，即内切圆的圆心为，半径为1，
可设，又，
∴，，
∴，
故得到，
∴，
∴，
当时等号成立，即的最大值为2.
故选：B.
11．A
【详解】如图，伞的伞沿与地面接触点B是椭圆长轴的一个端点，伞沿在地面上最远的投影点A是椭圆长轴的另一个端点，
对应的伞沿为C，O为伞的圆心，F为伞柄底端，即椭圆的左焦点，令椭圆的长半轴长为，半焦距为，
由，得，，
在中，，则，，
由正弦定理得，，解得，则，
所以该椭圆的离心率.
故选：A
12．A
【详解】由知函数的图象关于直线对称，
∵，是R上的奇函数，
∴，
∴，
∴的周期为4，
考虑的一个周期，例如，
由在上是减函数知在上是增函数，
在上是减函数，在上是增函数，
对于奇函数有，，
故当时，，当时，，
当时，，当时，，
方程在上有实数根，
则这实数根是唯一的，因为在上是单调函数，
则由于，故方程在上有唯一实数，
在和上，
则方程在和上没有实数根，
从而方程在一个周期内有且仅有两个实数根，
当，方程的两实数根之和为，
当，方程的所有6个实数根之和为.
故选：A.
13．15
14．
15．
16．①③④
【详解】对于②，设，若平面PAC，平面PAC，所以.
因为菱形ABCD的边长为2，，所以是等边三角形，
所以,即.
因为,平面,所以平面.
因为平面，所以.
又，所以,故②错误.
对于④，由②可得当时，平面,
设为三棱锥的外接球球心，为等边的重心，过作,垂足为，
因为，所以,,
所以三棱锥的外接球半径为,
所以三棱锥的外接球体积为，故④正确.
对于①，设在的投影为，因为，所以在所在的直线上.
又，所以，解得.
因为二面角可能为锐角或钝角，
（i）当二面角为钝角时，
所以,，
所以.
（ii）当二面角为锐角时，
因为,，
所以在中，由余弦定理可得,
即，即,解得.
所以是的中点，所以,
所以.
综上，或3，故①正确.
对于③，若M，N分别为AC，PD的中点，由中位线定理可得,
因为平面,平面,
所以平面，故③正确.
故答案为:①③④.
17【详解】（1）如下表所示：
（2）因为，
所以有的把握认为该工厂生产的这种电子元件是否合格与甲、乙两套设备的选择有关．
18．(1)
(2)
【详解】（1）由题意得，
所以，故
因为，.
（2）设，则，
在中，有.
在中，有.
又，所以，
所以有.又，所以.
在中，由余弦定理可得.
又，，，
所以有.
联立，解得 ，所以，
所以.
19．(1)证明见解析
(2)
【详解】（1）证明：设BD与OC相交于点，
因为为正三角形，所以，
又为AB的中点，则．
因为平面平面ABS，平面ABS，平面平面，，所以平面ABCD，
又平面，则．
因为四边形ABCD为矩形，，
在中，，
在中，，
所以，所以，
又，则，即，所以，
又，，平面，所以平面SOC，
又平面BDS，所以平面平面BDS．
（2）解：因为四边形ABCD为矩形，所以，
又平面平面SAB，平面平面，平面ABCD，所以平面SAB．
以为坐标原点，过点作平行于AD的直线为轴，以OB和OS所在直线分别为轴和轴，建立如图所示的空间直角坐标系．

设，则，，，，，
，，，
设平面SCD的一个法向量为，
则，即，
令，则．
由（1）可知，平面SOC，所以是平面SOC的一个法向量．
因为，
所以二面角的正弦值为．
20．(1)
(2)证明见解析，定点的坐标为
【详解】（1）设，其中，
由，得，化简得，
，即，
线段中点纵坐标的值为；
（2）证明：设，
，
直线的方程为，化简可得，
在直线上，解得，
同理，可得，
，
，
又直线的方程为，即，
直线恒过定点．
21．(1)；
(2).
【详解】（1）当时，,则，
所以，即在点处的切线斜率为.
而，所以切点坐标为，
所以曲线在点处的切线方程为，即.
（2）因为，
所以，即，即.
令，则.
，所以在上单调递增，
所以恒成立，即，即恒成立.
令，则，
令，解得，令，解得,
所以在上单调递减，在上单调递增，
所以.
因为恒成立，所以，解得.
所以实数a的取值范围是.
22．(1)和
(2)
【详解】（1）的参数方程为（为参数），消去可得，
，所以曲线的直角坐标方程为.
将，代入得，曲线的极坐标方程为
的极坐标方程为，联立可得，
又因为两个曲线都经过极点，
所以曲线和曲线的交点极坐标为和.
（2）当时，，，.
显然当点P到直线MN的距离最大时，△PMN的面积最大，
直线MN的方程为，圆心到直线MN的距离为，
所以点P到直线MN的最大距离，
所以.
23．（1）；（2）．
【详解】（1）［方法一］：【通性通法】零点分段法
当时，，即，所以不等式等价于或或，解得：．
故不等式的解集为．
［方法二］：【最优解】数形结合法
如图，当时，不等式即为．
由绝对值的几何意义可知，表示x轴上的点到对应的点的距离减去到1对应点的距离．结合数轴可知，当时，，当时，．故不等式的解集为．
（2）［方法一］：【通性通法】分类讨论
当时，成立等价于当时，成立．
若，则当时，；
若，由得，，解得：，所以，故．
综上，的取值范围为．
［方法二］：平方法
当时，不等式成立，等价于时，成立，即成立，整理得．
当时，不等式不成立；
当时，，不等式解集为空集；
当时，原不等式等价于，解得．
由，解得．故a的取值范围为．
［方法三］：【最优解】分离参数法
当时，不等式成立，等价于时，成立，
即，解得：，而，所以．故a的取值范围为．测试指标
数量/个
8
12
20
110
50
甲设备
乙设备
合计
合格品
不合格品
合计
0.100
0.050
0.010
0.005
0.001
2.706
3.841
6.635
7.879
10.828
甲设备
乙设备
合计
合格品
70
90
160
不合格品
30
10
40
合计
100
100
200